以前写过关于一系列的博弈的论文,主要是现有一些博弈的结论和证明,可以参考链接。
关于SG定理以及NIM博弈可行性的证明,还有基础博弈的一些想法,可以参考张一飞前辈02年的国家集训队论文《由感性到理想认识-透析一类博弈游戏的解答过程》。
关于一些特殊思路的思考过程以及证明,可以参考王晓珂前辈02年的论文《解析一类组合游戏》。
还有贾志豪前辈的一些特殊SG游戏的归纳论证《组合游戏略述——浅谈SG游戏的若干拓展及变形》。
曹钦翔前辈对于博弈过程的一些推理方法以及技巧:《从“k倍动态减法游戏”出发探究一类组合游戏问题》。
1.POI 2000
Stripes
Time Limit:1000MSMemory Limit:30000KB
Total Submit:71Accepted:31
Description
Stripes is a two player game. Necessary requisites are a board and rectangular stripes in three colours: red, green and blue. All the red stripes have dimensions c x 1, green - z x 1, and blue - n x 1, where c, z and n are integers. Players have at their disposal an unlimited pool of stripes of each colour.
A game board is a rectangle of dimensions p x 1 and consists of p fields of size 1 x 1.
Players make their moves by turns. Move consists of laying a stripe of any colour on the board. There are the following rules in force:
A stripe cannot stick out of the board,
The covering (even partially) the earlier laid stripes is forbidden.
The ends of a stripe have to adhere to the edges of the fields on the board. The player, who is not able to perform his move in accordance to the game rules first, loses.
The first player is this one, who makes the first move in the game. It is said, that the first player has a winning strategy, if independently of the moves of the second player he can always win.
Task
Write a program, which:
1.reads sizes of stripes and of at least one board
2.for each board determines, whether the first player has a winning strategy,
3.writes the results.
Input
The first line of the input consists of three integers c, z and n, 1 <= c, z, n <= 1000, equal to the lengths of stripes, adequately: red, green and blue ones. Numbers in the line are separated by single spaces.
The second line of the file PAS.IN consists of one number m, 1 <= m <= 1000, which is equal to the number of different boards to consider. Lines from the 3-rd to the (m+2)-th consists of one number p, 1 <= p < 1000. Number in the (i+2)-th line is the length of the i-th board.
Output
The output should contain m lines. Only one number should be written in the i-th line of the file:
1 - if the first player has a winning strategy on the i-th board
2 - otherwise.
Sample Input
1 5 1
3
1
5
6
Sample Output
1
1
2
简单的应用,把每个子状态的SG函数计算出来就行了。

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<set> 5 #define clr(x) memset(x,0,sizeof(x)) 6 using namespace std; 7 int color[3]; 8 int sg[1010]; 9 void init() 10 { 11 for(int i=0;i<=1000;i++) 12 { 13 set<int> mex; 14 for(int j=0;j<3;j++) 15 for(int k=color[j];k<=i;k++) 16 { 17 int t=sg[k-color[j]]^sg[i-k]; 18 mex.insert(t); 19 } 20 for(int j=0;j<=1000;j++) 21 if(mex.find(j)==mex.end()) 22 { 23 dp[i]=j; 24 break; 25 } 26 } 27 28 } 29 int main() 30 { 31 while(scanf("%d",&color[0])!=EOF) 32 { 33 for(int i=1;i<3;i++) 34 scanf("%d",&color[i]); 35 clr(sg); 36 init(); 37 int t; 38 scanf("%d",&t); 39 while(t--) 40 { 41 int n; 42 scanf("%d",&n); 43 if(sg[n]==0) puts("2"); 44 else puts("1"); 45 } 46 } 47 return 0; 48 } 49 50
2.poj 1704
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 10301 | Accepted: 3382 |
Description
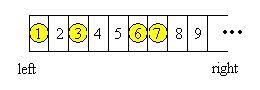
Georgia and Bob move the chessmen in turn. Every time a player will choose a chessman, and move it to the left without going over any other chessmen or across the left edge. The player can freely choose number of steps the chessman moves, with the constraint that the chessman must be moved at least ONE step and one grid can at most contains ONE single chessman. The player who cannot make a move loses the game.
Georgia always plays first since "Lady first". Suppose that Georgia and Bob both do their best in the game, i.e., if one of them knows a way to win the game, he or she will be able to carry it out.
Given the initial positions of the n chessmen, can you predict who will finally win the game?
Input
Output
Sample Input
2 3 1 2 3 8 1 5 6 7 9 12 14 17
Sample Output
Bob will win Georgia will win
简单应用,若为奇数个点则加上0位置变为偶数个点,然后相邻两个点作为一个点对,即有${a}_{1},{a}_{2},{a}_{3}……{a}_{n}$这些棋子,${a}_{i}$表示棋子位置。那么按照$({a}_{1},{a}_{2}),({a}_{3},{a}_{4})……({a}_{n-1},{a}_{n})$这样配对,以每对点对之间的间隔数作为石子堆数,那么就相当于一个nim博弈。

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<algorithm> 5 #define clr(x) memset(x,0,sizeof(x)) 6 int a[100001]; 7 using namespace std; 8 int main() 9 { 10 int t,n,m,p,sum; 11 scanf("%d",&n); 12 for(int k=0;k<n;k++) 13 { 14 scanf("%d",&m); 15 for(int i=0;i<m;i++) 16 scanf("%d",&a[i]); 17 if(m%2==1) 18 a[m++]=0; 19 sort(a,a+m); 20 sum=0; 21 for(int i=0;i<m/2;i++) 22 sum^=a[2*i+1]-a[2*i]-1; 23 if(sum==0) 24 printf("Bob will win "); 25 else 26 printf("Georgia will win "); 27 28 } 29 return 0; 30 31 }
3.poj 3537
| Time Limit: 3000MS | Memory Limit: 65536K | |
| Total Submissions: 3642 | Accepted: 1434 | |
| Case Time Limit: 2000MS | ||
Description
The game of Crosses and Crosses is played on the field of 1 × n cells. Two players make moves in turn. Each move the player selects any free cell on the field and puts a cross ‘×’ to it. If after the player’s move there are three crosses in a row, he wins.
You are given n. Find out who wins if both players play optimally.
Input
Input file contains one integer number n (3 ≤ n ≤ 2000).
Output
Output ‘1’ if the first player wins, or ‘2’ if the second player does.
Sample Input
3
6
Sample Output
1
2
对于最终状态xxx,固定第一个x,那么他有前驱状态x_x和xx_,也就是我们填入一个x后,对手尽可能地不会在其相邻(左和右)的两个格子内填入x,否则你就赢了。
那么我们可以将其转化为1维的每次操作能去掉连续5个棋子的nim游戏。那么长度为n的子状态为$g(n)={(i-3,n-i,2)},i∈(1,n)$对于小于0的状态将其当做0状态,因为这状态肯定终止了。

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #define clr(x) memset(x,0,sizeof(x)) 5 using namespace std; 6 int sg[2010],n,m,k,p; 7 bool inf[2010]; 8 int above(int i) 9 { 10 return i>0?i:0; 11 } 12 int main() 13 { 14 sg[0]=0; 15 for(int i=1;i<=2000;i++) 16 { 17 clr(inf); 18 for(int j=1;j<=i;j++) 19 { 20 p=sg[above(j-3)]^sg[above(i-j-2)]; 21 inf[p]=1; 22 } 23 for(int j=0;;j++) 24 if(inf[j]==0) 25 { 26 sg[i]=j; 27 break; 28 } 29 } 30 while(scanf("%d",&n)!=EOF) 31 { 32 if(sg[n]==0) 33 printf("2 "); 34 else 35 printf("1 "); 36 } 37 return 0; 38 39 }
4.POJ 3710
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 2268 | Accepted: 715 |
Description
Harry and Sally were playing games at Christmas Eve. They drew some Christmas trees on a paper:
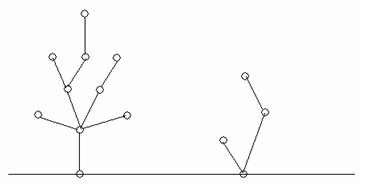
Then they took turns to cut a branch of a tree, and removed the part of the tree which had already not connected with the root. A step shows as follows:
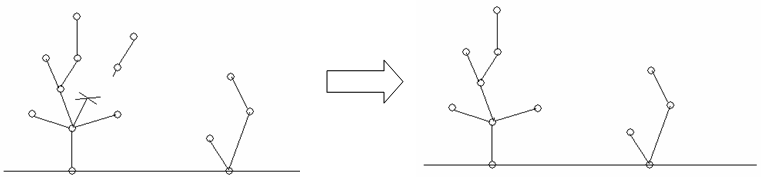
Sally always moved first. Who removed the last part of the trees would win the game.
After a while, they all figured out the best strategy and thought the game was too simple for them. Harry said, “The Christmas trees should have some gifts in them!” So Sally drew some gifts (simple polygons) in the initial trees:
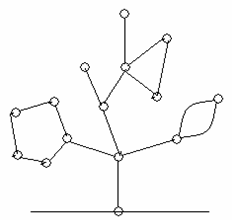
You may assume the initial picture is a tree with some simple polygons, in which each edge is involved in at most one polygon. We also know that every polygon has only one node involved in the main tree (the hanging point of the giftJ) .In every sub-tree (connected subgraph), there was one and only one node representing the “root”. According to these assumptions, following graphs will never appear:
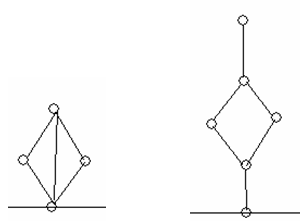
Sally and Harry took turns (Sally was always the first person to move), to cut an edge in the graph, and removed the part of the tree that no longer connected to the root. The person who cannot make a move lost the game.
Your job is to decide who will finally win the game if both of them use the best strategy.
Input
The input file contains multiply test cases.
The first line of each test case is an integer N (N<100), which represents the number of sub-trees. The following lines show the structure of the trees. The first line of the description of a tree is the number of the nodes m (m<100) and the number of the edges k (k<500). The nodes of a tree are numbered from 1 to m. Each of following lines contains 2 integers a and b representing an edge <a, b>. Node 1 is always the root.
Output
For each test case, output the name of the winner.
Sample Input
2 2 1 1 2 4 4 1 2 2 3 2 4 3 4
Sample Output
Sally
这题就是树上博弈,然后我用tarjan把环缩点,其中偶数环缩成一个点,奇数环缩成一个点加一条边(Fusion Principle)。因为tarjan判的是有向图,所以我们做无向图缩点的时候,假设我们从节点fa递归到子节点x,然后我们不能在节点x tarjan的时候遍历相邻节点的时候再次访问fa(因为是无向图嘛所以双向建边),所以我们要记录前驱节点pre,然后防止前驱节点被后继节点再次访问。这样就完成无向图的缩点了。
然后缩完点以后就按照树上删边游戏的做法去做就行了。

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #define clr(x) memset(x,0,sizeof(x)) 5 #define clr_1(x) memset(x,-1,sizeof(x)) 6 using namespace std; 7 struct edg 8 { 9 int to,next; 10 }edge[2][100010]; 11 int belong[20010],sta[20010],head[2][20010],low[20010],dfn[20010],sg[20010]; 12 bool instack[20010]; 13 int n,m,k,l,r,s,t,cnt,all,top,elem,clock; 14 int min(int a,int b) 15 { 16 return a<b?a:b; 17 } 18 void addedge(int t,int u,int v) 19 { 20 edge[t][++cnt].to=v; 21 edge[t][cnt].next=head[t][u]; 22 head[t][u]=cnt; 23 return ; 24 } 25 void init() 26 { 27 t^=1; 28 all=elem; 29 clr(low); 30 clr(dfn); 31 clr(instack); 32 elem=1; 33 clock=top=0; 34 return ; 35 } 36 void tarjan(int t,int pre,int x) 37 { 38 dfn[x]=low[x]=++clock; 39 sta[++top]=x; 40 instack[x]=1; 41 int p; 42 for(int i=head[t][x];i!=-1;i=edge[t][i].next) 43 { 44 p=edge[t][i].to; 45 if(p==pre) 46 continue; 47 if(!dfn[p]) 48 { 49 tarjan(t,x,p); 50 low[x]=min(low[x],low[p]); 51 } 52 else if(instack[p]) 53 { 54 low[x]=min(low[x],dfn[p]); 55 } 56 } 57 if(low[x]==dfn[x]) 58 { 59 bool flag=0; 60 if(instack[1]) 61 { 62 flag=1; 63 } 64 elem++; 65 int m=top; 66 do 67 { 68 belong[sta[top]]=elem; 69 instack[sta[top]]=0; 70 top--; 71 } 72 while(sta[top+1]!=x); 73 if(flag==1 && instack[1]==0) 74 { 75 for(int i=top+1;i<=m;i++) 76 { 77 belong[sta[i]]=1; 78 } 79 elem--; 80 } 81 m-=top; 82 if(m!=1 && m%2==1) 83 { 84 all++; 85 addedge(t,x,all); 86 addedge(t,all,x); 87 belong[all]=++elem; 88 } 89 } 90 return ; 91 } 92 void shrink(int t,int n) 93 { 94 int p; 95 clr_1(head[t^1]); 96 cnt=0; 97 for(int i=1;i<=n;i++) 98 { 99 for(int j=head[t][i];j!=-1;j=edge[t][j].next) 100 { 101 p=edge[t][j].to; 102 if(belong[i]!=belong[p]) 103 { 104 addedge(t^1,belong[i],belong[p]); 105 } 106 } 107 } 108 return ; 109 } 110 void dfs(int t,int pre,int i) 111 { 112 sg[i]=0; 113 int p; 114 for(int j=head[t][i];j!=-1;j=edge[t][j].next) 115 { 116 p=edge[t][j].to; 117 if(p!=pre) 118 { 119 dfs(t,i,p); 120 sg[i]^=(sg[p]+1); 121 } 122 } 123 return ; 124 } 125 int main() 126 { 127 while(scanf("%d",&k)!=EOF) 128 { 129 all=1; 130 cnt=0; 131 clr_1(head[0]); 132 for(int i=1;i<=k;i++) 133 { 134 scanf("%d%d",&n,&m); 135 for(int i=1;i<=m;i++) 136 { 137 scanf("%d%d",&l,&r); 138 if(l!=1) 139 l=all+l-1; 140 if(r!=1) 141 r=all+r-1; 142 addedge(0,l,r); 143 addedge(0,r,l); 144 } 145 all+=n-1; 146 } 147 elem=all; 148 t=1; 149 do 150 { 151 init(); 152 tarjan(t,0,1); 153 shrink(t,all); 154 } 155 while(elem<all); 156 t^=1; 157 dfs(t,1,1); 158 if(sg[1]) 159 { 160 printf("Sally "); 161 } 162 else 163 { 164 printf("Harry "); 165 } 166 } 167 return 0; 168 }
5.poj 2068
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 1803 | Accepted: 1018 |
Description
In this game, you have a winning strategy. To see this, you first remove four stones and leave 96 stones. No matter how I play, I will end up with leaving 92 - 95 stones. Then you will in turn leave 91 stones for me (verify this is always possible). This way, you can always leave 5k+1 stones for me and finally I get the last stone, sigh. If we initially had 101 stones, on the other hand, I have a winning strategy and you are doomed to lose.
Let's generalize the game a little bit. First, let's make it a team game. Each team has n players and the 2n players are seated around the table, with each player having opponents at both sides. Turn around the table so the two teams play alternately. Second, let's vary the maximum number of stones each player can take. That is, each player has his/her own maximum number of stones he/she can take at each turn (The minimum is always one). So the game is asymmetric and may even be unfair.
In general, when played between two teams of experts, the outcome of a game is completely determined by the initial number of stones and the maximum number of stones each player can take at each turn. In other words, either team has a winning strategy.
You are the head-coach of a team. In each game, the umpire shows both teams the initial number of stones and the maximum number of stones each player can take at each turn. Your team plays first. Your job is, given those numbers, to instantaneously judge whether your team has a winning strategy.
Incidentally, there is a rumor that Captain Future and her officers of Hakodate-maru love this game, and they are killing their time playing it during their missions. You wonder where the stones are? Well, they do not have stones but do have plenty of balls in the fuel containers!
Input
n S M1 M2 . . . M2n
where n is the number of players in a team, S the initial number of stones, and Mi the maximum number of stones ith player can take. 1st, 3rd, 5th, ... players are your team's players and 2nd, 4th, 6th, ... the opponents. Numbers are separated by a single space character. You may assume 1 <= n <= 10, 1 <= Mi <= 16, and 1 <= S < 2^13.
Output
Sample Input
1 101 4 4 1 100 4 4 3 97 8 7 6 5 4 3 0
Sample Output
0 1 1
总的来说是一道水题,看看数据范围就知道了。
反正从1开始对每个石子数,每个人都计算下他的胜负状况,能转移到p状态的是n状态,否则为p状态。

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #define clr(x) memset(x,0,sizeof(x)) 5 using namespace std; 6 int dp[30][10010],maxn[30]; 7 int max(int a,int b) 8 { 9 return a>b?a:b; 10 } 11 int main() 12 { 13 int n,m,s; 14 while(scanf("%d",&n)!=EOF && n!=0) 15 { 16 scanf("%d",&s); 17 n<<=1; 18 for(int i=1;i<=n;i++) 19 { 20 scanf("%d",&maxn[i]); 21 dp[i][0]=1; 22 } 23 for(int i=1;i<=s;i++) 24 { 25 for(int j=1;j<=n;j++) 26 { 27 dp[j][i]=0; 28 for(int k=max(0,i-maxn[j]);k<i;k++) 29 { 30 if(dp[(j)%n+1][k]==0) 31 { 32 dp[j][i]=1; 33 break; 34 } 35 } 36 37 } 38 } 39 if(dp[1][s]==1) 40 printf("1 "); 41 else 42 printf("0 "); 43 } 44 return 0; 45 }
6.poj 2975[hdu 1850]
Descriptio
Nim is a 2-player game featuring several piles of stones. Players alternate turns, and on his/her turn, a player’s move consists of removing one or more stones from any single pile. Play ends when all the stones have been removed, at which point the last player to have moved is declared the winner. Given a position in Nim, your task is to determine how many winning moves there are in that position.
A position in Nim is called “losing” if the first player to move from that position would lose if both sides played perfectly. A “winning move,” then, is a move that leaves the game in a losing position. There is a famous theorem that classifies all losing positions. Suppose a Nim position contains n piles having k1, k2, …, kn stones respectively; in such a position, there are k1 + k2 + … +kn possible moves. We write each ki in binary (base 2). Then, the Nim position is losing if and only if, among all the ki’s, there are an even number of 1’s in each digit position. In other words, the Nim position is losing if and only if the xor of the ki’s is 0.
Consider the position with three piles given by k1 = 7, k2 = 11, and k3 = 13. In binary, these values are as follows:
111
1011
1101
There are an odd number of 1’s among the rightmost digits, so this position is not losing. However, suppose k3 were changed to be 12. Then, there would be exactly two 1’s in each digit position, and thus, the Nim position would become losing. Since a winning move is any move that leaves the game in a losing position, it follows that removing one stone from the third pile is a winning move when k1 = 7, k2 = 11, and k3 = 13. In fact, there are exactly three winning moves from this position: namely removing one stone from any of the three piles.
Input
The input test file will contain multiple test cases, each of which begins with a line indicating the number of piles, 1 ≤ n ≤ 1000. On the next line, there are n positive integers, 1 ≤ ki ≤ 1, 000, 000, 000, indicating the number of stones in each pile. The end-of-file is marked by a test case with n = 0 and should not be processed.
Output
For each test case, write a single line with an integer indicating the number of winning moves from the given Nim position.
Sample Input
3 7 11 13 2 1000000000 1000000000 0
Sample Output
3 0
首先,全部堆异或一下求个异或和ans,若果为0直接输出0退出。
如果不为0,那么能取的堆p就是一开始所有堆都在的时候,取该堆p以后能转移到异或和为0的平衡态的状态。因此若没有堆p时的异或和t小于p的石子数s[p],那么我们就可以将该堆由s[p]取到t,使得异或和为0转移到平衡态,那么这个堆就是可取的,加入答案中。

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #define clr(x) memset(x,0,sizeof(x)) 5 #define LL long long 6 using namespace std; 7 LL pile[10010]; 8 LL max(LL a,LL b) 9 { 10 return a>b?a:b; 11 } 12 int main() 13 { 14 int n,k,l; 15 LL ans; 16 while(scanf("%d",&n)!=EOF && n!=0) 17 { 18 ans=0; 19 k=0; 20 for(int i=1;i<=n;i++) 21 { 22 scanf("%d",&pile[i]); 23 ans^=pile[i]; 24 } 25 if(ans==0) 26 { 27 printf("0 "); 28 continue; 29 } 30 for(int i=1;i<=n;i++) 31 { 32 if((ans^pile[i])<=pile[i]) 33 k++; 34 } 35 printf("%d ",k); 36 } 37 return 0; 38 } 39
7.hdu 1079
Calendar Game
A player wins the game when he/she exactly reaches the date of November 4, 2001. If a player moves to a date after November 4, 2001, he/she looses the game.
Write a program that decides whether, given an initial date, Adam, the first mover, has a winning strategy.
For this game, you need to identify leap years, where February has 29 days. In the Gregorian calendar, leap years occur in years exactly divisible by four. So, 1993, 1994, and 1995 are not leap years, while 1992 and 1996 are leap years. Additionally, the years ending with 00 are leap years only if they are divisible by 400. So, 1700, 1800, 1900, 2100, and 2200 are not leap years, while 1600, 2000, and 2400 are leap years.
打表题

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #define clr(x) memset(x,0,sizeof(x)) 5 int day[2002040]; 6 int month[2][13]={{0,31,29,31,30,31,30,31,31,30,31,30,31},{0,31,28,31,30,31,30,31,31,30,31,30,31}}; 7 void init() 8 { 9 int y,m,d,all,next; 10 day[1011104]=0; 11 int limit=1011104; 12 for(int i=2001;i>=1900;i--) 13 if((i%100==0 && i%400==0)|| (i%100!=0 && i%4==0)) 14 { 15 for(int j=12;j>=1;j--) 16 for(int k=month[0][j];k>=1;k--) 17 { 18 all=(i-1900)*10000+j*100+k; 19 if(all>limit) 20 continue; 21 y=i; 22 m=j; 23 d=k; 24 m++; 25 if(m>12) 26 { 27 y++; 28 m=1; 29 } 30 next=(y-1900)*10000+m*100+d; 31 if(next<=limit && month[0][m]>=d) 32 { 33 if(day[next]==0) 34 day[all]=1; 35 } 36 y=i; 37 m=j; 38 d=k; 39 d++; 40 if(d>month[0][m]) 41 { 42 m++; 43 d=1;; 44 } 45 if(m>12) 46 { 47 y++; 48 m=1; 49 } 50 next=(y-1900)*10000+m*100+d; 51 if(next<=limit) 52 { 53 if(day[next]==0) 54 day[all]=1; 55 } 56 } 57 } 58 else 59 for(int j=12;j>=1;j--) 60 for(int k=month[1][j];k>=1;k--) 61 { 62 all=(i-1900)*10000+j*100+k; 63 day[all]=0; 64 if(all>limit) 65 continue; 66 y=i; 67 m=j; 68 d=k; 69 m++; 70 if(m>12) 71 { 72 y++; 73 m=1; 74 } 75 next=(y-1900)*10000+m*100+d; 76 if(next<=limit && month[1][m]>=d) 77 { 78 if(day[next]==0) 79 day[all]=1; 80 } 81 y=i; 82 m=j; 83 d=k; 84 d++; 85 if(d>month[1][m]) 86 { 87 m++; 88 d=1;; 89 } 90 if(m>12) 91 { 92 y++; 93 m=1; 94 } 95 next=(y-1900)*10000+m*100+d; 96 if(next<=limit) 97 { 98 if(day[next]==0) 99 day[all]=1; 100 } 101 } 102 } 103 int main() 104 { 105 init(); 106 int y,m,d,T,all; 107 scanf("%d",&T); 108 while(T--) 109 { 110 scanf("%d%d%d",&y,&m,&d); 111 all=(y-1900)*10000+m*100+d; 112 if(day[all]==1) 113 printf("YES "); 114 else 115 printf("NO "); 116 } 117 return 0; 118 }
8.hdu 1525
Euclid's Game
Problem Description
有两个玩家,Stan 和 Ollie, 在玩游戏。初始有两个自然数。Stan是先手,每次把大的数字减去小的数字的任意倍数,但是不能使数字变成负数。然后Ollie进行同样的操作,直到有一个玩家使一个数字变为零。
例如,初始时数字为(25,7):
25 7
11 7
4 7
4 3
1 3
1 0
这样Stan赢
Input
输入数据包含多行,每行两个正整数
Output
对于每组数据,加入先手赢,输出Stan wins,否则输出Ollie wins。最后一行为0 0,这一行不要处理
Sample Input
34 12 15 24 0 0
Sample Output
Stan wins Ollie wins
水题。。
设a为较大数。
初始为(a,b)这样一个状态,规定较大数在前。
若a%b==0,那当前操作者能取到0,获胜。
若a>2*b,那么由于当前操作者知道(b,a%b)是p还是n状态,那么若是n状态先手直接转移到(b,a%b),若是p状态则转移到(a%b+b,b)状态,当前操作者必胜。
若a<2*b,那么每次就只能老老实实地转移到(b,a%b)这个状态,这时候记录下当前操作者是谁,直到出现以上两种状况时,当前操作者获胜。

1 #include<cstdio> 2 #include<iostream> 3 #include<cstdlib> 4 using namespace std; 5 int main() 6 { 7 int a,b,t,p,man; 8 while(scanf("%d%d",&a,&b)&& a!=0) 9 { 10 int f=1; 11 while(1) 12 { 13 if(a>b) 14 swap(a,b); 15 if(b%a==0) 16 break; 17 if(b>2*a) 18 break; 19 b-=a; 20 f=1^f; 21 } 22 if(f) 23 printf("Stan wins "); 24 else 25 printf("Ollie wins "); 26 27 } 28 return 0; 29 }
9.hdu 1564
Play a game
ailyanlu is very happy today! and he is playing a chessboard game with 8600.
The size of the chessboard is n*n. A stone is placed in a corner square. They play alternatively with 8600 having the first move. Each time, player is allowed to move the stone to an unvisited neighbor square horizontally or vertically. The one who can't make a move will lose the game. If both play perfectly, who will win the game?
The integers are between 1 and 10000, inclusive,(means 1 <= n <= 10000) indicating the size of the chessboard. The end of the input is indicated by a zero.
No other characters should be inserted in the output.
水题,判奇偶。

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<string> 5 #define clr(x) memset(x,0,sizeof(x)) 6 using namespace std; 7 int main() 8 { 9 int n; 10 while(scanf("%d",&n) && n>0) 11 { 12 if(n%2==0) 13 printf("8600 "); 14 else 15 printf("ailyanlu "); 16 } 17 return 0; 18 }
10. hdu 1846
Brave Game
今天,大家选择上机考试,就是一种勇敢(brave)的选择;这个短学期,我们讲的是博弈(game)专题;所以,大家现在玩的也是“勇敢者的游戏”,这也是我命名这个题目的原因。
当然,除了“勇敢”,我还希望看到“诚信”,无论考试成绩如何,希望看到的都是一个真实的结果,我也相信大家一定能做到的~
各位勇敢者要玩的第一个游戏是什么呢?很简单,它是这样定义的:
1、 本游戏是一个二人游戏;
2、 有一堆石子一共有n个;
3、 两人轮流进行;
4、 每走一步可以取走1…m个石子;
5、 最先取光石子的一方为胜;
如果游戏的双方使用的都是最优策略,请输出哪个人能赢。
每组测试数据占一行,包含两个整数n和m(1<=n,m<=1000),n和m的含义见题目描述。
bash博弈

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<string> 5 #define clr(x) memset(x,0,sizeof(x)) 6 using namespace std; 7 int main() 8 { 9 int n,T,m; 10 scanf("%d",&T); 11 while(T--) 12 { 13 scanf("%d%d",&n,&m); 14 if(n%(m+1)==0) 15 printf("second "); 16 else 17 printf("first "); 18 } 19 return 0; 20 }
11.hdu 1847
Good Luck in CET-4 Everybody!
“升级”?“双扣”?“红五”?还是“斗地主”?
当然都不是!那多俗啊~
作为计算机学院的学生,Kiki和Cici打牌的时候可没忘记专业,她们打牌的规则是这样的:
1、 总共n张牌;
2、 双方轮流抓牌;
3、 每人每次抓牌的个数只能是2的幂次(即:1,2,4,8,16…)
4、 抓完牌,胜负结果也出来了:最后抓完牌的人为胜者;
假设Kiki和Cici都是足够聪明(其实不用假设,哪有不聪明的学生~),并且每次都是Kiki先抓牌,请问谁能赢呢?
当然,打牌无论谁赢都问题不大,重要的是马上到来的CET-4能有好的状态。
Good luck in CET-4 everybody!
mod 3 为0 后手赢。

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #define clr(x) memset(x,0,sizeof(x)) 5 using namespace std; 6 int main() 7 { 8 int n,m; 9 while(scanf("%d",&n)!=EOF) 10 { 11 if(n%3==0) 12 printf("Cici "); 13 else 14 printf("Kiki "); 15 } 16 return 0; 17 }
12.hdu 2516
取石子游戏
参看Sample Output.
2倍动态减法游戏,斐波那契博弈。

1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 using namespace std; 5 long long a[1000]={0}; 6 int main() 7 { 8 a[1]=1; 9 a[2]=1; 10 int k,l,j; 11 long long p=pow(2,31); 12 for( k=3;a[k-1]<=p;k++) 13 a[k]=a[k-1]+a[k-2]; 14 k--; 15 while(scanf("%d",&l) && l!=0) 16 { 17 for( j=1;j<=k;j++) 18 { 19 if(a[j]>l) 20 { 21 printf("First win "); 22 break; 23 } 24 if(a[j]==l) 25 { 26 printf("Second win "); 27 break; 28 } 29 } 30 } 31 return 0; 32 }
13.2897
邂逅明下
那天,日月相会,我见到了你。而且,大地失去了光辉,你我是否成侣?这注定是个凄美的故事。(以上是废话)
小t和所有世俗的人们一样,期待那百年难遇的日食。驻足街头看天,看日月渐渐走近,小t的脖子那个酸呀(他坚持这个姿势已经有半个多小时啦)。他低下仰起的头,环顾四周。忽然发现身边竟站着位漂亮的mm。天渐渐暗下,这mm在这街头竟然如此耀眼,她是天使吗?站着小t身边的天使。
小t对mm惊呼:“缘分呐~~”。mm却毫不含糊:“是啊,500年一遇哦!”(此后省略5000字….)
小t赶紧向mm要联系方式,可mm说:“我和你玩个游戏吧,赢了,我就把我的手机号告诉你。”小t,心想天下哪有题目能难倒我呢,便满口答应下来。mm开始说游戏规则:“我有一堆硬币,一共7枚,从这个硬币堆里取硬币,一次最少取2枚,最多4枚,如果剩下少于2枚就要一次取完。我和你轮流取,直到堆里的硬币取完,最后一次取硬币的算输。我玩过这个游戏好多次了,就让让你,让你先取吧~”
小t掐指一算,不对呀,这是不可能的任务么。小t露出得意的笑:“还是mm优先啦,呵呵~”mm霎时愣住了,想是对小t的反应出乎意料吧。
她却也不生气:“好小子,挺聪明呢,要不这样吧,你把我的邮箱给我,我给你发个文本,每行有三个数字n,p,q,表示一堆硬币一共有n枚,从这个硬币堆里取硬币,一次最少取p枚,最多q枚,如果剩下少于p枚就要一次取完。两人轮流取,直到堆里的硬币取完,最后一次取硬币的算输。对于每一行的三个数字,给出先取的人是否有必胜策略,如果有回答WIN,否则回答LOST。你把对应的答案发给我,如果你能在今天晚上8点以前发给我正确答案,或许我们明天下午可以再见。”
小t二话没说,将自己的邮箱给了mm。当他兴冲冲得赶回家,上网看邮箱,哇!mm的邮件已经到了。他发现文本长达100000行,每行的三个数字都很大,但是都是不超过65536的整数。小t看表已经下午6点了,要想手工算出所有结果,看来是不可能了。你能帮帮他,让他再见到那个mm吗?
可以发觉,对任意石子数n,n=k*(p+q)+t(t<=p,k∈Z),先手输,n=k*(p+q)+t(p<t<=q,k∈Z),先手赢。

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<string> 5 #define clr(x) memset(x,0,sizeof(x)) 6 using namespace std; 7 int main() 8 { 9 int n,p,q; 10 while(scanf("%d%d%d",&n,&p,&q)!=EOF) 11 { 12 n-=p; 13 if(n<=0) 14 { 15 printf("LOST "); 16 continue; 17 } 18 n=(n-1)%(p+q)+1; 19 if(n<=q) 20 printf("WIN "); 21 else 22 printf("LOST "); 23 } 24 return 0; 25 }
14.hdu 3032
Nim or not Nim?
Nim is usually played as a misere game, in which the player to take the last object loses. Nim can also be played as a normal play game, which means that the person who makes the last move (i.e., who takes the last object) wins. This is called normal play because most games follow this convention, even though Nim usually does not.
Alice and Bob is tired of playing Nim under the standard rule, so they make a difference by also allowing the player to separate one of the heaps into two smaller ones. That is, each turn the player may either remove any number of objects from a heap or separate a heap into two smaller ones, and the one who takes the last object wins.
这题是对sg函数的一个应用,在取石子的操作下多了分堆操作。这会导致sg函数产生什么样的改变呢?
我们把一个数转化为二进制来看。当这个数至多有一个数位1时,无论怎么分堆两个数异或和都会小于等于1,那么他的sg跟nim是一样的。
而当这个数有多个为1的数位时,那么一定至少一种方案分堆后异或和等于该数本身,那么他的sg为该数n+1。
而这样的改变带来的整体sg的变化是什么样的呢。
我们从0开始看起。
sg(0),sg(1),sg(2)为原nim的sg,因为他们至多一个1的数位,而3则有两个1的数位,所以3的mex里加入3本身,那么sg(3)=4。而sg(4)=mex{sg(0),sg(1),sh(2),sg(3),sg(sg(1)^sg(3)),sg(sg(2)^sg(2))}=mex{0,1,2,4,5,4}=3。所以sg(4)=3。
其实最实际的是打个表,你会发现sg(i%4==0)=i-1,sg(i%4==3)=i+1,sg(其他)=i。
然后通过数学归纳法可以得出上面的想法是正确的。

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<string> 5 #define clr(x) memset(x,0,sizeof(x)) 6 #define LL long long 7 using namespace std; 8 int main() 9 { 10 int T,n,m,p,q; 11 LL sum; 12 scanf("%d",&T); 13 while(T--) 14 { 15 scanf("%d",&n); 16 sum=0; 17 for(int i=1;i<=n;i++) 18 { 19 scanf("%d",&m); 20 p=m; 21 if(m%4==0) 22 p--; 23 else if(m%4==3) 24 p++; 25 if(p<0) 26 p=0; 27 sum^=p; 28 } 29 if(sum!=0) 30 printf("Alice "); 31 else 32 printf("Bob "); 33 } 34 return 0; 35 }
15.hdu 3389
Game
一开始我也没什么头绪,后来想到有移动石子这样的操作,一定跟阶梯博弈有什么必然的联系。
然后我们可以发觉1,3,4这三个位置的box是不能再往下移的了,换言之,就是最终状态,对应阶梯博弈的0号阶梯。
我们先考察1及他的所有前驱状态的位置形成的数列,我们可以发觉是这样的数列,1,2,7,8,13,14,19,20......6k+1,6k+2。
而3的数列为3,6,9......3k。
4的数列为4,5,10,11,16,17......6k+4,6k+5。
我们可以发现这三个数列交集为空集,并集为所有正整数。
那么每个数列就是一个封闭的数列,每个数ai对应i号阶梯(i>=0)。那么按照规则,每个数列里面奇数号阶梯的卡牌只能转移到偶数号阶梯上,偶数号阶梯上的卡牌只能转移到奇数号上,是一个广义的阶梯博弈,但做法依旧相同,那么就是把三个阶梯博弈的所有奇数堆异或下,然后再将三个异或和异或下之后判是否非0。
那么哪些数不需要异或呢,自己稍微总结下就是6k+1,6k+3,6k+4这样的位置为偶数编号阶梯,是没有异或到的。
那么边读边异或,就能得出最后的结果。
(代码为没有后续操作的23333当初没想到这个)

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #define clr(x) memset(x,0,sizeof(x)) 5 using namespace std; 6 int tag[3][10010],cnt[3],a[10010]; 7 void init(int n) 8 { 9 clr(tag); 10 clr(cnt); 11 for(int i=1;i<=n;i++) 12 if(i%6==1 || i%6==2) 13 { 14 tag[0][cnt[0]++]=i; 15 } 16 else if(i%6==3 || i%6==0) 17 { 18 tag[1][cnt[1]++]=i; 19 } 20 else 21 { 22 tag[2][cnt[2]++]=i; 23 } 24 return ; 25 } 26 int main() 27 { 28 init(10000); 29 int T,n,m,sum,kase=0; 30 scanf("%d",&T); 31 while(T--) 32 { 33 printf("Case %d: ",++kase); 34 scanf("%d",&n); 35 for(int i=1;i<=n;i++) 36 scanf("%d",&a[i]); 37 sum=0; 38 for(int i=0;i<3;i++) 39 { 40 for(int j=1;j<cnt[i] && tag[i][j]<=n;j+=2) 41 { 42 sum^=a[tag[i][j]]; 43 } 44 } 45 if(sum==0) 46 printf("Bob "); 47 else 48 printf("Alice "); 49 } 50 return 0; 51 }
16. hdu3537
Daizhenyang's Coin
In this game, n coins are set in a row, where n is smaller than 10^8. They took turns to flip coins, to flip one coin from head-up to tail-up or the other way around. Each turn, one can choose 1, 2 or 3 coins to flip, but the rightmost selected must be head-up before flipping operation. If one cannot make such a flip, he lost.
As we all know, Daizhenyang is a very smart guy (He's famous for his 26 problems and Graph Theory Unified Theory-Network Flow does it all ). So he will always choose the optimal strategy to win the game. And it's a very very bad news for all the competitors.
But the girl did not want to see that happen so easily, because she's not sure about her feelings towards him. So she wants to make Daizhenyang lose this game. She knows Daizhenyang will be the first to play the game. Your task is to help her determine whether her arrangement is a losable situation for Daizhenyang.
For simplicity, you are only told the position of head-up coins. And due to the girl's complicated emotions, the same coin may be described twice or more times. The other coins are tail-up, of course.
Coins are numbered from left to right, beginning with 0.

1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define LL long long 4 using namespace std; 5 bool infer(LL x) 6 { 7 int s=0; 8 while(x) 9 { 10 if(x&1) 11 { 12 s++; 13 } 14 x>>=1; 15 } 16 if(s&1) 17 return 1; 18 else 19 return 0; 20 } 21 map<LL,bool> num; 22 int main() 23 { 24 int n,T,k,l; 25 LL sum,m; 26 while(scanf("%d",&n)!=EOF) 27 { 28 num.erase(num.begin(),num.end()); 29 sum=0; 30 for(int i=1;i<=n;i++) 31 { 32 scanf("%lld",&m); 33 if(num[m]==1) 34 continue; 35 num[m]=1; 36 if(infer(m)) 37 sum^=2*m; 38 else 39 sum^=2*m+1; 40 } 41 if(sum==0) 42 printf("Yes "); 43 else 44 printf("No "); 45 } 46 return 0; 47 }
17.hdu3544
Alice's Game
Specifically, for Alice, a chocolate Xi * Yi, can only split into A * Yi, and B * Yi where A + B = Xi and A, B > 0. And for Bob, a chocolate Xi * Yi, can only split into Xi * A, and Xi * B where A + B = Yi and A, B > 0.
Alice and Bob are clever enough to take the optimal operation, if Alice plays first, your are to decide who will win.
For each test case, the first line contains an integer N, the number of pieces of chocolates. (1 <= N <= 100)
For the next N lines, each line contains two integers Xi and Yi, denoting the chocolate sized Xi * Yi. (1 <= Xi, Yi <= 1000000000)
一个不对称博弈,那我们的目标就是要尽可能地减少对手的切巧克力次数(因为我们切巧克力次数由对手操作决定,所以不可能增加自己的),所以尽量选则切得平均点。
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | -10 | -11 | -12 | -13 | -14 | -15 |
| 2 | 1 | 0 | 0 | -1 | -1 | -2 | -2 | -3 | -3 | -4 | -4 | -5 | 5 | -6 | -6 | -7 |
| 3 | 2 | 0 | 0 | -1 | -1 | -2 | -2 | -3 | -3 | -4 | -4 | -5 | 5 | -6 | -6 | -7 |
| 4 | 3 | 1 | 1 | 0 | 0 | 0 | 0 | -1 | -1 | -1 | -1 | -2 | 2 | -2 | -2 | -3 |
| 5 | 4 | 1 | 1 | 0 | 0 | 0 | 0 | -1 | -1 | -1 | -1 | -2 | 2 | -2 | -2 | -3 |
| 6 | 5 | 2 | 2 | 0 | 0 | 0 | 0 | -1 | -1 | -1 | -1 | -2 | 2 | -2 | -2 | -3 |
| 7 | 6 | 2 | 2 | 0 | 0 | 0 | 0 | -1 | -1 | -1 | -1 | -2 | 2 | -2 | -2 | -3 |
| 8 | 7 | 3 | 3 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 |
| 9 | 8 | 3 | 3 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 |
| 10 | 9 | 4 | 4 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 |
| 11 | 10 | 4 | 4 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 |
| 12 | 11 | 5 | 5 | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 |
| 13 | 12 | 5 | 5 | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 |
| 14 | 13 | 6 | 6 | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 |
| 15 | 14 | 6 | 6 | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 |
| 16 | 15 | 7 | 7 | 3 | 3 | 3 | 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |

1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define LL long long 4 using namespace std; 5 bool infer(LL x) 6 { 7 int s=0; 8 while(x) 9 { 10 if(x&1) 11 { 12 s++; 13 } 14 x>>=1; 15 } 16 if(s&1) 17 return 1; 18 else 19 return 0; 20 } 21 map<LL,bool> num; 22 int main() 23 { 24 int n,T,k,l; 25 LL sum,m; 26 while(scanf("%d",&n)!=EOF) 27 { 28 num.erase(num.begin(),num.end()); 29 sum=0; 30 for(int i=1;i<=n;i++) 31 { 32 scanf("%lld",&m); 33 if(num[m]==1) 34 continue; 35 num[m]=1; 36 if(infer(m)) 37 sum^=2*m; 38 else 39 sum^=2*m+1; 40 } 41 if(sum==0) 42 printf("Yes "); 43 else 44 printf("No "); 45 } 46 return 0; 47 }
18.hdu 3863
No Gambling
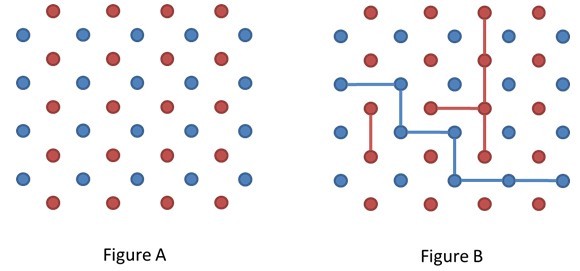
In the game, the two players take turns to choose two points to get connected by a stick. The two chosen points’ distance should be exactly one-unit length. The first player’s goal is to create a ‘bridge’ that connects a most left point and a most right point. The second player’s goal is to create a ‘bridge’ that connects a most top point and a most bottom point. Figure B shows a possible result (the first player won). In addition, the stick shouldn’t get crossed.
Now Flyvan will give the number N, and his two friends will play the game. Both of the two players will choose the best strategy. You can bet on one player, and if he wins the game, you’ll get twice money you bet~
Since you are a talented programmer, you surely won’t just do gambling. Please write a program to find out the player who you should bet on. As Oregon Maple is elder, he will always play first.

1 #include<bits/stdc++.h> 2 #define LL long long 3 using namespace std; 4 int main() 5 { 6 LL n; 7 while(scanf("%lld",&n)!=EOF && n!=-1) 8 { 9 printf("I bet on Oregon Maple~ "); 10 } 11 return 0; 12 }
19.hdu 3951
Coin Game

The game goes like this:
Two players start the game with a circle of n coins.
They take coins from the circle in turn and every time they could take 1~K continuous coins.
(imagining that ten coins numbered from 1 to 10 and K equal to 3, since 1 and 10 are continuous, you could take away the continuous 10 , 1 , 2 , but if 2 was taken away, you couldn't take 1, 3, 4, because 1 and 3 aren't continuous)
The player who takes the last coin wins the game.
Suppose that those two players always take the best moves and never make mistakes.
Your job is to find out who will definitely win the game.
Each case contains two integers N(3<=N<=109,1<=K<=10).
$k=1$时判奇偶决定输赢。

1 #include<bits/stdc++.h> 2 #define LL long long 3 using namespace std; 4 int main() 5 { 6 LL n,k,T,kase=0; 7 scanf("%d",&T); 8 while(T--) 9 { 10 scanf("%lld%lld",&n,&k); 11 if(k==1) 12 { 13 if(n%2==0) 14 printf("Case %d: second ",++kase); 15 else 16 printf("Case %d: first ",++kase); 17 } 18 else if(k>=n) 19 printf("Case %d: first ",++kase); 20 else 21 printf("Case %d: second ",++kase); 22 } 23 return 0; 24 }
20.hdu 2188
悼念512汶川大地震遇难同胞——选拔志愿者
选拔规则如下:
1、最初的捐款箱是空的;
2、两人轮流捐款,每次捐款额必须为正整数,并且每人每次捐款最多不超过m元(1<=m<=10)。
3、最先使得总捐款额达到或者超过n元(0<n<10000)的一方为胜者,则其可以亲赴灾区服务。
我们知道,两人都很想入选志愿者名单,并且都是非常聪明的人,假设林队先捐,请你判断谁能入选最后的名单?
bash博弈

1 #include<cstdio> 2 #include<iostream> 3 using namespace std; 4 int main() 5 { 6 int n,m,k,l; 7 scanf("%d",&k); 8 for(int i=0;i<k;i++) 9 { 10 scanf("%d%d2",&n,&m); 11 if(n%(m+1)==0) 12 printf("Rabbit "); 13 else 14 printf("Grass "); 15 } 16 return 0; 17 18 }
21.hdu 2149
Public Sale
要种田得有田才行,Lele听说街上正在举行一场别开生面的拍卖会,拍卖的物品正好就是一块20亩的田地。于是,Lele带上他的全部积蓄,冲往拍卖会。
后来发现,整个拍卖会只有Lele和他的死对头Yueyue。
通过打听,Lele知道这场拍卖的规则是这样的:刚开始底价为0,两个人轮流开始加价,不过每次加价的幅度要在1~N之间,当价格大于或等于田地的成本价 M 时,主办方就把这块田地卖给这次叫价的人。
Lele和Yueyue虽然考试不行,但是对拍卖却十分精通,而且他们两个人都十分想得到这块田地。所以他们每次都是选对自己最有利的方式进行加价。
由于Lele字典序比Yueyue靠前,所以每次都是由Lele先开始加价,请问,第一次加价的时候,
Lele要出多少才能保证自己买得到这块地呢?
每组测试包含两个整数M和N(含义见题目描述,0<N,M<1100)
如果Lele在第一次无论如何出价都无法买到这块土地,就输出"none"。

1 #include<bits/stdc++.h> 2 #define LL long long 3 using namespace std; 4 int main() 5 { 6 int n,m; 7 while(scanf("%d%d",&n,&m)!=EOF) 8 { 9 if(m>=n) 10 { 11 for(int i=n;i<m;i++) 12 { 13 printf("%d ",i); 14 } 15 printf("%d ",m); 16 continue; 17 } 18 if(n%(m+1)==0) 19 { 20 printf("none "); 21 continue; 22 } 23 printf("%d ",n%(m+1)); 24 } 25 return 0; 26 }
22
