插头dp练习

最近学了插头dp，准备陆续更新插头dp类练习。

学习论文还是cdq那篇《基于连通性状态压缩的动态规划问题》。

基本的想法都讲得很通透了，接下来就靠自己yy了。

还有感谢kuangbin大大的专题练习。

首先入门肯定写个n*m*state的插头dp，没为什么，这东西好写啊~

然后你就想着，当n*m特别大的时候我该怎么解决呢（m不可能特别大，因为他决定了状态数state）。

你会发现这个dp只针对前一种状态和后一种状态进行转移。

所以你能最后把他压缩成2*state的插头dp，当然这么写肯定是很麻烦的写法，但是极为节省空间。

首先是基础题：

hdu 1693

Eat the Trees

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4168    Accepted Submission(s): 2091

Problem Description

Most of us know that in the game called DotA(Defense of the Ancient), Pudge is a strong hero in the first period of the game. When the game goes to end however, Pudge is not a strong hero any more.
So Pudge’s teammates give him a new assignment—Eat the Trees!

The trees are in a rectangle N * M cells in size and each of the cells either has exactly one tree or has nothing at all. And what Pudge needs to do is to eat all trees that are in the cells.
There are several rules Pudge must follow:
I. Pudge must eat the trees by choosing a circuit and he then will eat all trees that are in the chosen circuit.
II. The cell that does not contain a tree is unreachable, e.g. each of the cells that is through the circuit which Pudge chooses must contain a tree and when the circuit is chosen, the trees which are in the cells on the circuit will disappear.
III. Pudge may choose one or more circuits to eat the trees.

Now Pudge has a question, how many ways are there to eat the trees?
At the picture below three samples are given for N = 6 and M = 3(gray square means no trees in the cell, and the bold black line means the chosen circuit(s))

 

Input

The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 10 cases.
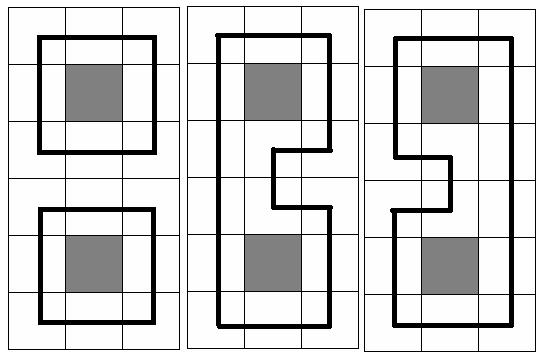
For each case, the first line contains the integer numbers N and M, 1<=N, M<=11. Each of the next N lines contains M numbers (either 0 or 1) separated by a space. Number 0 means a cell which has no trees and number 1 means a cell that has exactly one tree.

 

Output

For each case, you should print the desired number of ways in one line. It is guaranteed, that it does not exceed 2⁶³ – 1. Use the format in the sample.

 

Sample Input

2 6 3 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 2 4 1 1 1 1 1 1 1 1

 

Sample Output

Case 1: There are 3 ways to eat the trees. Case 2: There are 2 ways to eat the trees.

---

基础题嘛，很容易想到转移方程。鉴于我嫌麻烦，写了空间复杂度较高的代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#define clr(x) memset(x,0,sizeof(x))
#define LL long long
using namespace std;
LL dp[20][20][1<<12+1];
int mp[100][100];
int main()
{
    int T,n,m,k,t1,t2,kase=0;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                scanf("%d",&mp[i][j]);
        clr(dp);
        dp[0][m][0]=1;
        for(int i=1;i<=n;i++)
        {
            for(int k=0;k<(1<<m);k++)
            {
                dp[i][0][k<<1]=dp[i-1][m][k];
            }
            for(int j=1;j<=m;j++)
            {
                for(int k=0;k<(1<<(m+1));k++)
                {
                    t2=1<<j;
                    t1=1<<(j-1);
                    if(mp[i][j])
                    {
                        if(((k&t2)==0 && (k&t1)!=0) || ((k&t2)!=0 && (k&t1)==0))
                            dp[i][j][k]+=dp[i][j-1][k];
                        dp[i][j][k]+=dp[i][j-1][k^t1^t2];
                    }
                    else
                    {
                       if((k&t1)==0&&(k&t2)==0)dp[i][j][k]+=dp[i][j-1][k];
                    }
                }
            }
        }
        printf("Case %d: There are %lld ways to eat the trees.
",++kase,dp[n][m][0]);
    }
    return 0;
}

fzu 1977

Pandora adventure

Problem Description

The pollution of the earth is so serious that people can not survive any more. Fortunately, people have found a new planet that maybe has life, and we call it "Pandora Planet".

Leonardo Da Vinci is the only astronaut on the earth. He will be sent to the Pandora Planet to gather some plant specimens and go back. The plant specimen is important to the people to decide whether the planet is fit to live or not.

Assuming that Da Vinci can only move in an N×M grid. The positions of the plant specimens he wants to collect are all marked by the satellite. His task is to find a path to collect all the plant specimens and return to the spaceship. There are some savage beasts in the planet. Da Vinci can not investigate the grid with the savage beast. These grids are also marked by the satellite. In order to save time Da Vinci could only visit each grid exactly once and also return to the start grid, that is, you can not visit a grid twice except the start grid. You should note that you can choose any grid as the start grid.

Now he wants to know the number of different paths he can collect all the plant specimens. We only care about the path and ignore where the start grid is, so the two paths in Figure 1 are considered as the same.

Figure 1

Input

The first line of the input contains an integer T (T≤100), indicating the number of cases. Each case begins with a line containing two integers N and M (1≤N, M≤12), the size of the planet is N×M. Each of the following N lines contains M characters Gij(1≤i≤N, 1≤j≤M), G_ij denotes the status of the grid in row i and column j, where 'X' denotes the grid with savage beast, '*' denotes the safe grid that you can decide to go or not, 'O' denotes the plant specimen you should collect. We guarantee that there are at least three plant specimens in the map.

Output

For each test case, print a line containing the test case number (beginning with 1) and the number of different paths he can collect all the plant specimens. You can make sure that the answer will fit in a 64-bit signed integer.

Sample Input

2 2 2 OO O* 4 4 ***O XO** **O* XX**

Sample Output

Case 1: 1 Case 2: 7 

---

三种格子：必经过，不能经过，经不经过无所谓。然后求只有一条的欧拉回路。

在kuangbin模板上改进，使用括号序列求解。

我们增加一个标记位来标记是否形成回路。

若该状态形成回路且各位状态不全为0，则不转移。

若该状态形成回路各位状态都为0，但后续的点有必过点，则该状态不转移。

必经过和经不经过无所谓点转移相似，后者多一个上插头和左插头皆为0下的转移状态。

不能经过点的所有状态都转移至下一状态，该点插头不变（都为0）。

#include<cstdio>
#include<iostream>
#include<cstring>
#define clr(x) memset(x,0,sizeof(x))
#define clr_1(x) memset(x,-1,sizeof(x))
#define LL long long 
#define HASH 10007
#define STATE 1000010
using namespace std;
struct hashmap
{
    int size;
    int next[STATE],state[STATE],head[HASH];
    LL fas[STATE];
    void init()
    {
        size=0;
        clr_1(head);
    }
    void add(int st,LL solu)
    {
        int k=st%HASH;
        for(int i=head[k];i!=-1;i=next[i])
            if(st==state[i])
            {
                fas[i]+=solu;
                return;
            }
        next[++size]=head[k];
        fas[size]=solu;
        state[size]=st;
        head[k]=size;
        return ;
    }
}dp[2];
int maped[20][20],endflag;
char s[20];
int code[20];
void init(int n,int m)
{
    clr(maped);
    for(int i=1;i<=n;i++)
    {
        scanf("%s",s);
        for(int j=0;j<m;j++)
        {
            if(s[j]=='*')
              maped[i][j+1]=1;
            if(s[j]=='O')
              maped[i][j+1]=2;
        }
    }
    return ;
}
void decode(int st,int *code,int m)
{
    endflag=st&1;
    st>>=1;
    for(int i=m;i>=0;i--)
    {
        code[i]=st&3;
        st>>=2;
    }
    return ;
}
int encode(int *code,int m)
{
    int st=0;
    for(int i=0;i<=m;i++)
    {
        st<<=2;
        st|=code[i];
    }
    st<<=1;
    st|=endflag;
    return st;
}
void shift(int *code,int m)
{
    for(int i=m;i>0;i--)
        code[i]=code[i-1];
    code[0]=0;
    return ;
}
void dpblank(int i,int j,int cnt,int m)
{
    int top,left,up;
    for(int it=1;it<=dp[cnt].size;it++)
    {
        decode(dp[cnt].state[it],code,m);
        left=code[j-1];
        up=code[j];
        if(endflag &&((dp[cnt].state[it]>>1)>0 || maped[i][j]==2)) continue;
        if(left && up)
        {
            if(left!=up)
            {
                code[j]=code[j-1]=0;
                if(left==1) endflag=1;
                if(j==m) shift(code,m); 
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]);
            }
            else
            {
                if(left==2)
                {
                    top=0;
                    for(int k=j-2;k>=0;k--)
                    {
                        if(code[k]==2)
                            top++;
                        if(code[k]==1)
                            if(top>0)
                                top--;
                            else
                                {
                                    code[k]=2;
                                    break;
                                }
                    }
                }
                else
                {
                    top=0;
                    for(int k=j+1;k<=m;k++)
                    {
                        if(code[k]==1)
                            top++;
                        if(code[k]==2)
                            if(top>0)
                                top--;
                            else
                                {
                                    code[k]=1;
                                    break;
                                }
                    }                
                }
                code[j]=code[j-1]=0;
                if(j==m) shift(code,m);
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]);
            }
        }
        else if(left || up)
        {
            if(left) top=left;
            else top=up;
            if(maped[i][j+1])
            {
                code[j-1]=0;
                code[j]=top;
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]);                
            }
            if(maped[i+1][j])
            {
                code[j-1]=top;
                code[j]=0;
                if(j==m) shift(code,m);
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]);                
            }
        }
        else
        {
            if(maped[i][j+1] && maped[i+1][j])
            {
                code[j-1]=1;
                code[j]=2;
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]);    
            }
            if(maped[i][j]==1)
            {
                code[j-1]=code[j]=0;
                if(j==m) shift(code,m);
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]);                        
            }        
        }        
    }
    return ;
}
void dpnone(int i,int j,int cnt,int m)
{
    for(int it=1;it<=dp[cnt].size;it++)
    {
        decode(dp[cnt].state[it],code,m);
        if(endflag &&((dp[cnt].state[it]>>1)>0 || maped[i][j]==2)) continue;
        code[j]=code[j-1]=0;
        if(j==m) shift(code,m);
        dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]);        
    }
    return ;
}
LL solve(int n,int m)
{
    int cnt=0;
    LL ans=0;
    dp[cnt].init();
    dp[cnt].add(0,1);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            dp[cnt^1].init();
            if(maped[i][j]==0)
                dpnone(i,j,cnt,m);
            else
                dpblank(i,j,cnt,m);
            cnt^=1;
/*            for(int it=1;it<=dp[cnt].size;it++)
            {
                decode(dp[cnt].state[it],code,m);
                for(int k=0;k<=m;k++)
                    printf("%d:%d ",k,code[k]);
                printf("FLAG:%d fas:%lld
",endflag,dp[cnt].fas[it]);
            }
            printf("
"); */
        }
    }
    for(int i=1;i<=dp[cnt].size;i++)
        ans+=dp[cnt].fas[i];
    return ans;
}
int main()
{
    int T,n,m;
    scanf("%d",&T);
    for(int kase=1;kase<=T;kase++)
    {
        scanf("%d%d",&n,&m);
        init(n,m);
        printf("Case %d: %lld
",kase,solve(n,m));
    }
    return 0;
}

hdu 1964

Pipes

Time Limit: 5000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 917    Accepted Submission(s): 448

Problem Description

The construction of office buildings has become a very standardized task. Pre-fabricated modules are combined according to the customer’s needs, shipped from a faraway factory, and assembled on the construction site. However, there are still some tasks that require careful planning, one example being the routing of pipes for the heating system. 

Amodern office building ismade up of squaremodules, one on each floor being a service module from which (among other things) hot water is pumped out to the other modules through the heating pipes. Each module (including the service module) will have heating pipes connecting it to exactly two of its two to four neighboring modules. Thus, the pipes have to run in a circuit, from the service module, visiting each module exactly once, before finally returning to the service module. Due to different properties of the modules, having pipes connecting a pair of adjacent modules comes at different costs. For example, some modules are separated by thick walls, increasing the cost of laying pipes. Your task is to, given a description of a floor of an office building, decide the cheapest way to route the heating pipes.

 

Input

The first line of input contains a single integer, stating the number of floors to handle. Then follow n floor descriptions, each beginning on a new line with two integers, 2 <= r <= 10 and 2 <= c <= 10, defining the size of the floor – r-by-c modules. Beginning on the next line follows a floor description in ASCII format, in total 2r + 1 rows, each with 2c + 2 characters, including the final newline. All floors are perfectly rectangular, and will always have an even number of modules. All interior walls are represented by numeric characters, ’0’ to ’9’, indicating the cost of routing pipes through the wall (see sample input).

 

Output

For each test case, output a single line with the cost of the cheapest route.

 

Sample Input

3 4 3 ####### # 2 3 # #1#9#1# # 2 3 # #1#7#1# # 5 3 # #1#9#1# # 2 3 # ####### 4 4 ######### # 2 3 3 # #1#9#1#4# # 2 3 6 # #1#7#1#5# # 5 3 1 # #1#9#1#7# # 2 3 0 # ######### 2 2 ##### # 1 # #2#3# # 4 # #####

 

Sample Output

28 45 10

 

---

插头dp模板题，把方案数改成最小数量然后做点小修改就好了。拿上一题的模板做做就行。

#include<cstdio>
#include<iostream>
#include<cstring>
#define clr(x) memset(x,0,sizeof(x))
#define clr_1(x) memset(x,-1,sizeof(x))
#define LL long long 
#define HASH 10007
#define STATE 1000010
using namespace std;
struct hashmap
{
    int size;
    int next[STATE],head[HASH];
    LL state[STATE];
    LL fas[STATE];
    void init()
    {
        size=0;
        clr_1(head);
    }
    void add(LL st,LL solu)
    {
        int k=st%HASH;
        for(int i=head[k];i!=-1;i=next[i])
            if(st==state[i])
            {
                if(fas[i]>solu)
                    fas[i]=solu;
                return;
            }
        next[++size]=head[k];
        fas[size]=solu;
        state[size]=st;
        head[k]=size;
        return ;
    }
}dp[2];
int maped[40][40],endflag;
char s[40];
int code[40];
void init(int n,int m)
{
    clr(maped);
    fgets(s,100,stdin);
    for(int i=1;i<=n;i++)
    {
        fgets(s,100,stdin);
        for(int j=0;j<m;j++)
        {
            if(s[j]==' ')
              maped[i][j+1]=11;
            if(s[j]>='0' && s[j]<='9')
              maped[i][j+1]=s[j]-'0'+1;
        }
    }
    return ;
}
void decode(LL st,int *code,int m)
{
    endflag=st&1;
    st>>=1;
    for(int i=m;i>=0;i--)
    {
        code[i]=st&3;
        st>>=2;
    }
    return ;
}
LL encode(int *code,int m)
{
    LL st=0;
    for(int i=0;i<=m;i++)
    {
        st<<=2;
        st|=code[i];
    }
    st<<=1;
    st|=endflag;
    return st;
}
void shift(int *code,int m)
{
    for(int i=m;i>0;i--)
        code[i]=code[i-1];
    code[0]=0;
    return ;
}
void dpblank(int i,int j,int cnt,int m)
{
    int top,left,up;
    LL cost;
    if(maped[i][j]==11)
        cost=0;
    else
        cost=1LL*(maped[i][j]-1);
    for(int it=1;it<=dp[cnt].size;it++)
    {
        decode(dp[cnt].state[it],code,m);
        if(endflag &&((dp[cnt].state[it]>>1)>0 || maped[i][j]==2)) continue;
        left=code[j-1];
        up=code[j];
        if(left && up)
        {
            if(left!=up)
            {
                code[j]=code[j-1]=0;
                if(left==1) endflag=1;
                if(j==m) shift(code,m); 
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);
            }
            else
            {
                if(left==2)
                {
                    top=0;
                    for(int k=j-2;k>=0;k--)
                    {
                        if(code[k]==2)
                            top++;
                        if(code[k]==1)
                            if(top>0)
                                top--;
                            else
                                {
                                    code[k]=2;
                                    break;
                                }
                    }
                }
                else
                {
                    top=0;
                    for(int k=j+1;k<=m;k++)
                    {
                        if(code[k]==1)
                            top++;
                        if(code[k]==2)
                            if(top>0)
                                top--;
                            else
                                {
                                    code[k]=1;
                                    break;
                                }
                    }                
                }
                code[j]=code[j-1]=0;
                if(j==m) shift(code,m);
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);
            }
        }
        else if(left || up)
        {
            if(left) top=left;
            else top=up;
            if(maped[i][j+1])
            {
                code[j-1]=0;
                code[j]=top;
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);                
            }
            if(maped[i+1][j])
            {
                code[j-1]=top;
                code[j]=0;
                if(j==m) shift(code,m);
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);                
            }
        }
        else
        {
            if(maped[i][j+1] && maped[i+1][j])
            {
                code[j-1]=1;
                code[j]=2;
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);    
            }
            if(maped[i][j]!=11)
            {
                code[j-1]=code[j]=0;
                if(j==m) shift(code,m);
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]);                        
            }        
        }        
    }
    return ;
}
void dpnone(int i,int j,int cnt,int m)
{
    for(int it=1;it<=dp[cnt].size;it++)
    {
        decode(dp[cnt].state[it],code,m);
        if(endflag &&((dp[cnt].state[it]>>1)>0 || maped[i][j]==2)) continue;
        if(j==m) shift(code,m);
        dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]);
    }
    return ;
}
LL solve(int n,int m)
{
    int cnt=0;
    LL ans=0;
    dp[cnt].init();
    dp[cnt].add(0,0);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            dp[cnt^1].init();
            if(maped[i][j]==0)
                dpnone(i,j,cnt,m);
            else
                dpblank(i,j,cnt,m);
            cnt^=1;
/*            for(int it=1;it<=dp[cnt].size;it++)
            {
                decode(dp[cnt].state[it],code,m);
                for(int k=0;k<=m;k++)
                    printf("%d:%d ",k,code[k]);
                printf("FLAG:%d fas:%lld
",endflag,dp[cnt].fas[it]);
            }
            printf("
"); */
        }
    }
    for(int i=1;i<=dp[cnt].size;i++)
        ans+=dp[cnt].fas[i];
    return ans;
}
int main()
{
    int T,n,m;
    scanf("%d",&T);
    for(int kase=1;kase<=T;kase++)
    {
        scanf("%d%d",&n,&m);
        n=2*n+1;
        m=2*m+1;
        init(n,m);
        printf("%lld
",solve(n,m));
    }
    return 0;
}

 hdu 3377

Plan

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1436    Accepted Submission(s): 517

Problem Description

One day, Resty comes to an incredible world to seek Eve -- The origin of life. Lilith, the sister of Eve, comes with him. Although Resty wants to find Eve as soon as possible, Lilith likes to play games so much that you can't make her make any move if you don't play with her.

Now they comes to the magical world and Lilish ask Resty to play with her.

The game is following :
Now the world is divided into a m * n grids by Lilith, and Lilith gives each grid a score.
So we can use a matrix to describe it.
You should come from cell(0, 0) to cell(m-1, n-1) (Up-Left to Down-Right) and try to colloct as more score as possible.
According to Lilish's rule, you can't arrive at each cell more than once.

Resty knows that Lilish will be easy to find the max score, and he doesn't want to lose the game.
So he want to find the game plan to reach the max score.

Your task is to calculate the max score that Lilish will find, the map is so small so it shouldn't be difficult for you, right?

 

Input

The input consists of more than one testdata.
Process to the END OF DATA.
For each test data :
the first live give m and n. (1<=m<=8, 1<=n<=9)
following m lines, each contain n number to give you the m*n matrix.
each number in the matrix is between -2000 and 2000

 

Output

Output Format is "Case ID: ANS" one line for each data
Don't print any empty line to the output

 

Sample Input

2 2 1 2 3 1 3 3 0 -20 100 1 -20 -20 1 1 1

 

Sample Output

Case 1: 5 Case 2: 61

---

这题仍然可以用回路做，value数组存经过的贡献，maped存是否可走（可走，不可走，必过)。

你在原图周围填上两圈，最外圈和原图里都是可走区域，次外圈除了两个格子全为不可走区域（两个格子是和(0,0)相邻任意一个格子及（n-1，m-1)相邻的任意一个格子）。特别的原来的(0,0)（n-1，m-1)这两个格子以及最外圈的任意一个格子设置为必过格子，然后用上一题的类似的回路模板可做。

样子类似于：

1 1 1 1 1 1 1 2

1 0 1 0 0 0 0 1

1 0 2 1 1 1 0 1

1 0 1 1 1 2 0 1

1 0 0 0 0 1 0 1

1 1 1 1 1 1 1 1

这样的一个矩阵。

然后代码（405ms）：

#include<cstdio>
#include<iostream>
#include<cstring>
#define clr(x) memset(x,0,sizeof(x))
#define clr_1(x) memset(x,-1,sizeof(x))
#define LL long long 
#define HASH 10007
#define STATE 1000010
using namespace std;
struct hashmap
{
    int size;
    int next[STATE],head[HASH];
    LL state[STATE];
    LL fas[STATE];
    void init()
    {
        size=0;
        clr_1(head);
    }
    void add(LL st,LL solu)
    {
        int k=st%HASH;
        for(int i=head[k];i!=-1;i=next[i])
            if(st==state[i])
            {
                if(fas[i]<solu)
                    fas[i]=solu;
                return;
            }
        next[++size]=head[k];
        fas[size]=solu;
        state[size]=st;
        head[k]=size;
        return ;
    }
}dp[2];
int maped[40][40],value[40][40],endflag;
char s[40];
int code[40];
void init(int &n,int &m)
{
    clr(maped);
    clr(value);
    for(int i=2;i<=n+1;i++)
    {
        for(int j=2;j<=m+1;j++)
        {
            maped[i][j]=1;
            scanf("%d",&value[i][j]);
        }
    }
    n+=3;
    m+=3;
    for(int i=0;i<=n;i++)
        maped[i][0]=maped[i][m]=1;
    for(int i=0;i<=m;i++)
        maped[0][i]=maped[n][i]=1;
    maped[1][2]=1;
    maped[n-1][m-2]=1;
    maped[2][2]=maped[n-2][m-2]=2;    
    maped[n][m]=2;
/*    for(int i=0;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
            printf("%d ",maped[i][j]);
        printf("
");
    }*/
    return ;
}
void decode(LL st,int *code,int m)
{
    endflag=st&1;
    st>>=1;
    for(int i=m;i>=0;i--)
    {
        code[i]=st&3;
        st>>=2;
    }
    return ;
}
LL encode(int *code,int m)
{
    LL st=0;
    for(int i=0;i<=m;i++)
    {
        st<<=2;
        st|=code[i];
    }
    st<<=1;
    st|=endflag;
    return st;
}
void shift(int *code,int m)
{
    for(int i=m;i>0;i--)
        code[i]=code[i-1];
    code[0]=0;
    return ;
}
void dpblank(int i,int j,int cnt,int m)
{
    int top,left,up;
    LL cost=1LL*value[i][j];
    for(int it=1;it<=dp[cnt].size;it++)
    {
        decode(dp[cnt].state[it],code,m);
        if(endflag &&((dp[cnt].state[it]>>1)>0 || maped[i][j]==2)) continue;
        left=code[j-1];
        up=code[j];
        if(left && up)
        {
            if(left!=up)
            {
                code[j]=code[j-1]=0;
                if(left==1) endflag=1;
                if(j==m) shift(code,m); 
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);
            }
            else
            {
                if(left==2)
                {
                    top=0;
                    for(int k=j-2;k>=0;k--)
                    {
                        if(code[k]==2)
                            top++;
                        if(code[k]==1)
                            if(top>0)
                                top--;
                            else
                                {
                                    code[k]=2;
                                    break;
                                }
                    }
                }
                else
                {
                    top=0;
                    for(int k=j+1;k<=m;k++)
                    {
                        if(code[k]==1)
                            top++;
                        if(code[k]==2)
                            if(top>0)
                                top--;
                            else
                                {
                                    code[k]=1;
                                    break;
                                }
                    }                
                }
                code[j]=code[j-1]=0;
                if(j==m) shift(code,m);
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);
            }
        }
        else if(left || up)
        {
            if(left) top=left;
            else top=up;
            if(maped[i][j+1])
            {
                code[j-1]=0;
                code[j]=top;
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);                
            }
            if(maped[i+1][j])
            {
                code[j-1]=top;
                code[j]=0;
                if(j==m) shift(code,m);
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);                
            }
        }
        else
        {
            if(maped[i][j+1] && maped[i+1][j])
            {
                code[j-1]=1;
                code[j]=2;
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);    
            }
            if(maped[i][j]==1)
            {
                code[j-1]=code[j]=0;
                if(j==m) shift(code,m);
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]);                        
            }        
        }        
    }
    return ;
}
void dpnone(int i,int j,int cnt,int m)
{
    for(int it=1;it<=dp[cnt].size;it++)
    {
        decode(dp[cnt].state[it],code,m);
        if(endflag &&((dp[cnt].state[it]>>1)>0 || maped[i][j]==2)) continue;
        if(j==m) shift(code,m);
        dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]);
    }
    return ;
}
LL solve(int n,int m)
{
    int cnt=0;
    LL ans=0;
    dp[cnt].init();
    dp[cnt].add(0,0);
    for(int i=0;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            dp[cnt^1].init();
            if(maped[i][j]==0)
                dpnone(i,j,cnt,m);
            else
                dpblank(i,j,cnt,m);
            cnt^=1;
/*            for(int it=1;it<=dp[cnt].size;it++)
            {
                decode(dp[cnt].state[it],code,m);
                for(int k=0;k<=m;k++)
                    printf("%d:%d ",k,code[k]);
                printf("FLAG:%d fas:%lld
",endflag,dp[cnt].fas[it]);
            }
            printf("
"); */
        }
    }
    for(int i=1;i<=dp[cnt].size;i++)
        ans+=dp[cnt].fas[i];
    return ans;
}
int main()
{
    int n,m,kase=0;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        init(n,m);
        printf("Case %d: %lld
",++kase,solve(n,m));
    }
    return 0;
}

然后我之前是用独立插头做的，终于过了（78ms）：

#include<cstdio>
#include<iostream>
#include<cstring>
#define clr(x) memset(x,0,sizeof(x))
#define clr_1(x) memset(x,-1,sizeof(x))
#define LL long long 
#define HASH 10007
#define STATE 1000010
using namespace std;
struct hashmap//hash表存状态及大的数和 
{
    int size;
    int next[STATE],head[HASH];
    LL state[STATE];
    LL fas[STATE];
    void init()//清空 
    {
        size=0;
        clr_1(head);
    }
    void add(LL st,LL solu)//状态加入，若已有该状态则取较大者 
    {
        int k=st%HASH;
        for(int i=head[k];i!=-1;i=next[i])
            if(st==state[i])
            {
                if(fas[i]<solu)
                    fas[i]=solu;
                return;
            }
        next[++size]=head[k];
        fas[size]=solu;
        state[size]=st;
        head[k]=size;
        return ;
    }
}dp[2];
int maped[40][40];
int code[40];
void init(int n,int m)//初始化值，读入maped 
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&maped[i][j]);
        }
    }
    return ;
}
void decode(LL st,int *code,int m)//解码，括号序列 
{
    for(int i=m;i>=0;i--)
    {
        code[i]=st&3;
        st>>=2;
    }
    return ;
}
LL encode(int *code,int m)//编码，括号序列 
{
    LL st=0;
    for(int i=0;i<=m;i++)
    {
        st<<=2;
        st|=code[i];
    }
    return st;
}
void shift(int *code,int m)//左移操作 
{
    for(int i=m;i>0;i--)
        code[i]=code[i-1];
    code[0]=0;
    return ;
}
void dpblank(int i,int j,int cnt,int n,int m)//空格子状态转移 
{
    int top,left,up;
    LL cost;
    cost=1LL*maped[i][j];
    if(i==1 &&j==1)//i=1 且 j=1时加入只有下独立插头 和 右独立插头的状态 
    {
        decode(dp[cnt].state[1],code,m);
        if(j+1<=m)
        {
            code[j-1]=0;
            code[j]=3;
            dp[cnt^1].add(encode(code,m),dp[cnt].fas[1]+cost);    
        }    
        if(i+1<=n)
        {
            code[j-1]=3;
            code[j]=0;
            if(j==m) shift(code,m);
            dp[cnt^1].add(encode(code,m),dp[cnt].fas[1]+cost);                
        }
        return ;
    }
    if(i==n &&j==m)//i=n 且 j=m时截止单个独立插头的状态 
    {
        for(int it=1;it<=dp[cnt].size;it++)
        {
            decode(dp[cnt].state[it],code,m);
            code[j-1]=code[j]=0;
            if(j==m) shift(code,m);
            dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);            
        }
        return ;
    }
    for(int it=1;it<=dp[cnt].size;it++)
    {
        decode(dp[cnt].state[it],code,m);
        left=code[j-1];
        up=code[j];
        if(left && up)//上插头和左插头都存在 
        {
            if(left==3 || up==3)//存在一个独立插头
            {
                if(up==2|| left==2)//若另一个插头为右括号插头，则找到对应的左括号插头变为独立插头 
                {
                    top=0;
                    for(int k=j-2;k>=0;k--)
                    {
                        if(code[k]==2)
                            top++;
                        if(code[k]==1)
                            if(top>0)
                                top--;
                            else
                                {
                                    code[k]=3;
                                    break;
                                }
                    }                        
                }
                else if(up==1 ||left==1)//若另一个插头为左括号插头，则找到对应的右括号插头变为独立插头 
                {
                    top=0;
                    for(int k=j+1;k<=m;k++)
                    {
                        if(code[k]==1)
                            top++;
                        if(code[k]==2)
                            if(top>0)
                                top--;
                            else
                                {
                                    code[k]=3;
                                    break;
                                }
                    }                                    
                }
                code[j]=code[j-1]=0;
                if(j==m) shift(code,m);
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);
            }
            else if(left!=up)//两个括号插头 
            {
                if(left==1)//左右括号插头，不允许形成回路 
                    continue;
                else//右左括号插头直接去掉 
                {
                    code[j]=code[j-1]=0;
                    if(j==m) shift(code,m);
                    dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);                    
                 } 
            }
            else
            {
                if(left==2)//都是左括号插头，找到对应的第一个右括号插头变为左括号插头 
                {
                    top=0;
                    for(int k=j-2;k>=0;k--)
                    {
                        if(code[k]==2)
                            top++;
                        if(code[k]==1)
                            if(top>0)
                                top--;
                            else
                                {
                                    code[k]=2;
                                    break;
                                }
                    }
                }
                else//都是右括号插头，找到对应的第一个左括号插头变为右括号插头  
                {
                    top=0;
                    for(int k=j+1;k<=m;k++)
                    {
                        if(code[k]==1)
                            top++;
                        if(code[k]==2)
                            if(top>0)
                                top--;
                            else
                                {
                                    code[k]=1;
                                    break;
                                }
                    }                
                }
                code[j]=code[j-1]=0;
                if(j==m) shift(code,m);
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);
            }
        }
        else if(left || up)//仅有一个插头，则延伸插头 
        {
            if(left) top=left;
            else top=up;
            if(j+1<=m)//右延伸插头 
            {
                code[j-1]=0;
                code[j]=top;
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);                
            }
            if(i+1<=n)//下延伸插头 
            {
                code[j-1]=top;
                code[j]=0;
                if(j==m) shift(code,m);
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);                
            }
        }
        else//没有插头 
        {
            if(j+1<=m && i+1<=n)//下插头和左插头 
            {
                code[j-1]=1;
                code[j]=2;
                dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]+cost);    
            }
            //可经过可不经过点则可以保持原样，没有插头 
            code[j-1]=code[j]=0;
            if(j==m) shift(code,m);
            dp[cnt^1].add(encode(code,m),dp[cnt].fas[it]);                            
        }        
    }
    return ;
}
LL solve(int n,int m)
{
    int cnt=0;
    LL ans=0;
    if(n==1 && m==1)
        return ans=1LL*maped[1][1];
    dp[cnt].init();
    dp[cnt].add(0,0);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            dp[cnt^1].init();
            dpblank(i,j,cnt,n,m);
            cnt^=1;
/*            for(int it=1;it<=dp[cnt].size;it++)
            {
                decode(dp[cnt].state[it],code,m);
                for(int k=0;k<=m;k++)
                    printf("%d:%d ",k,code[k]);
                printf("fas:%lld
",dp[cnt].fas[it]);
            }
            printf("
"); */
        }
    }
    for(int i=1;i<=dp[cnt].size;i++)
        ans+=dp[cnt].fas[i];
    return ans;
}
int main()
{
    int n,m,kase=0;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        init(n,m);
        printf("Case %d: %lld
",++kase,solve(n,m));
    }
    return 0;
}

可见增加一维可能导致时间暴增，所以能少递推次数尽量少。

 还有测过kuangbin的代码，178ms。状态数过多吧容易变慢。

hdu 3633

Black and white

Time Limit: 20000/10000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 254    Accepted Submission(s): 76
Special Judge

Problem Description

Given a partially filled grid with N rows and M columns and each gird with a number.We define sumBlack is the sum of all Black gird and sumWhite is the sum of all White gird.
You are to calculate how many ways there are to fill the remaining part of the grid under the constraints stated below to make the absolute of (sumBlack - sumWhite) minimum and output one of these ways (if any exist).
Each cell in the grid should be colored either black or white.
All black cells in the grid should be connected with each other, and all white cells should also be connected with each other.The pictures below show two filled grids where this constraint is only fulfilled in the picture2.

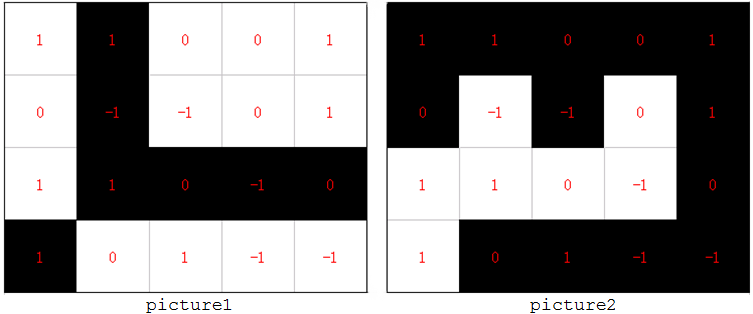
There must be no 2x2 blocks in the grid which consists of only white cells, or of only black cells.
The picture3 shows a grid with a black and a white 2x2 block, while the picture4 contains no such 2x2 block.

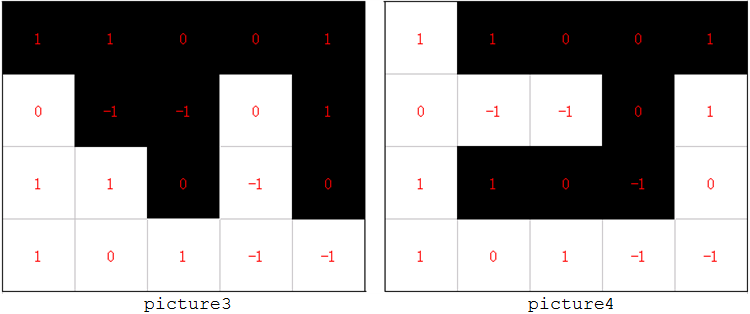
You are not allowed to change the color of any of the cells whose color has already been assigned in the input, and all cells must be colored.

 

Input

The first line in the input contains an integer T (1<=T<=30), the number of cases to follow.
Each case starts with two integers, N and M (2 ≤ N, M ≤ 8), the number of rows and columns respectively in the grid.
The next N lines contains M characters each and describes the grid using the following characters:
  # - a cell which is colored black
  o - a cell which is colored white
  . - a cell which color has not yet been assigned
The next N lines contains M integers (-1 or 0 or 1) each indicating the number of this gird.

 

Output

For each case, first line output the number of case(as shown in the sample output)
If there are at least one way, then output the minimum absolute of (sumBlack - sumWhite) and the number of ways to fill the grid make it minimum in a line and output one of these ways, using the same format for the grid as in the input.(anyone is ok)
If there is no way to fill the gird under the constraints stated , just output two zero.
Output a blank line after each case.(Special judge.If you not output a blank line after each case, you may get Wrong Answer)

 

Sample Input

4 2 3 xxx oox 1 1 0 0 1 0 2 3 ... ... 1 1 0 0 1 -1 5 5 ..x.. ..... ....o o.... .x... 1 1 0 0 1 0 -1 -1 0 1 1 1 0 -1 0 1 0 1 -1 -1 -1 -1 1 -1 0 4 5 ..... ..... ..... ..... 1 1 0 0 1 0 -1 -1 0 1 1 1 0 -1 0 1 0 1 -1 -1

 

Sample Output

Case 1: 1 1 xxx oox Case 2: 0 8 xxx xox Case 3: 0 0 Case 4: 1 54 xxxxx xoxox oooox oxxxx

 

---

转移状态较多，给出胡浩的题解：

 然后注意一点，他这个轮廓线不包括左右插头的轮廓线，也就是只包含上下插头的轮廓线，所以只有m个。

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#define clr(x) memset(x,0,sizeof(x))
#define clr_1(x) memset(x,-1,sizeof(x))
#define LL long long
#define HASH 100003
#define STATE 100010
#define INF 0x3f3f3f3f
using namespace std;
char s[10][10];
int value[10][10];
int pre[65][100010];
char sta[65][100010];
int code[10],ch[10];
int n,m;
struct hashmap//hash表存状态及大的数和
{
    int size;
    int next[STATE],head[HASH];
    int state[STATE],dif[STATE],col[STATE];
    LL fas[STATE];
    void init()//清空
    {
        size=0;
        clr_1(head);
    }
    void add(int st,int difr,int colr,int prer,char chr,LL solu,int id)
    {
        int k=((st<<6)+colr+difr+2000)%HASH;
        for(int i=head[k];i!=-1;i=next[i])
        if(st==state[i] && difr==dif[i] && colr==col[i])
        {
            fas[i]+=solu;
            return ;
        }
        state[++size]=st;
        dif[size]=difr;
        col[size]=colr;
        fas[size]=solu;
        pre[id][size]=prer;
        sta[id][size]=chr;
        next[size]=head[k];
        head[k]=size;
        return ;
    }
}dp[2];
void init(int n,int m)
{
    for(int i=0;i<n;i++)
        scanf("%s",s[i]);
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
            scanf("%d",&value[i][j]);
    return ; 
}
int encode(int *code,int m)
{
    int st=0;
    clr_1(ch);
    int ct=-1;
    for(int i=0;i<m;i++)
    {
           st<<=3;
        if(ch[code[i]]==-1) ch[code[i]]= ++ ct;
        st=st|ch[code[i]];
    }
    return st;
}
void decode(int *code,int m,int st)
{
    for(int i=m-1;i>=0;i--)
    {
        code[i]=st & 7;
        st>>=3;
    }
    return ;
}
void print(int k)
{
    for(int i=n-1;i>=0;i--)
        for(int j=m-1;j>=0;j--)
        {
            s[i][j]=sta[i*m+j][k];
            k=pre[i*m+j][k];
        }
    for(int i=0;i<n;i++)
        printf("%s
",s[i]);
    return ;
}
void dpblank(int i,int j,int cnt,int c)
{
    int lt,up,ltup,col,s1,s2;
    for(int it=1;it<=dp[cnt].size;it++)
    {
        decode(code,m,dp[cnt].state[it]);
        col=dp[cnt].col[it];
        up=(i>0)?(col>>j&1)==c:0;
        lt=(j>0)?(col>>(j-1) & 1)==c:0;
        ltup=(i&&j)?(col >> m)==c:0;
        if(i==n-1 && j==m-1 && !lt & !up & ltup) continue;
        if(lt && up && ltup) continue;
        if(i && !up)
        {
            s1=s2=0;
            for(int k=0;k<m;k++)
            {
                if(code[k]==code[j])
                    s1++;
                if((col>>k&1)!=c)
                    s2++;
            }
            if(s1==1)
            {
                if(s2>1) continue;
                if(i<n-1 || j<m-2) continue;
            }
        }
        if(lt && up)
        {
            if(code[j]!=code[j-1])
                for(int k=0,x=code[j];k<m;k++)
                    if(code[k]==x)
                        code[k]=code[j-1];
        }
        else if(lt & !up)
            code[j]=code[j-1];
        else if(!lt && !up)
            code[j]=m;
        if(col & 1 << j) col |= 1 << m;
        else col &= ~(1 << m);
        if(c) col |= 1 << j;
        else col &= ~(1 << j);
        dp[cnt^1].add(encode(code,m),dp[cnt].dif[it]+ (c ? -value[i][j] : value[i][j]),col,it,(c==0?'o':'x'),dp[cnt].fas[it],i*m+j);
    }
    return ;
}
void solve(int n,int m)
{
    int cnt=0;
    dp[cnt].init();
    dp[cnt].add(0,0,0,0,0,1,0);
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
        {
            dp[cnt^1].init();
            if(s[i][j]!='x') dpblank(i,j,cnt,0);
            if(s[i][j]!='o') dpblank(i,j,cnt,1);
            cnt^=1; 
        };
    int minx=INF,ctk;
    LL ans=0;
    int ct;
    for(int it=1;it<=dp[cnt].size; it++)
    {
        int s1 = 0;
        clr(ch);
        decode(code,m,dp[cnt].state[it]);
        for(int j = 0; j < m; j ++) if(!ch[code[j]]) ++s1, ch[code[j]] = 1;
        if(s1 <= 2)
        {
            if(abs(dp[cnt].dif[it]) < minx)
                minx=abs(dp[cnt].dif[it]),ans = dp[cnt].fas[it],ctk=it;
            else if(abs(dp[cnt].dif[it])==minx)
                ans+=dp[cnt].fas[it];    
        }
    }
    if(minx==INF) printf("0 0
");
    else
    {
        printf("%d %lld
", minx,ans);
        print(ctk);
    }
    return ;
}
int main()
{
    int T;
    scanf("%d",&T);
    for(int kase=1;kase<=T;kase++)
    {
        scanf("%d%d",&n,&m);
        init(n,m);
        printf("Case %d: ",kase);
        solve(n,m);
        printf("
");
    }
    return 0;
}