选择排序------堆排序

堆排序与快速排序，归并排序一样都是时间复杂度为O(N*logN)的几种常见排序方法。

堆排序有点类似选择排序，都是每次选出最大的数或最小的数。

对于堆，由于其根节点为堆中最大的节点，因此每次只需取出其根节点，然后重新建堆，再重复前面操作

故按如下步骤：

　　首先可以看到堆建好之后堆中第0个数据是堆中最大的数据。取出这个数据再执行下堆的删除操作。这样堆中第0个数据又是堆中最大的数据，重复上述步骤直至堆中只有一个数据时就直接取出这个数据。

　　由于堆也是用数组模拟的，故堆化数组后，第一次将A[0]与A[n - 1]交换，再对A[0…n-2]重新恢复堆。第二次将A[0]与A[n – 2]交换，再对A[0…n - 3]重新恢复堆，重复这样的操作直到A[0]与A[1]交换。由于每次都是将最小的数据并入到后面的有序区间，故操作完成后整个数组就有序了。

     在前面介绍了对的删除，插入和建堆等操作（加了哨兵，数组从第1个元素开始），下面实现堆排序。

#include <iostream>

using namespace std;

struct  Heap_Struct{
     int *Element;
     int size;
     int capacity;
};

void Heap_Sort(void); 
Heap_Struct*  Heap_Construct(int *arr,int len);
int Heap_Delete(Heap_Struct *h);

int main()
{
    Heap_Sort( );
    return 0;
}

Heap_Struct*  Heap_Construct(int *arr,int len)
{/*根据长度为len的数组创建最大堆*/
    
      Heap_Struct  *H_tmp= new Heap_Struct;
      H_tmp->Element=new int[len+1];
      H_tmp->size=len;
      H_tmp->capacity=len;

      int i,start,tmp=0;
      int parent,child;
      for (i=1;i<len+1;i++)
        {
            H_tmp->Element[i]=arr[i-1];
            if(tmp<arr[i])
                tmp=arr[i];
        }
      H_tmp->Element[0]=tmp+5;  
      start=i/2;
      for(i=start;i>0;i--)
      {
           parent=i;
            while(2*parent<=H_tmp->size)  //存在子节点 
         {
            if(2*parent+1<=len && H_tmp->Element[2*parent+1]>H_tmp->Element[2*parent] && H_tmp->Element[2*parent+1]>H_tmp->Element[parent])
            {
                   tmp=H_tmp->Element[parent];
                   H_tmp->Element[parent]=H_tmp->Element[2*parent+1];
                   H_tmp->Element[2*parent+1]=tmp;      
                   parent=2*parent+1;
            }
           else if(H_tmp->Element[2*parent]>H_tmp->Element[parent])
            {
                    tmp=H_tmp->Element[parent];
                    H_tmp->Element[parent]=H_tmp->Element[2*parent];
                    H_tmp->Element[2*parent]=tmp; 
                    parent=2*parent;      
            }
           else 
               break;
         }
      }
       return H_tmp;
}        

int Heap_Delete(Heap_Struct *h)
{
     int MaxData=h->Element[1];
     int tmp=h->Element[h->size--];/*取出最后一个元素并将堆的长度减1*/
     int i=1;
     while(2*i<=h->size && h->Element[2*i]>tmp)
     {
            if((2*i+1)<=h->size && h->Element[2*i+1]>h->Element[2*i] && h->Element[2*i+1]>tmp)  /*右节点存在且大于左节点且大于插入的值，则将右节点移到其父节点并继续向上过滤*/
           { 
                    h->Element[i]=h->Element[2*i+1];;
                    i=2*i+1;
           }
            else if(h->Element[2*i]>tmp)   /*左节点大且大于插入的值，则将左节点移到其父节点并继续向上过滤*/
           {
                   h->Element[i]=h->Element[2*i];
                   i=2*i;
            }
            else
                   break;
     }

        h->Element[i]=tmp;   /*将最后一个数插到堆中*/
      return MaxData;
}                      

void Heap_Sort(void)
{
    int arr[]={79,66,43,83,30,87,38,55,91,72,49,9};
    int len=12;
    cout <<"原始数据："; 
    for(int i=0;i<len;i++)
        cout << arr[i] <<' ';
    cout << endl;
    
    Heap_Struct* h=Heap_Construct(arr,len); //建堆
    
    cout <<"堆中数据：";
    for(int i=1;i<len+1;i++)
        cout << h->Element[i] << ' ';
    cout <<endl;
    
    for(int i=0;i<len;i++)                 //循环删除堆的根节点，并将其插入到数组的末尾 
        arr[len-i-1]=Heap_Delete(h);
    
    cout <<"排序后数据：" ;
    for(int i=0;i<12;i++)
        cout << arr[i] <<' ';
    cout <<endl;
}

结果为：

　　

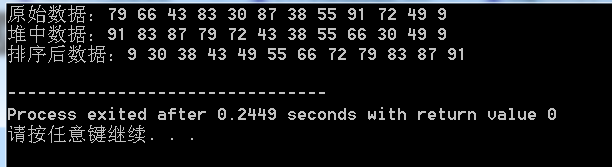
　　由于每次重新恢复堆的时间复杂度为O(logN)，共N - 1次重新恢复堆操作，再加上前面建立堆时N / 2次向下调整，每次调整时间复杂度也为O(logN)。二次操作时间相加还是O(N * logN)。故堆排序的时间复杂度为O(N * logN)。STL也实现了堆的相关函数，可以参阅《STL系列之四 heap 堆》。