二叉树

①二叉树的定义：二叉树是由n(n>=0)个结点组成的有限集合，该集合或者为空，或者是由一个根结点加上两颗分别称为左子树和右子树的、互不相交的二叉树组成

②二叉树的五种不同形态：

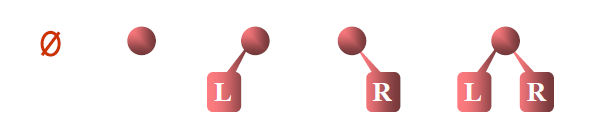
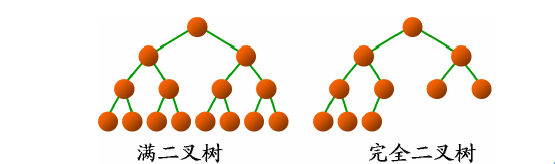
③满二叉树（Full Binary Tree）：如果二叉树中的所有分支结点的度数都为二，且叶子结点都在同一层上，则称这类二叉树为满二叉树

④完全二叉树 （Complete Binary Tree）：如果一个具有n个结点的高度为k的二叉树，它的每一个结点都与高度为k的满二叉树中的编号为1-n的结点一一对应，则称这颗二叉树为完全二叉树

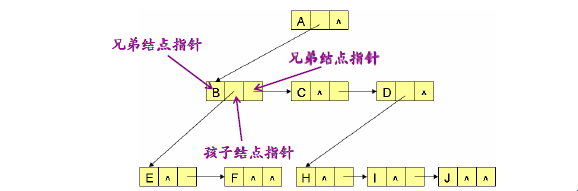
⑤孩子兄弟表示法能够将任意形状的树转换为二叉树

⑥二叉树的深层性质

性质1： 在二叉树的第i层最多有2^i-1个结点（i>=1）

性质2： 深度为k的二叉树最多有2^k-1个结点（k>=0）

性质3： 对任何一棵二叉树，如果其叶结点有n₀个，度数为2的非叶结点有n₂个，则: n = n + 1 

性质4：具有n个结点的完全二叉树的高度为|log₂n| + 1（|x|表示不大于x的整数）|log 2 n|+1 |log2⁡n|+1

（其中|x|表示不大于x的最大整数）。

性质5：一棵有n个结点的二叉树（高度为|log₂n| + 1），按层次对结点进行编号（从上到下，从左到右），对任意结点i有：

如果i=1，则结点i是二叉树的根

如果i>1，则其双亲结点为|i/2|

如果2i<=n，则结点i的左孩子为2i

如果2i>n，则结点i无左孩子

如果2i+1<=n，则结点i的右孩子为2i+1

如果2i+1>n，则结点i无右孩子

⑦指路法创建二叉树（非递归方式）

1.指路法通过根结点与目标结点的相对位置进行定位，可以避开二叉树的递归性质而“线性”定位

2.二叉树的存储结构

结点指针域定义：

typedef struct _BTreeNode BTreeNode;
struct _BTreeNode
{
    BTreeNode* left;
    BTreeNode* right;
};

头结点定义：

typedef struct _BTree BTree;
struct _BTree
{
    int count;
    BTreeNode* root;
};

数据元素定义：

struct Node
{
    BTreeNode header;
    char v;
};