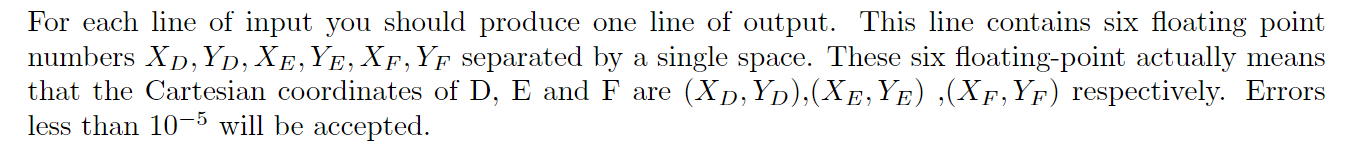UVA 11178 Morley's Theorem (坐标旋转)

题目链接：UVA 11178

Description

Input

Output

Sample Input

Sample Output

Solution

题意

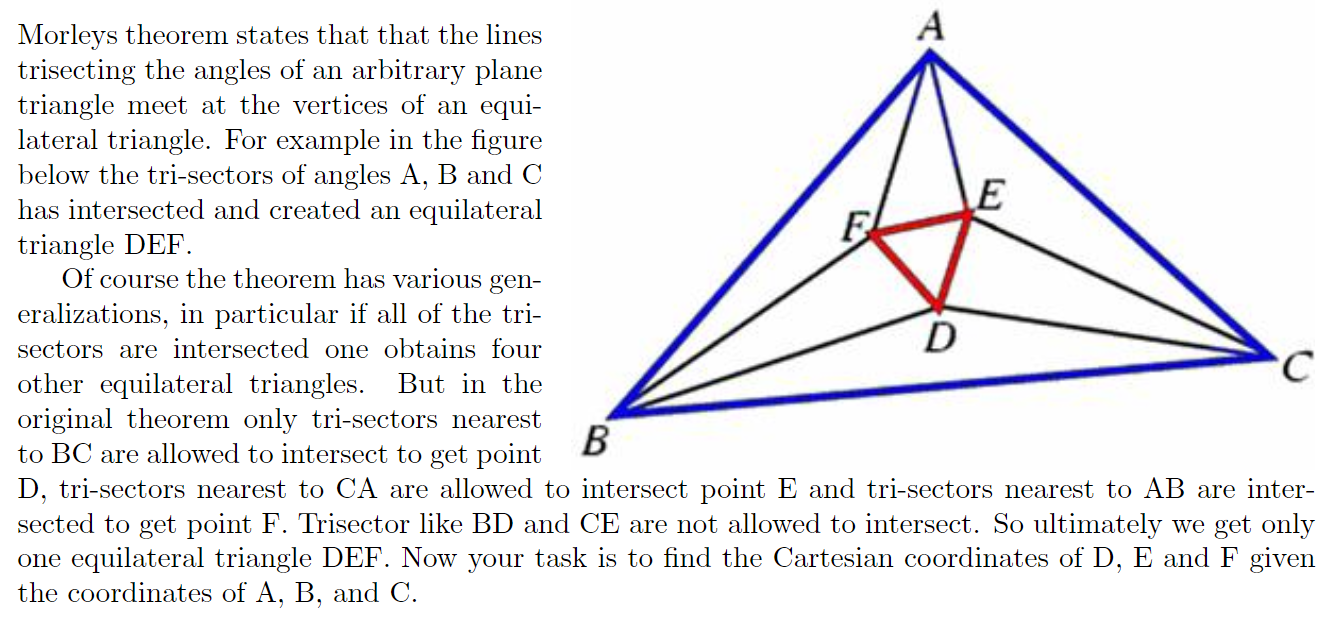
(Morley's theorem) 指任意三角形的每个内角的三等分线相交的三角形为等边三角形。

给出三角形的每个点的坐标，求根据 (Morley's theorem) 构造的等边三角形的三个点的坐标。

题解

对于点 (D)，只需求直线 (BC) 绕点 (B) 旋转 (frac{1}{3} angle ABC) 的直线与直线 (CB) 绕点 (C) 旋转 (frac{1}{3} angle ACB) 的直线的交点。其他两点类似。

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
const db eps = 1e-10;
const db pi = acos(-1.0);
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll maxn = 1e5 + 10;

inline int dcmp(db x) {
    if(fabs(x) < eps) return 0;
    return x > 0? 1: -1;
}

class Point {
public:
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) {}
    void input() {
        scanf("%lf%lf", &x, &y);
    }
    Point operator+(const Point a) {
        return Point(x + a.x, y + a.y);
    }
    Point operator-(const Point a) {
        return Point(x - a.x, y - a.y);
    }
    bool operator<(const Point &a) const {
        return (!dcmp(y - a.y))? dcmp(x - a.x) < 0: y < a.y;
    }
    db dis2() {
        return x * x + y * y;
    }
    db dis() {
        return sqrt(dis2());
    }
    db dot(const Point a) {
        return x * a.x + y * a.y;
    }
    db cross(const Point a) {
        return x * a.y - y * a.x;
    }
    db ang(Point a) {
        return acos(dot(a) / (a.dis() * dis()));
    }
    Point Rotate(double rad) {
        return Point(x * cos(rad) - y * sin(rad), x * sin(rad) + y * cos(rad));
    }
};
typedef Point Vector;

class Line {
public:
    Point s, e;
    db angle;
    Line() {}
    Line(Point s, Point e) : s(s), e(e) {}
    inline void input() {
        scanf("%lf%lf%lf%lf", &s.x, &s.y, &e.x, &e.y);
    }
    int toLeftTest(Point p) {
        if((e - s).cross(p - s) > 0) return 1;
        else if((e - s).cross(p - s) < 0) return -1;
        return 0;
    }
    Point crosspoint(Line l) {
		double a1 = (l.e - l.s).cross(s - l.s);
		double a2 = (l.e - l.s).cross(e - l.s);
        double x = (s.x * a2 - e.x * a1) / (a2 - a1);
        double y = (s.y * a2 - e.y * a1) / (a2 - a1);
        if(dcmp(x) == 0) x = 0;
        if(dcmp(y) == 0) y = 0;
		return Point(x, y);
	}
};

Point get_crosspoint(Point A, Point B, Point C) {
    Vector v1 = C - B;
    db a1 = v1.ang(A - B);
    v1 = v1.Rotate(a1 / 3.0);
    v1 = v1 + B;
    Vector v2 = B - C;
    db a2 = v2.ang(A - C);
    v2 = v2.Rotate(-a2 / 3.0);
    v2 = v2 + C;
    Line l1 = Line(B, v1);
    Line l2 = Line(C, v2);
    return l1.crosspoint(l2); 
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        Point a, b, c;
        a.input(); b.input(); c.input();
        Point d, e, f;
        d = get_crosspoint(a, b, c);
        e = get_crosspoint(b, c, a);
        f = get_crosspoint(c, a, b);
        printf("%.6lf %.6lf %.6lf %.6lf %.6lf %.6lf
", d.x, d.y, e.x, e.y, f.x, f.y);
    }
    return 0;
}