Description
Let's define logical OR as an operation on two logical values (i. e. values that belong to the set {0, 1}) that is equal to 1 if either or both of the logical values is set to 1, otherwise it is 0. We can define logical OR of three or more logical values in the same manner:
 where
where 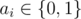 is equal to 1 if some ai = 1, otherwise it is equal to 0.
is equal to 1 if some ai = 1, otherwise it is equal to 0.
Nam has a matrix A consisting of m rows and n columns. The rows are numbered from 1 to m, columns are numbered from 1 to n. Element at row i (1 ≤ i ≤ m) and column j (1 ≤ j ≤ n) is denoted as Aij. All elements of A are either 0 or 1. From matrix A, Nam creates another matrix B of the same size using formula:
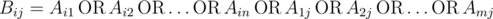 .
.
(Bij is OR of all elements in row i and column j of matrix A)
Nam gives you matrix B and challenges you to guess matrix A. Although Nam is smart, he could probably make a mistake while calculating matrix B, since size of A can be large.
Input
The first line contains two integer m and n (1 ≤ m, n ≤ 100), number of rows and number of columns of matrices respectively.
The next m lines each contain n integers separated by spaces describing rows of matrix B (each element of B is either 0 or 1).
Output
In the first line, print "NO" if Nam has made a mistake when calculating B, otherwise print "YES". If the first line is "YES", then also print m rows consisting of n integers representing matrix A that can produce given matrix B. If there are several solutions print any one.
Sample Input
2 2
1 0
0 0
NO
2 3
1 1 1
1 1 1
YES
1 1 1
1 1 1
2 3
0 1 0
1 1 1
YES
0 0 0
0 1 0
/* 题意:定义一个异或,a1^a2...^an如果有一个ai=1那么值为1,否则为零,给出你一个矩阵B,是由矩阵A得来的,Bij等于A的i行元素 异或j列元素。给出你矩阵B问你是否有这样的矩阵A 初步思路:将矩阵初始化为1,然后先按照矩阵B中有零的元素,将对应A矩阵中的元素设置成零,然后在反过来验证B矩阵 */ #include <bits/stdc++.h> using namespace std; int n,m; int a[110][110]; int b[110][110]; int main(){ // freopen("in.txt","r",stdin); scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ scanf("%d",&b[i][j]); a[i][j]=1; } } //按照B矩阵进行置0 for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ if(b[i][j]==0){ for(int k=1;k<=m;k++) a[i][k]=0; for(int k=1;k<=n;k++) a[k][j]=0; } } } //验证然后按照1的位置验证B矩阵 bool f=false; for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ if(b[i][j]==1){ bool flag=false; for(int k=1;k<=n;k++){ if(a[i][k]==1){ flag=true; break; } } if(flag==false) for(int k=1;k<=m;k++){ if(a[k][j]==1){ flag=true; break; } } if(flag==false){ f=true; break; } } } } if(f){ puts("NO"); }else{ puts("YES"); for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ printf(j==1?"%d":" %d",a[i][j]); } printf(" "); } } return 0; }