PCA算法和SVD

如果矩阵对某一个向量或某些向量只发生伸缩变换，不对这些向量产生旋转的效果，那么这些向量就称为这个矩阵的特征向量，伸缩的比例就是特征值。这里可以将特征值为负，特征向量旋转180度，也可看成方向不变，伸缩比为负值。所以特征向量也叫线性不变量

PCA的物理意义：

各种不同的信号（向量）进入这个系统中后，系统输出的信号（向量）就会发生相位滞后、放大、缩小等各种纷乱的变化。但只有特征信号（特征向量）被稳定的发生放大（或缩小）的变化。如果把系统的输出端口接入输入端口，那么只有特征信号（特征向量）第二次被放大（或缩小）了，其他的信号如滞后的可能滞后也可能超前

这个系统的物理特性就可以被这个矩阵的特征值所决定，这个矩阵能形成“频率的谱

脑补部分：

 

2. PCA计算过程

     首先介绍PCA的计算过程：

     假设我们得到的2维数据如下：

     

     行代表了样例，列代表特征，这里有10个样例，每个样例两个特征。可以这样认为，有10篇文档，x是10篇文档中“learn”出现的TF-IDF，y是10篇文档中“study”出现的TF-IDF。也可以认为有10辆汽车，x是千米/小时的速度，y是英里/小时的速度，等等。

     第一步分别求x和y的平均值，然后对于所有的样例，都减去对应的均值。这里x的均值是1.81，y的均值是1.91，那么一个样例减去均值后即为（0.69,0.49），得到

     

     第二步，求特征协方差矩阵，如果数据是3维，那么协方差矩阵是

     

     这里只有x和y，求解得

     

     对角线上分别是x和y的方差，非对角线上是协方差。协方差大于0表示x和y若有一个增，另一个也增；小于0表示一个增，一个减；协方差为0时，两者独立。协方差绝对值越大，两者对彼此的影响越大，反之越小。

     第三步，求协方差的特征值和特征向量，得到

     

     上面是两个特征值，下面是对应的特征向量，特征值0.0490833989对应特征向量为，这里的特征向量都归一化为单位向量。

    第四步，将特征值按照从大到小的顺序排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。

     这里特征值只有两个，我们选择其中最大的那个，这里是1.28402771，对应的特征向量是。

     第五步，将样本点投影到选取的特征向量上。假设样例数为m，特征数为n，减去均值后的样本矩阵为DataAdjust(m*n)，协方差矩阵是n*n，选取的k个特征向量组成的矩阵为EigenVectors(n*k)。那么投影后的数据FinalData为

     

     这里是

     FinalData(10*1) = DataAdjust(10*2矩阵)×特征向量

     得到结果是

     

     这样，就将原始样例的n维特征变成了k维，这k维就是原始特征在k维上的投影。

     上面的数据可以认为是learn和study特征融合为一个新的特征叫做LS特征，该特征基本上代表了这两个特征。

 

SVD一般是用来诊断两个场的相关关系的，而PCA是用来提取一个场的主要信息的（即主分量）。两者在具体的实现方法上也有不同，SVD是通过矩阵奇异值分解的方法分解两个场的协方差矩阵的（两个场的维数不同，不对称），而PCA是通过Jacobi方法分解一个场的协方差矩阵（T'*T).

 

    但是这个怎么和SVD扯上关系呢？之前谈到，SVD得出的奇异向量也是从奇异值由大到小排列的，按PCA的观点来看，就是方差最大的坐标轴就是第一个奇异向量，方差次大的坐标轴就是第二个奇异向量…我们回忆一下之前得到的SVD式子：

     在矩阵的两边同时乘上一个矩阵V，由于V是一个正交的矩阵，所以V转置乘以V得到单位阵I，所以可以化成后面的式子

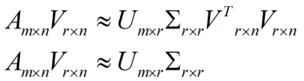     将后面的式子与A * P那个m * n的矩阵变换为m * r的矩阵的式子对照看看，在这里，其实V就是P，也就是一个变化的向量。这里是将一个m * n 的矩阵压缩到一个m * r的矩阵，也就是对列进行压缩，如果我们想对行进行压缩（在PCA的观点下，对行进行压缩可以理解为，将一些相似的sample合并在一起，或者将一些没有太大价值的sample去掉）怎么办呢？同样我们写出一个通用的行压缩例子：

    这样就从一个m行的矩阵压缩到一个r行的矩阵了，对SVD来说也是一样的，我们对SVD分解的式子两边乘以U的转置U'

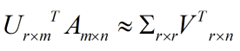    这样我们就得到了对行进行压缩的式子。可以看出，其实PCA几乎可以说是对SVD的一个包装，如果我们实现了SVD，那也就实现了PCA了，而且更好的地方是，有了SVD，我们就可以得到两个方向的PCA，如果我们对A’A进行特征值的分解，只能得到一个方向的PCA。

以下也是来自别人的一个博客：

实际使用

用sklearn封装的PCA方法，做PCA的代码如下。PCA方法参数n_components，如果设置为整数，则n_components=k。如果将其设置为小数，则说明降维后的数据能保留的信息。

from sklearn.decomposition import PCA
import numpy as np
from sklearn.preprocessing import StandardScaler

x=np.array([[10001,2,55], [16020,4,11], [12008,6,33], [13131,8,22]])

# feature normalization (feature scaling)
X_scaler = StandardScaler()
x = X_scaler.fit_transform(x)

# PCA
pca = PCA(n_components=0.9)# 保证降维后的数据保持90%的信息
pca.fit(x)
pca.transform(x)

所以在实际使用PCA时，我们不需要选择k，而是直接设置n_components为float数据。

总结

PCA主成分数量k的选择，是一个数据压缩的问题。通常我们直接将sklearn中PCA方法参数n_components设置为float数据，来间接解决k值选取问题。 
但有的时候我们降维只是为了观测数据（visualization），这种情况下一般将k选择为2或3。

5. SVD用于PCA

　　　　在主成分分析（PCA）原理总结中，我们讲到要用PCA降维，需要找到样本协方差矩阵XTXXTX的最大的d个特征向量，然后用这最大的d个特征向量张成的矩阵来做低维投影降维。可以看出，在这个过程中需要先求出协方差矩阵XTXXTX，当样本数多样本特征数也多的时候，这个计算量是很大的。

　　　　注意到我们的SVD也可以得到协方差矩阵XTXXTX最大的d个特征向量张成的矩阵，但是SVD有个好处，有一些SVD的实现算法可以不求先求出协方差矩阵XTXXTX，也能求出我们的右奇异矩阵VV。也就是说，我们的PCA算法可以不用做特征分解，而是做SVD来完成。这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是我们我们认为的暴力特征分解。

　　　　另一方面，注意到PCA仅仅使用了我们SVD的右奇异矩阵，没有使用左奇异矩阵，那么左奇异矩阵有什么用呢？

　　　　假设我们的样本是m×nm×n的矩阵X，如果我们通过SVD找到了矩阵XXTXXT最大的d个特征向量张成的m×dm×d维矩阵U，则我们如果进行如下处理：

X′d×n=UTd×mXm×nXd×n′=Ud×mTXm×n

　　　　可以得到一个d×nd×n的矩阵X‘,这个矩阵和我们原来的m×nm×n维样本矩阵X相比，行数从m减到了k，可见对行数进行了压缩。也就是说，左奇异矩阵可以用于行数的压缩。相对的，右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的PCA降维。