基本概念和性质
在计算机科学中,trie,又称前缀树或字典树或单词搜索树,是一种有序树,用于保存关联数组,其中的键通常是字符串。与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
本文地址:http://www.cnblogs.com/archimedes/p/trie-tree.html,转载请注明源地址。
在图示中,键标注在节点中,值标注在节点之下。每一个完整的英文单词对应一个特定的整数。Trie 可以看作是一个确定有限状态自动机,尽管边上的符号一般是隐含在分支的顺序中的。键不需要被显式地保存在节点中。图示中标注出完整的单词,只是为了演示 trie 的原理。
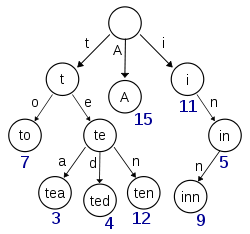
trie 中的键通常是字符串,但也可以是其它的结构。trie 的算法可以很容易地修改为处理其它结构的有序序列,比如一串数字或者形状的排列。比如,bitwise trie 中的键是一串位元,可以用于表示整数或者内存地址。
Trie树是一种树形结构,是一种哈希树的变种。典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:最大限度地减少无谓的字符串比较,查询效率比哈希表高。Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
它有3个基本性质:
(1) 根节点不包含字符,除根节点外每一个节点都只包含一个字符。
(2) 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
(3) 每个节点的所有子节点包含的字符都不相同。
基本思想(以字母树为例):
1、插入过程
对于一个单词,从根开始,沿着单词的各个字母所对应的树中的节点分支向下走,直到单词遍历完,将最后的节点标记为红色,表示该单词已插入Trie树。
2、查询过程
同样的,从根开始按照单词的字母顺序向下遍历trie树,一旦发现某个节点标记不存在或者单词遍历完成而最后的节点未标记为红色,则表示该单词不存在,若最后的节点标记为红色,表示该单词存在。
Trie树的实现
字母树的插入(Insert)、删除( Delete)和查找(Find)都非常简单,用一个一重循环即可,即第i 次循环找到前i个字母所对应的子树,然后进行相应的操作。实现这棵字母树,至于Trie树的实现,可以用数组,也可以用指针动态分配,平时为了方便就用数组,静态分配空间。
1、trie结构体
struct Trie { Trie *next[26]; bool isWord; }Root;
2、插入操作
//插入操作(也是构建Trie树) void insert(char *tar) { Trie* head = &Root; int id; while(*tar) { id = *tar - 'a'; if(head->next[id] == NULL) head->next[id] = new Trie(); head = head->next[id]; tar++; } head->isWord = true; }
3、查找操作
//查找 bool search(char *tar) { Trie* head = &Root; int id; while(*tar) { id = *tar - 'a'; if(head->next[id] == NULL) return false; head = head->next[id]; tar++; } if(head->isWord) return true; else return false; }
至于结点对儿子的指向,一般有三种方法:
1、对每个结点开一个字母集大小的数组,对应的下标是儿子所表示的字母,内容则是这个儿子对应在大数组上的位置,即标号;
2、对每个结点挂一个链表,按一定顺序记录每个儿子是谁;
3、使用左儿子右兄弟表示法记录这棵树。
三种方法,各有特点。第一种易实现,但实际的空间要求较大;第二种,较易实现,空间要求相对较小,但比较费时;第三种,空间要求最小,但相对费时且不易写。
下面给出动态开辟内存的实现:
#define MAX_NUM 26 enum NODE_TYPE{ //"COMPLETED" means a string is generated so far. COMPLETED, UNCOMPLETED }; struct Node { enum NODE_TYPE type; char ch; struct Node* child[MAX_NUM]; //26-tree->a, b ,c, .....z }; struct Node* ROOT; //tree root struct Node* createNewNode(char ch){ // create a new node struct Node *new_node = (struct Node*)malloc(sizeof(struct Node)); new_node->ch = ch; new_node->type == UNCOMPLETED; int i; for(i = 0; i < MAX_NUM; i++) new_node->child[i] = NULL; return new_node; } void initialization() { //intiazation: creat an empty tree, with only a ROOT ROOT = createNewNode(' '); } int charToindex(char ch) { //a "char" maps to an index<br> return ch - 'a'; } int find(const char chars[], int len) { struct Node* ptr = ROOT; int i = 0; while(i < len) { if(ptr->child[charToindex(chars[i])] == NULL) { break; } ptr = ptr->child[charToindex(chars[i])]; i++; } return (i == len) && (ptr->type == COMPLETED); } void insert(const char chars[], int len) { struct Node* ptr = ROOT; int i; for(i = 0; i < len; i++) { if(ptr->child[charToindex(chars[i])] == NULL) { ptr->child[charToindex(chars[i])] = createNewNode(chars[i]); } ptr = ptr->child[charToindex(chars[i])]; } ptr->type = COMPLETED; }
Trie树的应用
Trie是一种非常简单高效的数据结构,但有大量的应用实例。
(1) 字符串检索
事先将已知的一些字符串(字典)的有关信息保存到trie树里,查找另外一些未知字符串是否出现过或者出现频率。
举例:
1、给出N个单词组成的熟词表,以及一篇全用小写英文书写的文章,请你按最早出现的顺序写出所有不在熟词表中的生词。
2、给出一个词典,其中的单词为不良单词。单词均为小写字母。再给出一段文本,文本的每一行也由小写字母构成。判断文本中是否含有任何不良单词。例如,若rob是不良单词,那么文本problem含有不良单词。
(2)字符串最长公共前缀
Trie树利用多个字符串的公共前缀来节省存储空间,反之,当我们把大量字符串存储到一棵trie树上时,我们可以快速得到某些字符串的公共前缀。
举例:
给出N 个小写英文字母串,以及Q 个询问,即询问某两个串的最长公共前缀的长度是多少?
解决方案:首先对所有的串建立其对应的字母树。此时发现,对于两个串的最长公共前缀的长度即它们所在结点的公共祖先个数,于是,问题就转化为了离线(Offline)的最近公共祖先(Least Common Ancestor,简称LCA)问题。
而最近公共祖先问题同样是一个经典问题,可以用下面几种方法:
1. 利用并查集(Disjoint Set),可以采用采用经典的Tarjan 算法;
2. 求出字母树的欧拉序列(Euler Sequence )后,就可以转为经典的最小值查询(Range Minimum Query,简称RMQ)问题了;
(3)排序
Trie树是一棵多叉树,只要先序遍历整棵树,输出相应的字符串便是按字典序排序的结果。
举例:
给你N 个互不相同的仅由一个单词构成的英文名,让你将它们按字典序从小到大排序输出。
(4) 作为其他数据结构和算法的辅助结构
如后缀树,AC自动机等
字典树基本模板
#define MAX 26 //字符集大小 typedef struct TrieNode { int nCount; //记录该字符出现次数 struct TrieNode *next[MAX]; }TrieNode; TrieNode Memory[1000000]; int allocp = 0; /*初始化*/ void InitTrieRoot(TrieNode **pRoot) { *pRoot = NULL; } /*创建新结点*/ TrieNode *CreateTrieNode() { int i; TrieNode *p; p = &Memory[allocp++]; p->nCount = 1; for(i = 0 ; i < MAX ; i++) p->next[i] = NULL; return p; } /*插入*/ void InsertTrie(TrieNode **pRoot , char *s) { int i , k; TrieNode *p; if(!(p = *pRoot)) p = *pRoot = CreateTrieNode(); i = 0; while(s[i]) { k = s[i++] - 'a'; //确定branch if(p->next[k]) p->next[k]->nCount++; else p->next[k] = CreateTrieNode(); p = p->next[k]; } } //查找 int SearchTrie(TrieNode **pRoot , char *s) { TrieNode *p; int i , k; if(!(p = *pRoot)) return 0; i = 0; while(s[i]) { k = s[i++] - 'a'; if(p->next[k] == NULL) return 0; p = p->next[k]; } return p->nCount; }