逻辑斯蒂回归（Logistic Regression）理解及相关问题

逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法，运用梯度下降来求解参数，来达到将数据二分类的目的。

 

逻辑斯蒂分布

  logistic回归其实不是线性回归求预测值的问题，而是二分类问题。首先我们的线性回归模型输出的预测值，是一个实际的数字，那么我们想将他部署到分类问题，就需要让输出值转换到0/1就可以了。这里引入一个新的函数sigmoid：图像是这样的：

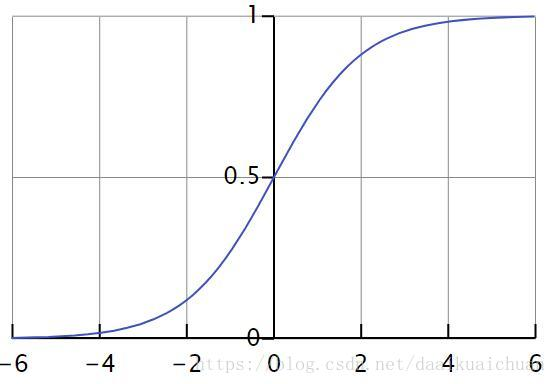
  此时我们将线性模型产生的预测值带入sigmoid函数，函数会输出相对应的二分类的概率，具体的训练方法和上面的线性回归是一样的，不同的是误差函数的求导

 

 

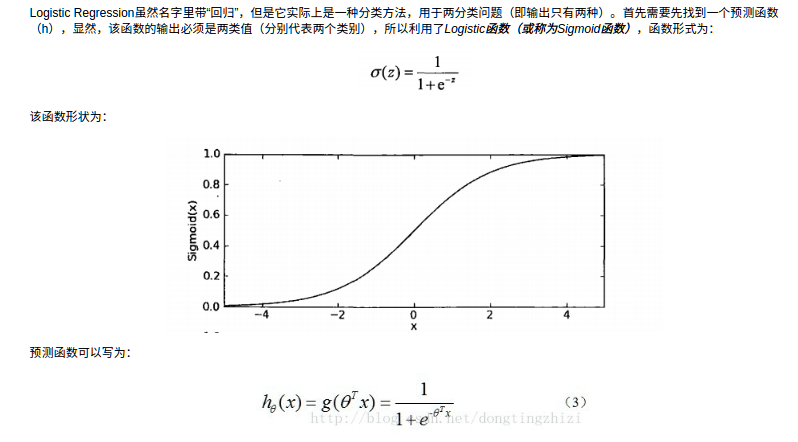
逻辑斯蒂回归算法的优缺点

1、优点

1. 形式简单，模型的可解释性非常好。从特征的权重可以看到不同的特征对最后结果的影响，某个特征的权重值比较高，那么这个特征最后对结果的影响会比较大；

2. 模型效果不错。在工程上是可以接受的（作为baseline)，如果特征工程做的好，效果不会太差，并且特征工程可以大家并行开发，大大加快开发的速度；

3. 训练速度较快。分类的时候，计算量仅仅只和特征的数目相关。并且逻辑回归的分布式优化sgd发展比较成熟，训练的速度可以通过堆机器进一步提高，这样我们可以在短时间内迭代好几个版本的模型；

4. 资源占用小,尤其是内存。因为只需要存储各个维度的特征值；

5. 方便输出结果调整。逻辑回归可以很方便的得到最后的分类结果，因为输出的是每个样本的概率分数，我们可以很容易的对这些概率分数进行cutoff，也就是划分阈值(大于某个阈值的是一类，小于某个阈值的是一类)。

2、缺点

1. 准确率并不是很高。因为形式非常的简单(非常类似线性模型)，很难去拟合数据的真实分布；

2. 很难处理数据不平衡的问题。举个例子：如果我们对于一个正负样本非常不平衡的问题比如正负样本比 10000:1.我们把所有样本都预测为正也能使损失函数的值比较小。但是作为一个分类器，它对正负样本的区分能力不会很好；

3. 处理非线性数据较麻烦。逻辑回归在不引入其他方法的情况下，只能处理线性可分的数据，或者进一步说，处理二分类的问题；

4. 逻辑回归本身无法筛选特征。有时候，我们会用gbdt来筛选特征，然后再上逻辑回归

逻辑斯蒂回归算法的相关问题

（1）逻辑斯蒂回归适合应用在什么场景？

　　在我们的工业应用上，如果需要作出分类的数据拥有很多有意义的特征，每个特征（我们假设这些特征都是有效的）都对最后的分类结果又或多或少的影响，那么最简单最有效的办法就是将这些特征线性加权，一起参与到作出决策的过程中。比如预测广告的点击率，又比如从原始数据集中筛选出符合某种要求的有用的子数据集。

　　逻辑斯蒂回归还有一个优点，那就是它不是硬性地将分类结果定为0或者1，而是给出了0和1之间的概率。这就相当于对每条数据的分类结果给出了一个打分。打分越高的数据越是我们想要的。如果我们要从一个数据集中筛选出一批数据（比如100个），就只要选出打分排名前100的数据就可以了。我们也可以根据实际情况设定一个阀值，大于这个阀值的归为一类，小于这个阀值的归为另一类。

logistic回归应用领域：

1. 用于二分类领域，可以得出概率值，适用于根据分类概率排名的领域，如搜索排名等；

2. Logistic回归的扩展softmax可以应用于多分类领域，如手写字识别等；

3. 信用评估；

4. 测量市场营销的成功度；

5. 预测某个产品的收益；

6. 特定的某天是否会发生地震。

（2）逻辑回归的损失函数为什么要使用极大似然函数作为损失函数？

 

  损失函数一般有四种，平方损失函数，对数损失函数，HingeLoss0-1损失函数，绝对值损失函数。将极大似然函数取对数以后等同于对数损失函数。在逻辑回归这个模型下，对数损失函数的训练求解参数的速度是比较快的。

  因为目标是要让预测为正的的概率最大，且预测为负的概率也最大，即每一个样本预测都要得到最大的概率，将所有的样本预测后的概率进行相乘都最大，这就能到似然函数了。

 

（3）逻辑回归在训练的过程当中，如果有很多的特征高度相关或者说有一个特征重复了100遍，会造成怎样的影响？

 

  如果在损失函数最终收敛的情况下，其实就算有很多特征高度相关也不会影响分类器的效果。

 

（4）为什么我们还是会在训练的过程当中将高度相关的特征去掉？

 

  去掉高度相关的特征会让模型的可解释性更好，可以大大提高训练的速度。如果模型当中有很多特征高度相关的话，就算损失函数本身收敛了，但实际上参数是没有收敛的，这样会拉低训练的速度。其次是特征多了，本身就会增大训练的时间。

 

（5）使用L1L2正则化，为什么可以降低模型的复杂度？

 

  模型越复杂，越容易过拟合，这大家都知道，加上L1正则化给了模型的拉普拉斯先验，加上L2正则化给了模型的高斯先验。从参数的角度来看，L1得到稀疏解，去掉一部分特征降低模型复杂度。L2得到较小的参数，如果参数很大，样本稍微变动一点，值就有很大偏差，这当然不是我们想看到的，相当于降低每个特征的权重。

 

（6）为什么L1能得到稀疏解呢？

 

  L1正则化是L1范数而来，投到坐标图里面，是棱型的，最优解在坐标轴上取到，所以某些部分的特征的系数就为0。

 

（7）L1正则化不可导，怎么求解？

 

  坐标轴下降法（按照每个坐标轴一个个使其收敛），最小角回归（是一个逐步的过程，每一步都选择一个相关性很大的特征，总的运算步数只和特征的数目有关，和训练集的大小无关）

参考文献：

https://blog.csdn.net/daaikuaichuan/article/details/80848958

http://blog.csdn.net/dongtingzhizi/article/details/15962797