树状数组 学习笔记

1.前置知识

二叉树。

分治。

前缀和。

2.树状数组

其实就是前缀和用二叉树做。

将二叉树右对齐即可。

如这样一颗二叉树

将它变成这样

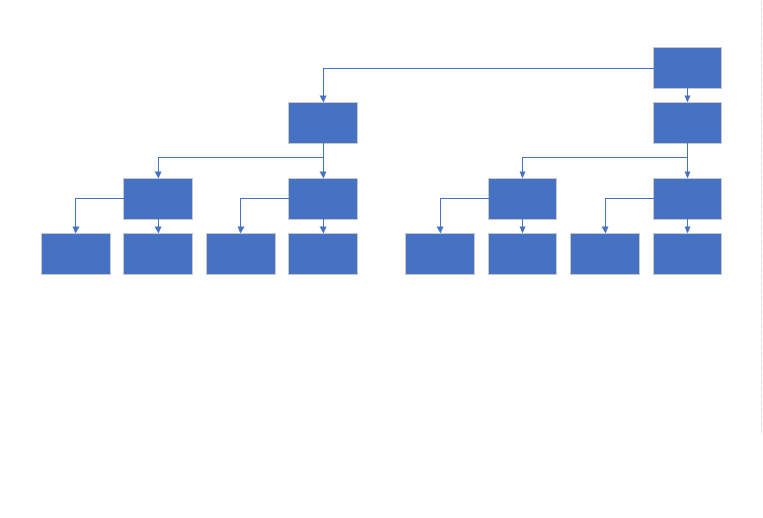
如下图（绿色为 (C) 数组，红色为 (a) 数组）

即(C_{1}=a_{1})

(\,\,\,\,\,\,C_{2}=a_{1}+a_{2})

(\,\,\,\,\,\,C_{3}=a_{3})

(\,\,\,\,\,\,C_{4}=a_{1}+a_{2}+a_{3}+a_{4})

(\,\,\,\,\,\,C_{5}=a_{5})

(\,\,\,\,\,\,C_{6}=a_{5}+a_{6})

(\,\,\,\,\,\,C_{7}=a_{7})

(\,\,\,\,\,\,C_{8}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+a_{6}+a_{7}+a_{8})

试试找规律？

全部转为二进制

0001	001
0010	001 010
0011	011
0100	001 010 011 100
0101	101
0110	101 110
0111	111
1000	001 010 011 100 101 110 111

不难发现 (C_{i}) 中数的个数为(2) 的 (i) 的二进制中 (1) 的最右边的位置后的 (0) 的个数 次幂。

读起来很绕口对吧，举个例子，如 ((0100)_{2})，它的最右边的 (1) 后有 (2) 个 (0)，(2^{2}=4)，所以 (C_{(0100)_{2}}) 中数的个数为 (4)。

那么问题来了，如何求 (i) 的二进制中最右边的 (1) 的位置呢？

给出如下代码

inline int lowbit(int x)
{
    return x&(-x);
}

解释一下。

-x 就是将 (x) 连同符号位一起反转再加一的结果，如 (0010) 的反码为 (1110)。

&运算 不用解释了吧。

运算x&(-x)，举个例子，(0101) 的反码为 (1011)，与 (0101) 进行 &运算 得 (0001) ，也就是 (1)，这就找到了 (i) 的二进制中最右边的 (1) 的位置。

3.单点更新，区间查询

inline void update(int x,int y)//表示将a[x]+y
{
    for(register int i=x;i<=n;i+=lowbit(i)) a[i]+=y;//每层更新
}

将每层与 (a_{x}) 相关的值更新一下。

inline int getsum(int x)//求C[x]的值
{
    ans=0;
    for(register int i=x;i;i-=lowbit(i)) ans+=a[i];
    return ans;
}

将每层与 (C_{x}) 相关的值相加求和。

然后用前缀和做就行啦。

即区间 ((x,y)) 的值为 getsum(y)-getsum(x-1)。

模板题1

模板题2

模板题3

仅给出 模板1 的代码（其实都差不多）。

#include<bits/stdc++.h>
using namespace std;
int ans;
int n,m;
int x,y,z;
int num;
int a[500002];
inline int read()
{
    int s=0,w=1;
    char ch=getchar();
    while(ch<'0'||ch>'9') {if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
    return s*w;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
inline void print(int x)
{
    write(x);
    putchar('
');
}
inline int lowbit(int x)
{
    return x&(-x);
}
inline void update(int x,int y)
{
    for(register int i=x;i<=n;i+=lowbit(i)) a[i]+=y;
}
inline int getsum(int x)
{
    ans=0;
    for(register int i=x;i;i-=lowbit(i)) ans+=a[i];
    return ans;
}
int main()
{
    n=read();m=read();
    for(register int i=1;i<=n;++i)
    {
        z=read();
        update(i,z);
    }
    for(register int i=1;i<=m;++i)
    {
        num=read();x=read();y=read();
        if(num==1) update(x,y);
            else print(getsum(y)-getsum(x-1));
    }
    return 0;
}

4.区间更新，单点查询

inline int lowbit(int x)
{
    return x&(-x);
}
inline void update(int x,int y)
{
    for(register int i=x;i<=n;i+=lowbit(i)) a[i]+=y;
}
inline int getsum(int x)
{
    ans=0;
    for(register int i=x;i;i-=lowbit(i)) ans+=a[i];
    return ans;
}

这些代码不会变。

多了个差分。

差分讲解一下。

有如下 (a) 数组

现在要将 ((2,5)) 这个区间里的值都加一。

直接循环复杂度肯定不优。

考虑将 (a_{2}+1,a_{5+1}-1)

即原数组为

这样在查询时可以定一个 (ans)，边循环边加，然后输出。

a[x]--,a[y+1]++ //差分

for i←1 to n+1
    do s+=a[i] //统计
       write(s,' ') //输出

( exttt{Q}):为何要这样差分？

( exttt{A}):在查询时将值赋为当前正确的值，在查询完减去即可。

于是可得差分代码

inline void add(int l,int r,int x)//对(l,r)的区间进行差分
{
    update(l,x);update(r+1,-x);
}
//（应该不难理解吧）

模板题

直接贴代码。

#include<bits/stdc++.h>
using namespace std;
int ans;
int n,m;
int x,y,k;
int now,last;
int num;
int a[500002];
inline int read()
{
    int s=0,w=1;
    char ch=getchar();
    while(ch<'0'||ch>'9') {if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
    return s*w;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
inline void print(int x)
{
    write(x);
    putchar('
');
}
inline int lowbit(int x)
{
    return x&(-x);
}
inline void update(int x,int y)
{
    for(register int i=x;i<=n;i+=lowbit(i)) a[i]+=y;
}
inline int getsum(int x)
{
    ans=0;
    for(register int i=x;i;i-=lowbit(i)) ans+=a[i];
    return ans;
}
inline void add(int l,int r,int x)
{
    update(l,x);update(r+1,-x);
}
int main()
{
    n=read();m=read();
    for(register int i=1;i<=n;++i)
    {
        now=read();
        update(i,now-last);
        last=now;
    }
    for(register int i=1;i<=m;++i)
    {
        num=read();
        if(num==1)
        {
            x=read();y=read();k=read();
            add(x,y,k);
        }
        else
        {
            x=read();
            print(getsum(x));
        }
    }
    return 0;
}

5.总结

参考资料：

https://www.cnblogs.com/xenny/p/9739600.html

https://blog.csdn.net/bestsort/article/details/80796531

https://www.luogu.com.cn/blog/kingxbz/shu-zhuang-shuo-zu-zong-ru-men-dao-ru-fen

练习：求逆序对。

#include<bits/stdc++.h>
#define int long long
using namespace std;
struct arr
{
    int sum,num;
}A[500002];
int a[500002];
int f[500002];
int n;
int x;
int ans;
inline int read()
{
    int s=0,w=1;
    char ch=getchar();
    while(ch<'0'||ch>'9') {if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
    return s*w;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
inline void print(int x)
{
    write(x);
    putchar('
');
}
inline int lowbit(int x)
{
    return x&(-x);
}
inline void update(int x,int y)
{
    for(int i=x;i<=n;i+=lowbit(i)) f[i]+=y;
}
inline int getsum(int x)
{
    int sum=0;
    for(int i=x;i;i-=lowbit(i)) sum+=f[i];
    return sum;
}
bool cmp(arr x,arr y)
{
    if(x.sum!=y.sum) return x.sum<y.sum;
    return x.num<y.num;
}
signed main()
{
    n=read();
    for(int i=1;i<=n;++i) A[i].sum=read(),A[i].num=i;
    sort(A+1,A+n+1,cmp);
    for(int i=1;i<=n;++i) a[A[i].num]=i;
    for(int i=1;i<=n;++i)
    {
        update(a[i],1);
        ans+=i-getsum(a[i]);
    }
    print(ans);
    return 0;
}