算法学习——虚树

虚树听起来是一个很高大上的东西，实际上实现起来是比较简单的。

大致的意思是说，对于一棵树而言，也许每次询问我们只需要用到其中的部分节点，因此如果每次询问我们要对全部的节点都做一次处理的话，显然会造成浪费，且很可能会超时。

这时就需要虚树了。

因为有些节点是完全无用的，但你又不能因此毁了原树——说不定下次询问还要用呢？

所以我们可以提取出需要用到的部分节点，重新建一棵树。

我们把需要用到的节点称之为关键点。

比如对于这样一张图：

 

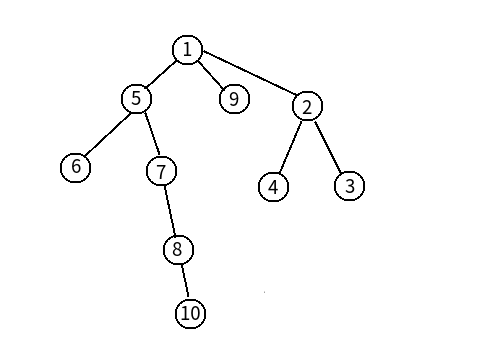
如果给定关键点是1, 6, 10， 那么建出来的虚树是这样的：

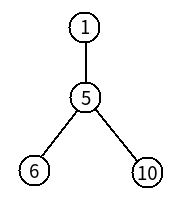
除了给定的关键点外，我们还需要加入一些其他的点作为关键点，来把各个关键点联系起来，而这些新加入的点就是相邻2点的LCA。

那么如何构建出这棵虚树呢？

如果我们按照dfn的顺序来加入节点，这样的话就跟树链剖分有点类似了。

对于这棵还没有构建出来的虚树，我们可以将其剖分成几条链，分别连接，这样的话我们就相当于加入节点的时候只需要维护一条链，而不是树。

而因为我们在树上进行DP等操作时肯定要用到点到root的路径，因此这条链应该是这个点到达root的路径。

但用重儿子来剖分显然是不行的，毕竟你都不知道重儿子会不会是关键点。但是用dfn的话既有明确的顺序，又可以保证在后面加入的点一定不会是前面的点的父亲，因此我们选用dfn。

首先我们依次加入1 6这2个点，现在它们构成了一条链。

然后加入10这个点，这时我们发现，10这个点的LCA是5，而5在1的下面，因此如果我们要得到10到root的路径，1是必须保留的，5作为LCA显然也是必须保留的。

而6对于我现在要维护的新链并没有什么用，因此我们要舍弃掉6，并连上5 ---> 6，然后把5和10依次加入栈。

这时我们发现没有新的点要加入了，于是弹出栈内所有元素，并且每弹出一个元素，就要把这个元素和上一个元素连一条边

 于是我们就建好了一棵虚树。

不过有时我们并不需要把树实实在在的建出来

因为既然我们已经可以根据一个序列建出一棵虚树了，其实也完全可以通过这个序列来遍历这棵树，而不是把它建出来再遍历。

但是这种方法适用性没有那么广。

（下面的代码是消耗战（入门题）的）

// luogu-judger-enable-o2
#include<bits/stdc++.h>
using namespace std;
#define R register int
#define AC 250010
#define ac 500100
#define LL long long

int n, m, timer, cnt, k;
int p[ac], t[ac], st[ac][20], dfn[AC], dep[AC], num[ac], first[AC];
LL f[AC], val[AC], len[ac];//error !!!这里应该是ac！！！
int d[AC], s[AC], top;
int Head[AC], date[ac], Next[ac], tot;//原树,用完可以重复利用来建虚树
    
inline int read()
{
    int x = 0;char c = getchar();
    while(c > '9' || c < '0') c = getchar();
    while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return x;
}    

inline void add1(int f, int w, LL S)
{
    date[++tot] = w, Next[tot] = Head[f], Head[f] = tot, len[tot] = S;
    date[++tot] = f, Next[tot] = Head[w], Head[w] = tot, len[tot] = S;
}

inline void add2(int f, int w)
{
    date[++tot] = w, Next[tot] = Head[f], Head[f] = tot;
    date[++tot] = f, Next[tot] = Head[w], Head[w] = tot;
    //printf("%d ---> %d
", f, w);
}

void dfs1(int x)//求出dfn和一些附带信息
{
    int now;
    dfn[x] = ++timer, num[++cnt] = x, first[x] = cnt;
    for(R i = Head[x]; i; i = Next[i])//存下第一次出现的位置
    {
        now = date[i];
        if(dfn[now]) continue;
        dep[now] = dep[x] + 1;
        val[now] = min(len[i], val[x]);//求出这个点到root这条链上的最小代价
        dfs1(now);
        num[++cnt] = x;//应该是每次到达这个节点都要计入
    }
    //num[++cnt] = x;//存下遍历序列
}

void pre()
{
    int a, b, c;
    n = read(), val[1] = 1e18;
    for(R i = 1; i < n; i ++)
    {
        a = read(), b = read(), c = read();
        add1(a, b, c);
    }
    dep[1] = 1;
    dfs1(1);
}

int Max(int x, int y)
{
    if(dep[num[x]] < dep[num[y]]) return x;
    else return y;
}

int Min(int x, int y)
{
    if(x < y) return x;
    else return y;
}

void build()//建出st表
{//查询的应该是遍历序列上的深度最小值
    for(R i = 1; i <= cnt; i ++) st[i][0] = i;
    int tmp = 1, rnt = 0;
    for(R i = 1; i <= cnt; i ++)
    {
        if(i == tmp * 2) tmp <<= 1, ++rnt;
        p[i] = tmp, t[i] = rnt;//p[i]表示小于等于i的最大的2的次幂
    }
    tmp = 1;
    for(R i = 1; i <= 19; i ++)//枚举长度
    {
        for(R j = 1; j <= cnt; j ++)
            st[j][i] = Max(st[j][i - 1], st[Min(j + tmp, cnt)][i - 1]);
        tmp <<= 1;
    }
}

int LCA(int x, int y)
{
    if(x > y) swap(x, y);
    int len = y - x + 1;
    return num[Max(st[x][t[len]], st[y - p[len] + 1][t[len]])];
}

void dfs2(int x, int fa)
{
    int now;LL tmp = 0;
    f[x] = val[x];
    for(R i = Head[x]; i; i = Next[i])
    {
        now = date[i];
        if(now == fa) continue;
        dfs2(now, x);
        tmp += f[now];
    }
    Head[x] = 0;
    if(tmp && tmp < f[x]) f[x] = tmp;
}

inline bool cmp(int a, int b)
{
    return dfn[a] < dfn[b];
}

void get()
{
    int rnt = 1;
    //memset(Head, 0, sizeof(Head));
    k = read(), tot = 0;
    for(R j = 1; j <= k; j ++) d[j] = read();
    sort(d + 1, d + k + 1, cmp);
    s[1] = top = 1;
    for(R i = 2 ; i <= k; i ++)
        if(LCA(first[d[i]], first[d[rnt]]) != d[rnt]) d[++rnt] = d[i];
    for(R i = 1; i <= rnt; i ++)
    {
        int lca = LCA(first[d[i]], first[s[top]]);
        while(1)
        {
            if(dfn[lca] > dfn[s[top - 1]])
            {
                if(lca != s[top]) add2(lca, s[top]), -- top;
                if(lca != s[top]) s[++top] = lca;//因为top已经-1了，所以这里的top是上面的top-1
                break;
            }
            add2(s[top - 1], s[top]), -- top;//否则就还要一直弹出
        }
        s[++top] = d[i];
    }    
    while(top > 1) add2(s[top - 1], s[top]), --top;
    //printf("--------------");
}

void work()
{
    m = read();
    for(R i = 1; i <= m; i ++)
    {
        get();
        dfs2(1, 0);
        printf("%lld
", f[1]);
    }
}

int main()
{
//    freopen("in.in", "r", stdin);
    pre();
    build();//构建st数组
    memset(Head, 0, sizeof(Head));
    work();
//    fclose(stdin);
    return 0;
}