正交匹配追踪(OMP)算法的MATLAB函数代码并给出单次测试例程代码
测量数M与重构成功概率关系曲线绘制例程代码
信号稀疏度K与重构成功概率关系曲线绘制例程代码
参考来源:http://blog.csdn.net/jbb0523/article/details/45130793
参考文献:Joel A. Tropp and Anna C. Gilbert. Signal Recovery From Random Measurements Via Orthogonal Matching Pursuit[J]. IEEETransactions on Information Theory, VOL. 53, NO. 12, DECEMBER 2007.
0、符号说明如下
压缩观测y=Φx,其中y为观测所得向量M×1,x为原信号N×1(M<<N)。x一般不是稀疏的,但在某个变换域Ψ是稀疏的,即x=Ψθ,其中θ为K稀疏的,即θ只有K个非零项。此时y=ΦΨθ,令A=ΦΨ,则y=Aθ。
(1)y为观测所得向量,大小为M×1
(2)x为原信号,大小为N×1
(3)θ为K稀疏的,是信号在x在某变换域的稀疏表示
(4)Φ称为观测矩阵、测量矩阵、测量基,大小为M×N
(5)Ψ称为变换矩阵、变换基、稀疏矩阵、稀疏基、正交基字典矩阵,大小为N×N
(6)A称为测度矩阵、传感矩阵、CS信息算子,大小为M×N
上式中,一般有K<<M<<N,后面三个矩阵各个文献的叫法不一,以后我将Φ称为测量矩阵、将Ψ称为稀疏矩阵、将A称为传感矩阵。
1、OMP重构算法流程



2、正交匹配追踪(OMP)MATLAB代码(CS_OMP.m)
function[theta]=CS_OMP(y,A,t)
%CS_OMP Summary of this function goes here
%Version: 1.0 written by jbb0523 @2015-04-18
% Detailed explanation goes here
% y = Phi * x
% x = Psi * theta
% y = Phi*Psi * theta
% 令 A = Phi*Psi, 则y=A*theta
% 现在已知y和A,求theta
[y_rows,y_columns]=size(y);
ify_rows<y_columns
y=y';%y should be a column vector
end
[M,N]=size(A); %传感矩阵A为M*N矩阵
theta=zeros(N,1); %用来存储恢复的theta(列向量)
At=zeros(M,t); %用来迭代过程中存储A被选择的列
Pos_theta=zeros(1,t); %用来迭代过程中存储A被选择的列序号
r_n=y; %初始化残差(residual)为y
forii=1:t %迭代t次,t为输入参数
product=A'*r_n; %传感矩阵A各列与残差的内积
[val,pos]=max(abs(product)); %找到最大内积绝对值,即与残差最相关的列
At(:,ii)=A(:,pos); %存储这一列
Pos_theta(ii)=pos; %存储这一列的序号
A(:,pos)=zeros(M,1); %清零A的这一列,其实此行可以不要,因为它与残差正交
%y=At(:,1:ii)*theta,以下求theta的最小二乘解(Least Square)
theta_ls=(At(:,1:ii)'*At(:,1:ii))^(-1)*At(:,1:ii)'*y; %最小二乘解
%At(:,1:ii)*theta_ls是y在At(:,1:ii)列空间上的正交投影
r_n=y-At(:,1:ii)*theta_ls; %更新残差
end
theta(Pos_theta)=theta_ls; %恢复出的theta
end
3、OMP单次重构测试代码(CS_Reconstuction_Test.m)
代码中,直接构造一个K稀疏的信号,所以稀疏矩阵为单位阵。
%压缩感知重构算法测试
clear all;close all;clc;
M=64;%观测值个数
N=256;%信号x的长度
K=10;%信号x的稀疏度
Index_K=randperm(N);
x=zeros(N,1);
x(Index_K(1:K))=5*randn(K,1);%x为K稀疏的,且位置是随机的
Psi=eye(N);%x本身是稀疏的,定义稀疏矩阵为单位阵x=Psi*theta
Phi=randn(M,N);%测量矩阵为高斯矩阵
A=Phi*Psi;%传感矩阵
y=Phi*x;%得到观测向量y
%% 恢复重构信号x
tic
theta=CS_OMP(y,A,K);
x_r=Psi*theta;% x=Psi * theta
toc
%% 绘图
figure;
plot(x_r,'k.-');%绘出x的恢复信号
hold on;
plot(x,'r');%绘出原信号x
hold off;
legend('Recovery','Original')
fprintf('
恢复残差:');
norm(x_r-x)%恢复残差
代码解释:上述代码是直接构造一个K稀疏的信号,接下来解释一下代码中是如何构造该稀疏信号的。
首先介绍一下randperm函数,即randm permutation随机排列、随机置换。功能是随机打乱一个数字序列,其内的参数决定了随机数的范围。
Index_K = randperm(N); 指的是将1到256的数进行随机排列
初始化信号x:x = zeros(N,1);
x(Index_K(1:K)) = 5*randn(K,1);等式右边比较好理解,即构造一个K*1的随机向量,接着解释等式左边,括号内Index_K(1:K)指的是选取随机排列后的数列的前K项,因为我们要构造的信号是K稀疏的,也就是只有K个项为非零元素。则我们要将等式右边产生的K个非零值随机的插到信号x的K个位置中,举个例子,比如经过排列后的Index_K(1:K)=12 56 30 17 5 2 6 98 200 85 ,则等式右边的K个非零值被放置在x的第12、56……的位置上。
接着解释最后一行代码,norm指的是范数的意思,在代码中求得是重构后的信号与原始信号的差值的一范数,一范数相当于求绝对值,据此求出误差。
运行结果如下:(信号为随机生成,所以每次结果均不一样)
1)图:
2)Command Windows
Elapsed time is 0.849710 seconds.
恢复残差:
ans =
5.5020e-015
4、测量数M与重构成功概率关系曲线绘制例程代码
这段代码真的是断断续续看了好久才明白,理解代码还是要分块分块搞懂
%压缩感知重构算法测试CS_Reconstuction_MtoPercentage.m
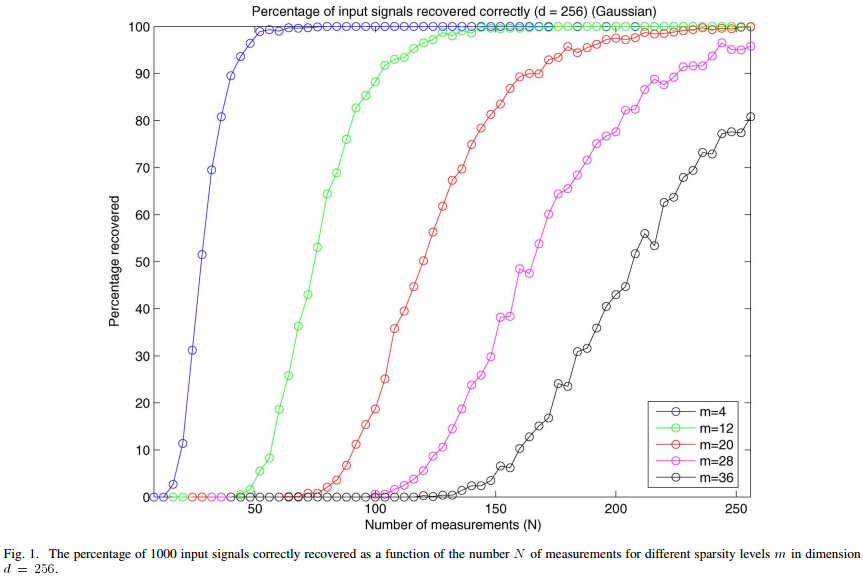
% 绘制参考文献中的Fig.1
% 参考文献:Joel A. Tropp and Anna C. Gilbert
% Signal Recovery From Random Measurements Via Orthogonal Matching
% Pursuit,IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 53, NO. 12,
% DECEMBER 2007.
% Elapsed time is 1171.606254 seconds.(@20150418night)
clear all;close all;clc;
%% 参数配置初始化
CNT=1000;%对于每组(K,M,N),重复迭代次数
N=256;%信号x的长度
Psi=eye(N);%x本身是稀疏的,定义稀疏矩阵为单位阵x=Psi*theta
K_set=[4,12,20,28,36];%信号x的稀疏度集合
Percentage=zeros(length(K_set),N);%存储恢复成功概率
%% 主循环,遍历每组(K,M,N)
tic
forkk=1:5
K=K_set(kk);%本次稀疏度
M_set=K:5:N;%M没必要全部遍历,每隔5测试一个就可以了
PercentageK=zeros(1,length(M_set));%存储此稀疏度K下不同M的恢复成功概率
formm=1:length(M_set)
M=M_set(mm);%本次观测值个数
P=0;
forcnt=1:CNT%每个观测值个数均运行CNT次
Index_K=randperm(N);
x=zeros(N,1);
x(Index_K(1:K))=5*randn(K,1);%x为K稀疏的,且位置是随机的
Phi=randn(M,N);%测量矩阵为高斯矩阵
A=Phi*Psi;%传感矩阵
y=Phi*x;%得到观测向量y
theta=CS_OMP(y,A,K);%恢复重构信号theta
x_r=Psi*theta;% x=Psi * theta
ifnorm(x_r-x)<1e-6%如果残差小于1e-6则认为恢复成功
P=P+1;
end
end
PercentageK(mm)=P/CNT*100;%计算恢复概率
end
Percentage(kk,1:length(M_set))=PercentageK;
end
toc
save MtoPercentage1000%运行一次不容易,把变量全部存储下来
%% 绘图
S=['-ks';'-ko';'-kd';'-kv';'-k*'];
figure;
forkk=1:length(K_set)
K=K_set(kk);
M_set=K:5:N;
L_Mset=length(M_set);
plot(M_set,Percentage(kk,1:L_Mset),S(kk,:));%绘出x的恢复信号
hold on;
end
hold off;
xlim([0256]);
legend('K=4','K=12','K=20','K=28','K=36');
xlabel('Number of measurements(M)');
ylabel('Percentage recovered');
title('Percentage of input signals recovered correctly(N=256)(Gaussian)');
这段代码指的是固定稀疏度的情况下,研究测量次数与重构概率的关系,突然间不知道测量次数指什么。观测矩阵大小为M*N,测量次数也就是指的这个M的大小,也就是我们压缩采样的采样点数。
8-14行代码都是初始化,但是第14行代码,Percentage = zeros(length(K_set),N);为什么维度要这样设置呢?我们要得出的图形是以测量次数M为横坐标,重构概率为纵坐标的,测量次数最大为数据的长度,也就是N,因为我们在仿真中对不同稀疏度的情况进行了仿真,共仿真5种不同稀疏度的情况,所以行数为5,即length(K_set)
接着在第17行进入了主循环,第19行M_set = K:5:N;没必要全部遍历,所以每隔5个对该点的值进行测试,但为什么要从K开始呢?K指的是信号的稀疏度,就是信号x最多的非零元素,所以我们进行观测的时候最少要观测到所有非零元素,所以从K开始。执行完这行代码之后生成一个测量次数的行向量,注意不同稀疏度下的测量次数集合是不同的。
选择了此次测试的稀疏度后,第21行代码开始对该稀疏度下的测量次数与重构精度的关系进行了测试。依次 选择测量次数集合M_set中的测量次数,第23行初始化P=0,后面如果残差小于某一个值时,即重构成功时,P+1。每个观测值重复1000次操作。
第25到32行是生成稀疏信号并进行OMP重构,得到重构后的信号。
第37行代码,重复试验1000次后,记录下当前测量次数下的恢复概率,P指的是重构成功的个数,除以1000次试验次数再乘上100即得到重构的概率。
接着进行下一个观测次数的循环。
M_set集合中的测量次数全部执行完毕后,执行第39行代码:Percentage(kk,1:length(M_set)) = PercentageK,将此次稀疏度下测得的重构概率保存到Percentage中,Percentage的行数是稀疏度的个数,列数是测量次数的个数。
第44行代码开始是绘图,根据稀疏度先得到测量次数的集合,然后以测量次数M为横轴,重构概率为纵轴绘制图形。
本程序运行结果:
文献中的Fig.1:
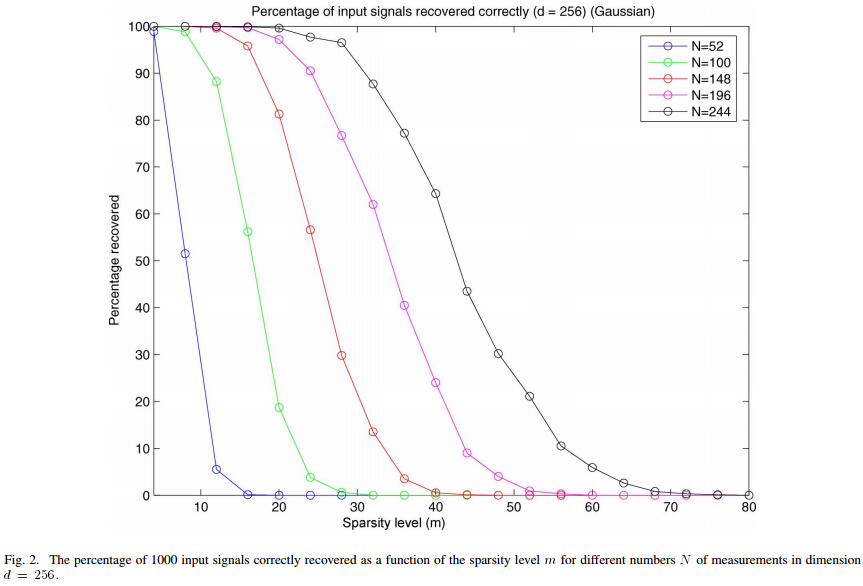
5、信号稀疏度K与重构成功概率关系曲线绘制例程代码
代码与4中的类似
%压缩感知重构算法测试CS_Reconstuction_KtoPercentage.m % 绘制参考文献中的Fig.2 % 参考文献:Joel A. Tropp and Anna C. Gilbert % Signal Recovery From Random Measurements Via Orthogonal Matching % Pursuit,IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 53, NO. 12, % DECEMBER 2007. % Elapsed time is 1448.966882 seconds.(@20150418night) clear all;close all;clc; %% 参数配置初始化 CNT=1000;%对于每组(K,M,N),重复迭代次数 N=256;%信号x的长度 Psi=eye(N);%x本身是稀疏的,定义稀疏矩阵为单位阵x=Psi*theta M_set=[52,100,148,196,244];%测量值集合 Percentage=zeros(length(M_set),N);%存储恢复成功概率 %% 主循环,遍历每组(K,M,N) tic formm=1:length(M_set) M=M_set(mm);%本次测量值个数 K_set=1:5:ceil(M/2);%信号x的稀疏度K没必要全部遍历,每隔5测试一个就可以了 PercentageM=zeros(1,length(K_set));%存储此测量值M下不同K的恢复成功概率 forkk=1:length(K_set) K=K_set(kk);%本次信号x的稀疏度K P=0; forcnt=1:CNT%每个观测值个数均运行CNT次 Index_K=randperm(N); x=zeros(N,1); x(Index_K(1:K))=5*randn(K,1);%x为K稀疏的,且位置是随机的 Phi=randn(M,N);%测量矩阵为高斯矩阵 A=Phi*Psi;%传感矩阵 y=Phi*x;%得到观测向量y theta=CS_OMP(y,A,K);%恢复重构信号theta x_r=Psi*theta;% x=Psi * theta ifnorm(x_r-x)<1e-6%如果残差小于1e-6则认为恢复成功 P=P+1; end end PercentageM(kk)=P/CNT*100;%计算恢复概率 end Percentage(mm,1:length(K_set))=PercentageM; end toc save KtoPercentage1000test%运行一次不容易,把变量全部存储下来 %% 绘图 S=['-ks';'-ko';'-kd';'-kv';'-k*']; figure; formm=1:length(M_set) M=M_set(mm); K_set=1:5:ceil(M/2); L_Kset=length(K_set); plot(K_set,Percentage(mm,1:L_Kset),S(mm,:));%绘出x的恢复信号 hold on; end hold off; xlim([0125]); legend('M=52','M=100','M=148','M=196','M=244'); xlabel('Sparsity level(K)'); ylabel('Percentage recovered'); title('Percentage of input signals recovered correctly(N=256)(Gaussian)');
本程序运行结果:
文献中的Fig.2: