PCA主成分分析
PCA降维。基于方差降维,属于无监督学习。无需数据标签。
使方差(数据离散量)最大,变换后数据分开。更易于分类。
可以对隐私数据PCA,数据加密。

基变换
投影->内积

基变换
正交的基,两个向量垂直(内积为0,线性无关)
先将基化成各维度下的单位向量。
一般把数据写成列向量的形式,新的基写成矩阵的形式。
基×向量(基要在左乘,行表示一组基向量;样本在右,列对应一个样本,m列即m个样本(n*m))

R个基向量,行向量表示。R维空间内,p1...pr。p是行向量。
m个样本,m列。n个特征。
将右面矩阵内每一个列向量(样本),映射到R维空间内

原来可能有n个特征,现在变成了R个特征。m个样本:

基的选择
选择一组基,要尽可能保留原来信息,但又更离散(方差大),易于分类。
数据预处理,标准化,使均值为0。
方差:Var(a)=1/m*{减去均值后求和}。方差表示一个特征的离散程度。
协方差:为两个值相乘。协方差(绝对值)越大表示两个特征越相关,为0则无关。

二维的数据点,投影到一维。寻找方差最大的方向。
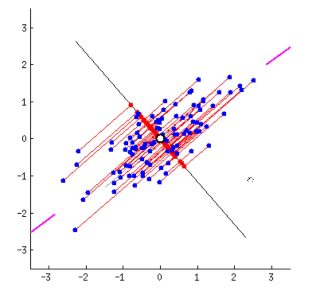


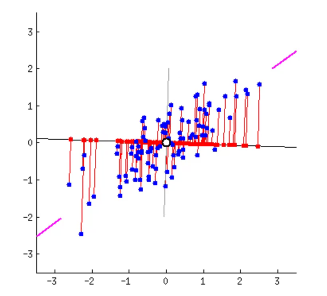
可以发现,第二个图中,刚好直线上投影点更离散。
协方差
先会对数据中心化,变成均值为0。即类似方差中的μ=0。a^2->a
m个样本


可以发现,协方差矩阵中刚好包含了所需要考虑的方差与协方差。
且二者的位置关系十分巧妙,方差恰好在主对角线上,协方差在对角。
需求可以恰好等价为协方差矩阵对角化。
即,寻找基,使得协方差矩阵对角化。


协方差矩阵同时包含了方差和协方差。
希望方差最大,协方差最小。
最大的特征值对应的特征向量,就是方差最大。选前k个最大的,k个单位向量->最好的k个基
实例

这里,求得最大的特征值后,可以直接找对应的特征向量来用,对角化步骤貌似可以省略。
二维,5个样本
降到一维,选一个c1
两个特征向量,一定是可以把协方差矩阵对角化。