使用sklearn进行数据挖掘-房价预测(3)—绘制数据的分布

使用sklearn进行数据挖掘系列文章：

• 1.使用sklearn进行数据挖掘-房价预测(1)
• 2.使用sklearn进行数据挖掘-房价预测(2)—划分测试集
• 3.使用sklearn进行数据挖掘-房价预测(3)—绘制数据的分布
• 4.使用sklearn进行数据挖掘-房价预测(4)—数据预处理
• 5.使用sklearn进行数据挖掘-房价预测(5)—训练模型
• 6.使用sklearn进行数据挖掘-房价预测(6)—模型调优

可视化数据###

目前我们只是大概了解了数据的类型，以及对数据集进行了划分，下面我们要对数据进行更深一步的探索，以下的操作只在训练集上面进行，由于该数据集比较的小，我们就直接在数据集上面进行操作，为了防止数据集被修改，我们先复制一份。

housing = strat_train_set.copy()

这个数据集提供经纬度这些地理位置信息，那么我们可以根据这些信息将数据分布绘制出来

看着像什么？你没有猜错，这就是加利福尼亚州的形状，这个图形看着有点稠密，可以通过设置alpha来设置图形的显示。

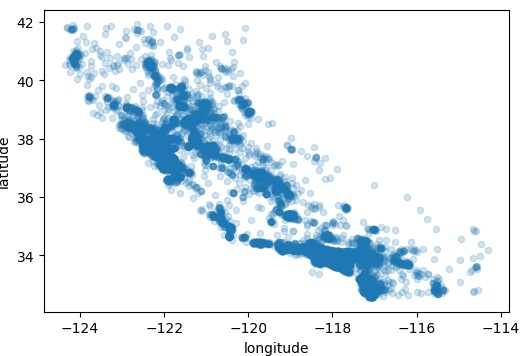
我们对图像敏感，但要发现图像中的某些规律还是需要我们调节一下参数的，现在我们就能清楚的从图中看到稠密的地区了，接下来我们将房价、人口也加入图中，

import matplotlib.pyplot as plt
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
    s=housing["population"]/100, label="population", figsize=(10,7),
    c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
    sharex=False)
plt.legend()

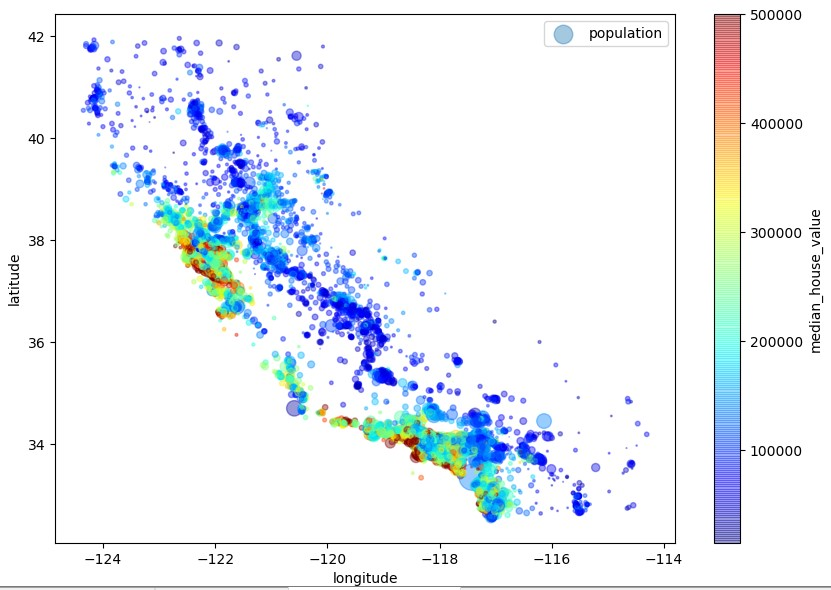
图中的小圆圈是代表该区域的人口由参数s控制，颜色代表该区域的房价由参数c控制。
从上面的图中可以得出一些规律：房价不仅与地理位置有关，还和人口稠密度有关，这些也都是一些常识。
相关性
下面我们看一看各个特征与median_house_value这一特征的相关性，使用的是皮尔逊相关系数Pearson

corr_matrix = housing.corr()
>>print corr_matrix['median_house_value'].sort_values(ascending=False)
median_house_value    1.000000
median_income         0.687160
total_rooms           0.135097
housing_median_age    0.114110
households            0.064506
total_bedrooms        0.047689
population           -0.026920
longitude            -0.047432
latitude             -0.142724
Name: median_house_value, dtype: float64

相关系数的取值范围为[-1,1]，当值趋近1时，表示特征之间具有强的正相关性，反之为负相关。值趋近于0表示特征之间不存在线性关系。值得注意的是，这里说的相关性只针对线性相关。如果为非线性关系则该衡量标准失效，如下图最后一行，它们的相关系数为0，显然他们是存在某种关系的。第二行的相关性都为1或-1说明了相关性与斜率无关。

上面是通过计算相关系数矩阵找出特征之间的相关性，还有一种方法是通过绘制特征之间分布，pandas提供了scatter_matrix方法，顾名思义就是使用散点图形式绘制出特征与特征之间的关系。取出相关系数排名前四的特征作为我们需要绘制的属性，会得到一个4*4个图像，代码如下：

from pandas.tools.plotting import scatter_matrix
attribute = ['median_house_value','median_income','total_rooms','housing_median_age']
scatter_matrix(housing[attribute],figsize=(10,6))

特征的组合###

前面介绍了通过可视化数据的方法来从发现潜在的规律，我们发现了特征之间的关系、还发现了一些特征有着长尾分布，以上发现的这些规律有助于我们对特征进行选择，或者对数据进行转化（如取log）等等，还有一个步骤我们可以尝试使用，那就是特征组合。在这里本文使用了总房间数、家庭人数以及人口数这三个特征的组合。

housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"]=housing["population"]/housing["households"]

corr_matrix = housing.corr()
print corr_matrix["median_house_value"].sort_values(ascending=False)

相关系数结果：

median_house_value          1.000000
median_income               0.687160
rooms_per_household         0.146285 //
total_rooms                 0.135097
housing_median_age          0.114110
households                  0.064506
total_bedrooms              0.047689
population_per_household   -0.021985//
population                 -0.026920
longitude                  -0.047432
latitude                   -0.142724
bedrooms_per_room          -0.259984//

从上面结果可以看出bedrooms_per_room较total_bedrooms 有着更高的相关性，bedrooms/rooms比越小的房价越高，从rooms_per_household可以看出，房子越大房价越贵。