深度学习中的激活函数

本节内容比较简单，通过python的matplotlib模块画出深度学习中常用的激活函数

import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
z = np.linspace(-5,5,200)

sigmoid###

首先是sigmoid相信大家都不陌生，大家学习逻辑回归和神经网络的时候经常遇到。

def logit(z):
    return 1 / (1 + np.exp(-z))
plt.plot([-5,5],[0,0],'k-')
plt.plot([-5,5],[1,1],'k--')
plt.plot([0, 0], [-0.2, 1.2], 'k-')
plt.plot(z, logit(z), "b-",linewidth=2)
props = dict(facecolor='black', shrink=0.1)
plt.annotate('Saturating', xytext=(3.5, 0.7), xy=(5, 1), arrowprops=props, fontsize=14, ha="center")
plt.annotate('Saturating', xytext=(-3.5, 0.3), xy=(-5, 0), arrowprops=props, fontsize=14, ha="center")
plt.annotate('Linear', xytext=(2, 0.2), xy=(0, 0.5), arrowprops=props, fontsize=14, ha="center")
plt.axis([-5, 5, -0.2, 1.2])
plt.title("Sigmoid activation function", fontsize=14)
plt.grid(True)
plt.show()

效果：

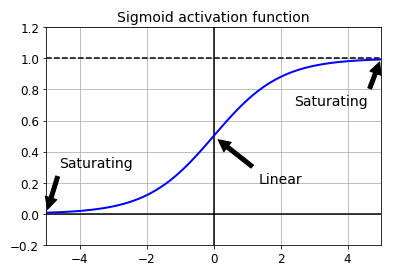
从上面的图可以看出，当输入的值比较大或者比较小的时候值会保持在0和1，常被称为saturates 。当对这些位置进行求导的时候，值接近于0。再进行BP对的时候，回传的信号会越来越弱，这种情况被称作 梯度消失(vanishing gradients)。

tanh###

plt.plot([-5,5],[0,0],'k-')#
plt.plot([-5,5],[1,1],'k--')
plt.plot([-5,5],[-1,-1],'k--')#(-5,-1),(5,-1)
plt.plot([0, 0], [-2, 2], 'k-')
plt.plot(z, np.tanh(z), "b-",linewidth=2)
plt.axis([-5, 5, -2, 2])
plt.title("Tanh activation function", fontsize=14)
plt.grid(True)
plt.show()

从图中可以看出，tanh和sigmod非常类似，只是取值范围为[-1,1]，因此tanh也面临这梯度消失的问题。

ReLU和LeakyReLU###

选择一个好的激活函数就能够很大程度上避免梯度消失问题，例如Relu,但这种方法会面临一个问题，在训练过程中部分神经元挂掉了，也就是这些神经元只会输出0，特别是当学习率比较大的时候，一旦出现这种情况，这些神经元就不会再复活。为了解决这一问题，有一种方法被提出，叫做LeakyReLU，公式很简单(LeakyReLU_a(z)=max(az,z))

def leaky_relu(z, alpha=0.01):
    return np.maximum(alpha*z, z)
plt.plot(z, leaky_relu(z, 0.05), "b-", linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([0, 0], [-0.5, 4.2], 'k-')
plt.grid(True)
props = dict(facecolor='black', shrink=0.1)
plt.annotate('Leak', xytext=(-3.5, 0.5), xy=(-5, -0.2), arrowprops=props, fontsize=14, ha="center")
plt.title("Leaky ReLU activation function", fontsize=14)
plt.axis([-5, 5, -0.5, 4.2])
plt.show()

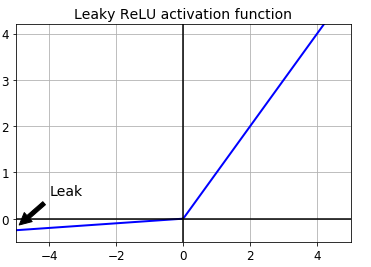
上图激活函数有一个参数(a)，控制着leaks的数量，斜率非常的小，但是能够保证神经元不会挂掉，相关研究发现，LeakyReLu的效果要优于ReLU。常用的LeakyReLU变体有

• 1.Randomized leaky ReLU(RReLU)：在训练过程中(a)是从一组选项中随机选择，在测试过程中使用它们的平均值。
• 2.Parametric leaky ReLU(PReLU):(a)是从训练集中学习得到，在较大的数据集上面效果较好，在较小的数据集上面有overfitting的风险。

ELU###

在2015年一篇名为《Fast and Accurate Deep Network Learning by Exponential Linear Units》,提出了一种新的激活函数ELU，不过和之前的ReLU相似，公式如下

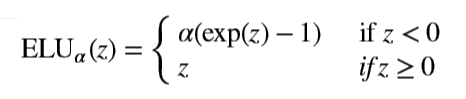
def elu(z,alpha=1):
    return np.where(z<0,alpha*(np.exp(z) - 1),z)
plt.plot(z, elu(z), "b-", linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')#(x)
plt.plot([0, 0], [-2, 5], 'k-')#(y)
plt.plot([-5,5],[-1,-1],'k--') #(虚线)
plt.show()

ELU被提出，必定存在它的优越之处：

• 1.在z<0时候 能够让神经元的输出均值接近0，(a)控制着在z<0时，激活函数的趋势，
• 2.整个函数处处可导，当z<0时，梯度的值不为0，避免了神经元挂掉的问题

SELU###

计算及技术发展日新月异，一项牛逼的技术刚出来还没火几天，就可能会有一个更牛逼的出来，下面有请scaled exponential linear units，selu，满篇幅的公式。

def selu(z,
         scale=1.0507009873554804934193349852946,
         alpha=1.6732632423543772848170429916717):
    return scale * elu(z, alpha)

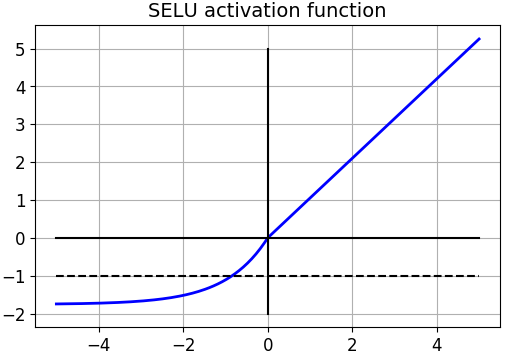
这个公式的牛逼之处在于在100层的神经网络训练过程中，能够保证均值接近0，方差为1。能够有效的避免梯度消失问题。这个激活函数和Batch Normalization目的类似，都是避免神经元的输出值发生飘移。下面模拟一个100层的网络，

np.random.seed(42)
Z = np.random.normal(size=(500, 100))#模拟的输入x
for layer in range(100):
    W = np.random.normal(size=(100, 100), scale=np.sqrt(1/100))
    Z = selu(np.dot(Z, W))
    means = np.mean(Z, axis=1)
    stds = np.std(Z, axis=1)
    if layer % 10 == 0:
        print("Layer {}: {:.2f} < mean < {:.2f}, {:.2f} < std deviation < {:.2f}".format(
            layer, means.min(), means.max(), stds.min(), stds.max()))

输出，读者可以将上面的激活函数换成其他的看一下效果

Layer 0: -0.26 < mean < 0.27, 0.74 < std deviation < 1.27
Layer 10: -0.24 < mean < 0.27, 0.74 < std deviation < 1.27
Layer 20: -0.17 < mean < 0.18, 0.74 < std deviation < 1.24
Layer 30: -0.27 < mean < 0.24, 0.78 < std deviation < 1.20
Layer 40: -0.38 < mean < 0.39, 0.74 < std deviation < 1.25
Layer 50: -0.27 < mean < 0.31, 0.73 < std deviation < 1.27
Layer 60: -0.26 < mean < 0.43, 0.74 < std deviation < 1.35
Layer 70: -0.19 < mean < 0.21, 0.75 < std deviation < 1.21
Layer 80: -0.18 < mean < 0.16, 0.72 < std deviation < 1.19
Layer 90: -0.19 < mean < 0.16, 0.75 < std deviation < 1.20

TF实现SELU的方法

def selu(z,
         scale=1.0507009873554804934193349852946,
         alpha=1.6732632423543772848170429916717):
    return scale * tf.where(z >= 0.0, z, alpha * tf.nn.elu(z))

总结###

一下子讲了这么多的激活函数，那么到底该怎么选择呢？一般来说的选择顺序为

ELU(SELU) > leaky ReLU(变体) > ReLU > tanh > logistic 

如果想要快，那就选用RELU，如果不想调节参数那就使用默认的参数(0.01 for Leaky ReLU,1 for ELU)，如果时间和计算力充足，那就RRELU或PReLU来个cross-validation。