思路
首先以那个环为框架,把所有的边连出来。如果有两条边相交,那么就把其中一条放到环外面去。
如图:

((1,3))与((2,5)相交,)(1,4)(与)(2,5)相交。所以我们把((2,5))这条边放到外面去。
就成了这样
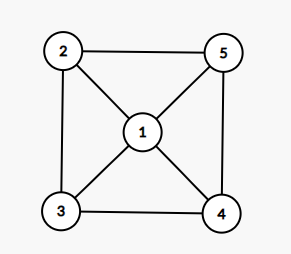
就不会有边相交了。
显然如果两条边在环内相交,那么全部挪到环外也会相交。所以只要是相交的两条边必定是一个在环内,一个在环外。
然后就是2-sat模型了。
坑点。。。
犯了一些很zz的错误。
1.如果边的数量>点的数量乘3-6,即((m > n imes 3 - 6)),可以证明必定无解。这个需要判断掉。
2. 没错,这个bug我调了很久233。。。
没错,这个bug我调了很久233。。。
4.特判的地方要放到全部数据读入之后。。。也调了很久(好zz啊啊啊)
代码
/*
* @Author: wxyww
* @Date: 2019-04-27 19:06:04
* @Last Modified time: 2019-04-27 21:28:17
*/
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<queue>
#include<vector>
#include<ctime>
using namespace std;
typedef long long ll;
const int M = 300010;
#define pi pair<int,int>
ll read() {
ll x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9') {
x=x*10+c-'0';
c=getchar();
}
return x*f;
}
struct node {
int v,nxt;
}e[M];
int head[M],ejs;
void add(int u,int v) {
e[++ejs].v = v;e[ejs].nxt = head[u];head[u] = ejs;
}
int n,m,pos[M];
pi tmp[M];
bool pd(int l,int r,int L,int R) {
if(l > r) swap(l,r);if(L > R) swap(L,R);
if((l <= L && r >= R) || (L <= l && R >= r)) return 0;
if(l >= R || L >= r) return 0;
return 1;
}
int tot,vis[M],coljs,sta[M],col[M],top,dfn[M],low[M];
void tarjan(int u) {
dfn[u] = low[u] = ++tot;
sta[++top] = u;vis[u] = 1;
for(int i = head[u];i;i = e[i].nxt) {
int v = e[i].v;
if(!dfn[v]) {
tarjan(v);
low[u] = min(low[u],low[v]);
}
else if(vis[v]) low[u] = min(low[u],low[v]);
}
if(low[u] == dfn[u]) {
++coljs;
do {
int x = sta[top--];
col[x] = coljs;
vis[x] = 0;
}while(sta[top + 1] != u);
}
}
int main() {
int T = read();
while(T--) {
memset(head,0,sizeof(head));
ejs = 0;
memset(pos,0,sizeof(pos));
coljs = 0;memset(col,0,sizeof(col));
memset(dfn,0,sizeof(dfn));memset(low,0,sizeof(low));
tot = 0;top = 0;
n = read(),m = read();
for(int i = 1;i <= m;++i) tmp[i].first = read(),tmp[i].second = read();
for(int i = 1;i <= n;++i) pos[read()] = i;
if(m > 3 * n - 6) {
puts("NO");continue;
}
for(int i = 1;i <= m;++i)
for(int j = i + 1;j <= m;++j)
if(pd(pos[tmp[i].first],pos[tmp[i].second],pos[tmp[j].first],pos[tmp[j].second]))
add(i,j + m),add(i + m,j),add(j,i + m),add(j + m,i);
for(int i = 1;i <= m + m;++i) if(!dfn[i]) tarjan(i);
int bz = 0;
for(int i = 1;i <= m;++i) if(col[i] == col[i + m]) bz = 1;
if(bz) puts("NO");else puts("YES");
}
return 0;
}