南京网络赛B-The writing on the wall

•  30.43%
•  2000ms
•  262144K

Feeling hungry, a cute hamster decides to order some take-away food (like fried chicken for only 3030 Yuan).

However, his owner CXY thinks that take-away food is unhealthy and expensive. So she demands her hamster to fulfill a mission before ordering the take-away food. Then she brings the hamster to a wall.

The wall is covered by square ceramic tiles, which can be regarded as a n * mn∗m grid. CXY wants her hamster to calculate the number of rectangles composed of these tiles.

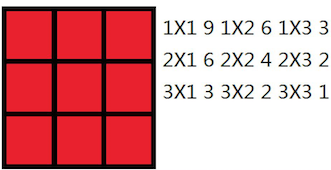
For example, the following 3 * 33∗3 wall contains 3636 rectangles:

Such problem is quite easy for little hamster to solve, and he quickly manages to get the answer.

Seeing this, the evil girl CXY picks up a brush and paint some tiles into black, claiming that only those rectangles which don't contain any black tiles are valid and the poor hamster should only calculate the number of the valid rectangles. Now the hamster feels the problem is too difficult for him to solve, so he decides to turn to your help. Please help this little hamster solve the problem so that he can enjoy his favorite fried chicken.

Input

There are multiple test cases in the input data.

The first line contains a integer TT : number of test cases. T le 5T≤5.

For each test case, the first line contains 33 integers n , m , kn,m,k , denoting that the wall is a n imes mn×m grid, and the number of the black tiles is kk.

For the next kk lines, each line contains 22 integers: x yx y ,denoting a black tile is on the xx-th row and yy-th column. It's guaranteed that all the positions of the black tiles are distinct.

For all the test cases,

1 le n le 10^5,1le m le 1001≤n≤105,1≤m≤100,

0 le k le 10^5 , 1 le x le n, 1 le y le m0≤k≤105,1≤x≤n,1≤y≤m.

It's guaranteed that at most 22 test cases satisfy that n ge 20000n≥20000.

Output

For each test case, print "Case #xx: ansans" (without quotes) in a single line, where xx is the test case number and ansans is the answer for this test case.

Hint

The second test case looks as follows:

样例输入复制

2
3 3 0
3 3 1
2 2

样例输出复制

Case #1: 36
Case #2: 20

题目来源

ACM-ICPC 2018 南京赛区网络预赛

感觉这道题和暑假牛客网多校赛有道题很像 求数独子矩阵的 按那个方法敲了

T了 本来先用vector存的 然后排序 觉得这里可能会T 改成了优先队列

但是还是T了 可能有时候logn还是比较大吧 题解的算法是nmm 和 nmlogn比可能还是会小一点

实际上题解的方式和牛客网上这道题的思路是一样的 只不过少了处理相同字母这一部分 要更简单一点

AC代码：

相当于每次从一个矩阵的最右下角开始加一个一列的矩阵，加一个两列的矩阵，加一个三列的矩阵...........

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<stack>
#include<queue>
#include<map>
#include<vector>
#include<set>
//#include<bits/stdc++.h>
#define inf 0x7f7f7f7f7f7f7f7f
using namespace std;
typedef long long LL;

const int maxn = 1e5 + 10;

int t, n, m, k;
int up[110], wall[maxn][110];


void init()
{
    memset(wall, 0, sizeof(wall));
    memset(up, 0, sizeof(up));
}

int main()
{
    cin>>t;
    for(int cas = 1; cas <= t; cas++){
        scanf("%d%d%d", &n, &m, &k);
        init();
        for(int i = 0; i < k; i++){
            int x, y;
            scanf("%d%d", &x, &y);
            wall[x][y] = 1;
        }

        LL ans = 0;
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= m; j++){
                if(wall[i][j]){
                    up[j] = i;
                }
            }

            for(int j = 1; j <= m; j++){
                LL minn = inf;
                for(int k = j; k > 0; k--){
                    minn = min(minn, (LL)(i - up[k]));
                    ans += minn;
                }
            }
        }

        printf("Case #%d: %lld
", cas, ans);
    }
	return 0;
}

TLE代码： 

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<stack>
#include<queue>
#include<map>
#include<vector>
#include<set>
//#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long LL;

const int maxn = 1e5;

int t, n, m, k;
int len[maxn], L[maxn][105], U[maxn][105];
//vector <LL> blackcol[105], blackrow[maxn];
priority_queue <int, vector<int>, greater<int> > blackcol[105], blackrow[maxn];

void init()
{
    for(int i = 1; i <= n; i++){
        while(!blackrow[i].empty()){
            blackrow[i].pop();
        }
        blackrow[i].push(0);
        //blackrow[i].clear();
        //blackrow[i].push_back(0);
    }
    for(int i = 1; i <= m; i++){
        while(!blackcol[i].empty()){
            blackcol[i].pop();
        }
        blackcol[i].push(0);
        //blackcol[i].clear();
        //blackcol[i].push_back(0);
    }
    memset(L, 0, sizeof(L));
    memset(U, 0, sizeof(U));
}

int main()
{
    cin>>t;
    for(int cas = 1; cas <= t; cas++){
        scanf("%d%d%d", &n, &m, &k);
        init();
        for(int i = 0; i < k; i++){
            int x, y;
            scanf("%d%d", &x, &y);
            blackcol[y].push(x);
            blackrow[x].push(y);
            //blackcol[y].push_back(x);
            //blackrow[x].push_back(y);
        }


        /*for(int i = 1; i <= n; i++){
            sort(blackrow[i].begin(), blackrow[i].end());
        }
        for(int i = 1; i <= m; i++){
            sort(blackcol[i].begin(), blackcol[i].end());
        }*/

        for(int i = 1; i <= n; i++){
            int now = blackrow[i].top();
            blackrow[i].pop();
            for(int j = 1; j <= m; j++){
                if(!blackrow[i].empty()){
                    if(j == blackrow[i].top()){
                        now = blackrow[i].top();
                        blackrow[i].pop();
                    }
                }
                L[i][j] = min(L[i][j - 1] + 1, j - now);

            }
        }
        for(int j = 1; j <= m; j++){
            int now = blackcol[j].top();
            blackcol[j].pop();
            for(int i = 1; i <= n; i++){
                if(!blackcol[j].empty()){
                    if(i == blackcol[j].top()){
                        now = blackcol[j].top();
                        blackcol[j].pop();
                    }
                }
                U[i][j] = min(U[i - 1][j] + 1, i - now);
            }
        }

        LL ans = 0;
        for(int j = 1; j <= m; j++){
            memset(len, 0, sizeof(len));
            for(int i = 1; i <= n; i++){
                for(int k = 0; k < L[i][j]; k++){
                    len[k] = min(len[k] + 1, U[i][j - k]);
                    if(k)len[k] = min(len[k], len[k - 1]);
                    ans += len[k];
                }
                for(int k = L[i][j]; k < m; k++)len[k] = 0;
            }
        }


        printf("Case #%d: %lld
", cas, ans);
    }
	return 0;
}