简单的图论问题【湖南省赛】

• [E] 简单的图论问题?

• 时间限制: 5000 ms　内存限制: 65535 K
• 问题描述

•  

   

   

  给一个 n 行 m 列的迷宫,每个格子要么是障碍物要么是空地。每个空地里都有一个权值。你的 任务是从找一条(r1,c1)到(r2,c2)的路径,使得经过的空地的权值之和最小。每一步可以往上下 左右四个方向之一移动一格,但不能斜着移动,也不能移动到迷宫外面或者进入障碍物格子。

  如下图,灰色格子代表障碍物。路径 A->B->D->F->E 的权值为 10+3+6+14+8=41,它是从 A 到 E 的最优路径。注意,如果同一个格子被经过两次,则权值也要加两次。

  
  

   

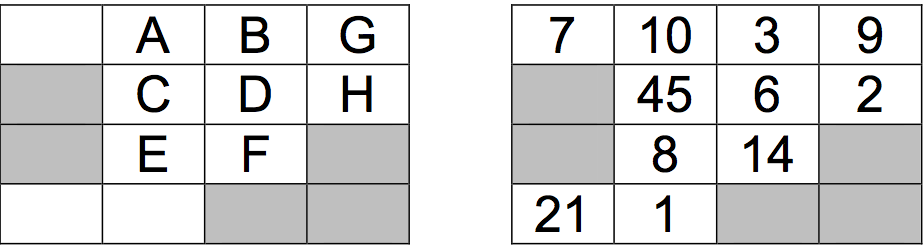
  为了让题目更有趣(顺便增加一下难度),你还需要回答另外一个问题:如果你每次必须转弯 (左转、右转或者后退,只要不是沿着上次的方向继续走即可),最小权值是多少?比如,在 上图中,如果你刚刚从 A 走到 B,那么下一步你可以走到 D 或者 A,但不能走到 G。在上图 中,A 到 E 的最优路径是 A->B->D->H->D->F->E,权和为 10+3+6+2+6+14+8=49。注意,D 经 过了两次。

  
  

   

   

   

   

• 输入
• 输入包含不超过 10 组数据。每组数据第一行包含 6 个整数 n, m, r1, c1, r2, c2 (2<=n,m<=500, 1<=r1,r2<=n, 1<=c1,c2<=m). 接下来的 n 行每行包含 m 个格子的描述。每个格子要么是一个 1~100 的整数,要么是星号"*"(表示障碍物)。起点和终点保证不是障碍物。
• 输出
• 对于每组数据,输出两个整数。第一个整数是“正常问题”的答案,第二个整数是“有趣问 题”的答案。如果每个问题的答案是“无解”,对应的答案应输出-1。
• 样例输入

• 4 4 1 2 3 2
  7 10 3 9

  * 45 6 2

  * 8 14 *
  
21 1 * * 
  2 4 1 1 1 4
  1 2 3 4
  9 * * 9
  2 4 1 1 1 4
  1 * 3 4
  9 9 * 9 

• 样例输出

• Case 1: 41 49
  Case 2: 10 -1
  Case 3: -1 -1

• 提示

• 无

• 来源

• 第十一届“蓝狐网络杯”湖南省大学生计算机程序设计竞赛

感觉这一套湖南省赛题目出的奇奇怪怪的 体验极差 好多数据类型范围什么的都要靠自己猜

还有这一题的输入也是奇奇怪怪的

emmmm搜索都不会写了 尴尬 最短路练完去练搜索好了

处理输入时候用到的一个函数 atoi 把字符串转换为整型的数

bfs 用优先队列维护 但是要改变一下排序

搜索关键要记得标记

虽然题目上说可以走回来？但是显然走回头路肯定不是正确答案

至于第二种什么有趣问题要转弯的话 就需要标记一下这个点这个方向 总之就是不能完全一样的状态重复

 

代码：

#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<map>
#include<cstring>
#include<queue>
#include<stack>
#define inf 0x3f3f3f3f

using namespace std;

int n, m, r1, c1, r2, c2;
int graph[505][505];
bool vis1[505][505], vis2[505][505][4];
int movi[4] = {-1, 0, 1, 0}, movj[4] = {0, 1, 0, -1};
struct node{
    int x, y, sum;
    int dir;
    bool friend operator < (node a, node b){
        return a.sum > b.sum;
    }
};

bool ok(int x, int y)
{
    if(x < 1 || x > n || y < 1 || y > m)
        return false;
    return graph[x][y] != 0;
}

int bfs1()
{
    priority_queue<node> q;
    node now, nextt;
    now.x = r1;
    now.y = c1;
    now.sum = graph[r1][c1];
    q.push(now);
    memset(vis1, false, sizeof(vis1));
    vis1[r1][c1] = true;
    while(!q.empty()){
        now = q.top();q.pop();
        if(now.x == r2 && now.y == c2){
            return now.sum;
        }
        for(int i = 0; i < 4; i++){
            nextt.x = now.x + movi[i];
            nextt.y = now.y + movj[i];
            if(ok(nextt.x, nextt.y) && !vis1[nextt.x][nextt.y]){
                vis1[nextt.x][nextt.y] = true;
                nextt.sum = now.sum + graph[nextt.x][nextt.y];
                q.push(nextt);
            }
        }
    }
    return -1;
}

int bfs2()
{
    priority_queue<node>q;
    node now, nextt;
    now.x = r1;
    now.y = c1;
    now.sum = graph[r1][c1];
    now.dir = -1;
    q.push(now);
    memset(vis2, false, sizeof(vis2));

    vis2[r1][c1][0] = true;
    vis2[r1][c1][1] = true;
    vis2[r1][c1][2] = true;
    vis2[r1][c1][3] = true;

    while(!q.empty()){
        now = q.top();q.pop();
        if(now.x == r2 && now.y == c2){
            return now.sum;
        }
        for(int i = 0; i < 4; i++){
            nextt.x = now.x + movi[i];
            nextt.y = now.y + movj[i];
            if(now.dir == i)
                continue;
            if(ok(nextt.x, nextt.y) && !vis2[nextt.x][nextt.y][i]){
                vis2[nextt.x][nextt.y][i] = true;
                nextt.sum = now.sum + graph[nextt.x][nextt.y];
                nextt.dir = i;
                q.push(nextt);
            }
        }
    }
    return -1;
}

int main()
{
    int cas = 1;
    while(cin>>n>>m>>r1>>c1>>r2>>c2){
        char ch[10];
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= m; j++){
                scanf("%s", ch);
                if(!strcmp(ch, "*"))
                    graph[i][j] = 0;
                else
                    graph[i][j] = atoi(ch);
                /*cin>>graph[i][j];
                if(cin.fail()){
                    graph[i][j] = 0;
                    cin.clear();
                }
                getchar();*/
            }
        }
        printf("Case %d: ", cas++);
        cout<< bfs1()<<" ";
        cout<<bfs2()<<endl;
        //getchar();

    }

    return 0;
}

emmm看到还能用dijkstra写的 其实不就是bfs嘛

不知道为什么都没有人用dfs写的