后缀树:
字符串匹配算法一般都分为两个步骤,一预处理,二匹配。
KMP和AC自动机都是对模式串进行预处理,后缀树和后缀数组则是对文本串进行预处理。
后缀树的性质:
- 存储所有 n(n-1)/2 个后缀需要 O(n) 的空间,n 为的文本(Text)的长度;
- 构建后缀树需要 O(dn) 的时间,d 为字符集的长度(alphabet);
- 对模式(Pattern)的查询需要 O(dm) 时间,m 为 Pattern 的长度;
介绍后缀树之前,我们首先要知道压缩字典树的概念。
我们在对关键字建立字典树的时候,有时某些节点只会有一个子树,没有别的支路。那么这个节点和他的子树就可以压缩成一个节点。
比如,下面是集合 {bear, bell, bid, bull, buy, sell, stock, stop} 所构建的 Trie 树。

他对应的压缩字典树就是这样的。

而后缀树就是一棵以所有的后缀为关键字建立的压缩字典树。
比如,对于文本 "banana�",其中 "�" 作为文本结束符号。下面是该文本所对应的所有后缀。
banana� anana� nana� ana� na� a� �
将每个后缀作为一个关键词,构建一棵 Trie。

然后,将独立的节点合并,形成 Compressed Trie。

则上面这棵树就是文本 "banana�" 所对应的后缀树。
像上面建立的其实是一棵显式后缀树,因为如果我们不在后缀后面加上�.某些后缀比如a,na在其他后缀的前缀中出现过,他们会被表示在一条路径上,这样的后缀树被称为隐式后缀树。
在后缀后加入一个后缀中没有出现过的字符,如�或是$可以保证后缀的唯一性,此时建立的就是一种显式后缀树。
后缀树 与 字典树 的不同在于,边(Edge)不再只代表单个字符,而是通过一对整数 [from, to] 来表示。其中 from 和 to 所指向的是 Text 中的位置,这样每个边可以表示任意的长度,而且仅需两个指针,耗费 O(1) 的空间。
后缀数组:
后缀树的建立相当的麻烦,后缀数组的提出就是为了代替后缀树,并且后缀数组节省了空间。因此题目中我们大多实现后缀数组。
其与后缀树的的关系有:
- 后缀数组可以通过对后缀树做深度优先遍历(DFT: Depth First Traversal)来进行构建,对所有的边(Edge)做字典序(Lexicographical Order)遍历。
- 通过使用后缀集合和最长公共前缀数组(LCP Array: Longest Common Prefix Array)来构建后缀树,可在 O(n) 时间内完成,例如使用 Ukkonen 算法。构造后缀数组同样也可以在 O(n) 时间内完成。
- 每个通过后缀树解决的问题,都可以通过组合使用后缀数组和额外的信息(例如:LCP Array)来解决。
后缀数组就是将文本串的所有后缀按照字典序进行排序,将后缀的起始字符的下标存入SA数组中。
比如字符串“ababa”, 他的后缀有ababa, baba, aba, ba, a
按照字典序排序为,a, aba, ababa, ba, baba他们的开始字符的下标分别为,5, 3, 1, 4, 2。因此SA[1~5]分别为5,3,1,4,2
同时我们可以用rank来记后缀在所有后缀里的排名
构建SA[i]数组中相邻元素的最长公共前缀(LCP,Longest Common Prefix),Height[i]表示SA[i]和SA[i-1]的LCP(i, j);H[i]=Height[Rank[i]表示Suffix[i]和字典排序在它前一名的后缀子串的LCP大小;
对于正整数i和j而言,最长公共前缀的定义如下: LCP(i, j) =lcp(Suffix(SA[i]), Suffix(SA[j])) = min(Height[k] | i + 1 <= k <= j)
也就是计算LCP(i, j)等同于查找Height数组中下标在i+1到j之间的元素最小值
暴力的构建后缀数组的方法复杂度是O(n^2logn),倍增算法(Doubling Algorithm)快速构造后缀数组,其利用了后缀子串之间的联系可将时间复杂度降至O(MlogN),M为模式串的长度,N为目标串的长度;另外基数排序算法的时间复杂度为O(N);Difference Cover mod 3(DC3)算法(Linear Work Suffix Array Construction)可在O(3N)时间内构建后缀数组;Ukkonen算法(On-line Construction of Suffix-Trees)可在O(N)的时间内构建一棵后缀树,然后再O(N)的时间内将后缀树转换为后缀数组,理论上最快的后缀数组构造法;
倍增法构造后缀数组,使用基数排序。基数排序在后缀数组中可以在O(n)的时间内对一个二元组(p,q)进行排序,其中p是第一关键字,q是第二关键字
我们把每个后缀分开来看。
开始时,每个后缀的第一个字母的大小是能确定的,也就是他本身的ASCLL值
具体点?把第ii个字母看做是(s[i],i)的二元组,对其进行基数排序
这样我们就得到了他们的在完成第一个字母的排序之后的相对位置关系
sa[i]:排名为i的后缀的位置
rak[i]:从第i个位置开始的后缀的排名,下文为了叙述方便,把从第i个位置开始的后缀简称为后缀i
tp[i]:基数排序的第二关键字,意义与sa一样
tax[i]:i号元素出现了多少次。辅助基数排序
s[i]:字符串
“倍增法”,每次将排序长度*2,最多需要log(n)次便可以完成排序
因此我们现在需要对每个后缀的前两个字母进行排序
此时第一个字母的相对关系我们已经知道了。
由于第i个后缀的第二个字母,实际是第i+1个后缀的第一个字母
因此每个后缀的第二个后缀的字母的相对位置关系我们也是知道的。
我们用tp这个数组把他记录出来,对rak,tp这个二元组进行基数排序
接下来我们需要对每个后缀的前四个后缀进行排序
此时我们已经知道了每个后缀前两个字母的排名,而第i个后缀的第3,4个字母恰好是第i+2个后缀的前两个字母。
他们的相对位置我们又知道啦。
这样不断排下去,最后就可以完成排序啦
举个栗子,banana先按第一个字母排序
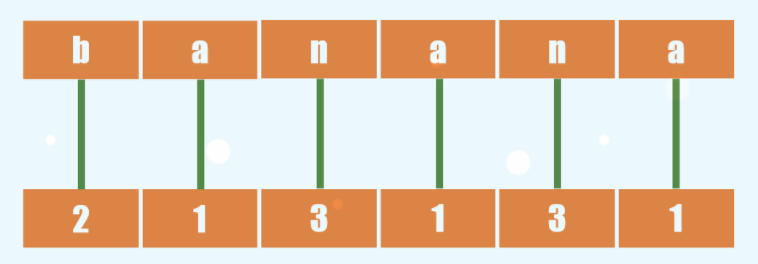
然后给前两个字母排序,也就是把相邻二元组合并。再根据字典序排

再排前四个

最长公共前缀(LCP)
对两个字符串u,v 定义函数lcp(u,v)=max{i|u=iv},对正整数i,j 定义LCP(i,j)=lcp(Suffix(SA[i]),Suffix(SA[j]),其中i,j 均为1 至n 的整数。
LCP(i,j)也就是后缀数组中第i 个和第j 个后缀的最长公共前缀的长度。
关于LCP 有两个显而易见的性质:
性质2.1 LCP(i,j)=LCP(j,i)
性质2.2 LCP(i,i)=len(Suffix(SA[i]))=n-SA[i]+1
这两个性质的用处在于,我们计算LCP(i,j)时只需要考虑i<j 的情况,因为i>j时可交换i,j,i=j时可以直接输出结果n-SA[i]+1。
并且LCP有一些定理【证明见OI2004国家集训队论文《后缀数组》许智磊,链接附在文后】
Lemma: 对任意1≤i<j<k≤n,LCP(i,k)=min{LCP(i,j),LCP(j,k)}
LCP Theorem: LCP(i,j)=min{LCP(k-1,k)|i+1≤k≤j}
LCP Corollary 对 i≤j<k,LCP(j,k)≥LCP(i,k)
定义数组height,height[i] = LCP(i-1, i),那么根据定理可得LCP(i,j)=min{height[k]|i+1≤k≤j}
那么求LCP的问题就可以变成经典的RMQ问题【如果height是固定的】,可以用线段树来维护。
【论文中提到的RMQ标准算法,O(n)时间预处理,O(1)完成查询,太菜,不会。】
设i<n,j<n,Suffix(i)和Suffix(j)满足lcp(Suffix(i),Suffix(j)>1,则成立以下两点:
Fact 1 Suffix(i)<Suffix(j) 等价于Suffix(i+1)<Suffix(j+1)。
Fact 2 一定有lcp(Suffix(i+1),Suffix(j+1))=lcp(Suffix(i),Suffix(j))-1。
那么如何高效的求height数组?
为了描述方便,设h[i]=height[Rank[i]],即height[i]=h[SA[i]]。
h 数组满足一个性质:对于i>1 且Rank[i]>1,一定有h[i]≥h[i-1]-1。
根据这个性质,可以令i从1 循环到n按照如下方法依次算出h[i]:
若 Rank[i]=1,则h[i]=0。字符比较次数为0。
若 i=1 或者h[i-1]≤1,则直接将Suffix(i)和Suffix(Rank[i]-1)从第一个字符开始依次比较直到有字符不相同,由此计算出h[i]。字符比较次数为h[i]+1,不超过h[i]-h[i-1]+2。
否则,说明i>1,Rank[i]>1,h[i-1]>1,根据性质3,Suffix(i)和Suffix(Rank[i]-1)至少有前h[i-1]-1 个字符是相同的,于是字符比较可以从h[i-1]开始,直到某个字符不相同,由此计算出h[i]。字符比较次数为h[i]-h[i-1]+2。
求出了h 数组,根据关系式height[i]=h[SA[i]]可以在O(n)时间内求出height数组,于是可以在O(n)时间内求出height 数组。
kuangbin的模板
1 /* 2 *suffix array 3 *倍增算法 O(n*logn) 4 *待排序数组长度为n,放在0~n-1中,在最后面补一个0 5 *build_sa( ,n+1, );//注意是n+1; 6 *getHeight(,n); 7 *例如: 8 *n = 8; 9 *num[] = { 1, 1, 2, 1, 1, 1, 1, 2, $ };注意num最后一位为0,其他大于0 10 *rank[] = { 4, 6, 8, 1, 2, 3, 5, 7, 0 };rank[0~n-1]为有效值,rank[n]必定为0无效值 11 *sa[] = { 8, 3, 4, 5, 0, 6, 1, 7, 2 };sa[1~n]为有效值,sa[0]必定为n是无效值 12 *height[]= { 0, 0, 3, 2, 3, 1, 2, 0, 1 };height[2~n]为有效值 13 * 14 */ 15 16 int sa[MAXN];//SA数组,表示将S的n个后缀从小到大排序后把排好序的 17 //的后缀的开头位置顺次放入SA中 18 int t1[MAXN],t2[MAXN],c[MAXN];//求SA数组需要的中间变量,不需要赋值 19 int rank[MAXN],height[MAXN]; 20 //待排序的字符串放在s数组中,从s[0]到s[n-1],长度为n,且最大值小于m, 21 //除s[n-1]外的所有s[i]都大于0,r[n-1]=0 22 //函数结束以后结果放在sa数组中 23 void build_sa(int s[],int n,int m) 24 { 25 int i,j,p,*x=t1,*y=t2; 26 //第一轮基数排序,如果s的最大值很大,可改为快速排序 27 for(i=0;i<m;i++)c[i]=0; 28 for(i=0;i<n;i++)c[x[i]=s[i]]++; 29 for(i=1;i<m;i++)c[i]+=c[i-1]; 30 for(i=n-1;i>=0;i--)sa[--c[x[i]]]=i; 31 for(j=1;j<=n;j<<=1) 32 { 33 p=0; 34 //直接利用sa数组排序第二关键字 35 for(i=n-j;i<n;i++)y[p++]=i;//后面的j个数第二关键字为空的最小 36 for(i=0;i<n;i++)if(sa[i]>=j)y[p++]=sa[i]-j; 37 //这样数组y保存的就是按照第二关键字排序的结果 38 //基数排序第一关键字 39 for(i=0;i<m;i++)c[i]=0; 40 for(i=0;i<n;i++)c[x[y[i]]]++; 41 for(i=1;i<m;i++)c[i]+=c[i-1]; 42 for(i=n-1;i>=0;i--)sa[--c[x[y[i]]]]=y[i]; 43 //根据sa和x数组计算新的x数组 44 swap(x,y); 45 p=1;x[sa[0]]=0; 46 for(i=1;i<n;i++) 47 x[sa[i]]=y[sa[i-1]]==y[sa[i]] && y[sa[i-1]+j]==y[sa[i]+j]?p-1:p++; 48 if(p>=n)break; 49 m=p;//下次基数排序的最大值 50 } 51 } 52 void getHeight(int s[],int n) 53 { 54 int i,j,k=0; 55 for(i=0;i<=n;i++)rank[sa[i]]=i; 56 for(i=0;i<n;i++) 57 { 58 if(k)k--; 59 j=sa[rank[i]-1]; 60 while(s[i+k]==s[j+k])k++; 61 height[rank[i]]=k; 62 } 63 }
参考链接:
后缀树 https://www.cnblogs.com/gaochundong/p/suffix_tree.html
后缀数组 https://www.cnblogs.com/gaochundong/p/suffix_array.html
https://www.douban.com/note/210945706/
https://www.cnblogs.com/jinkun113/p/4743694.html
OI2004国家集训队论文《后缀数组》许智磊https://github.com/Booooooooooo/OI-Public-Library/blob/master/%E5%9B%BD%E5%AE%B6%E9%9B%86%E8%AE%AD%E9%98%9F%E8%AE%BA%E6%96%871999-2017/2004/%E8%AE%B8%E6%99%BA%E7%A3%8A.pdf
OI2009国家集训队论文《后缀数组——处理字符串的有力工具》https://github.com/Booooooooooo/OI-Public-Library/blob/master/%E5%9B%BD%E5%AE%B6%E9%9B%86%E8%AE%AD%E9%98%9F%E8%AE%BA%E6%96%871999-2017/2009/%E7%BD%97%E7%A9%97%E9%AA%9E/%E5%90%8E%E7%BC%80%E6%95%B0%E7%BB%84%E2%80%94%E2%80%94%E5%A4%84%E7%90%86%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E6%9C%89%E5%8A%9B%E5%B7%A5%E5%85%B7.pdf