每天两题01

　　又是两个月的时间过去了，上一次写博客是7月14号，时间还是过的很快的，那么问题来了，为什么这么长时间都没有写东西了呢？难道是在打酱油？

　　哈哈，说起来很惭愧，刚刚开始工作，碰到各种的问题要去学习要去解决，然后业余的时间又去学了一些奇奇怪怪的东西，导致博客一直都落下了，归根到底，还是自己懒惰了，因为心中总觉得今天又工作了一天，下班了要好好放松一下。不自觉的用这种心理在安慰自己，使得自己越来越放松了，然后又因为自己有点拖延症，想要写点东西就一直拖着。。。

　　╮(￣▽￣")╭哎，话不多说了，最近源码什么的看的多了总觉得自己基础还是不够扎实，就想着业余打打基础，上班时间再看看框架写写业务逻辑什么的应该比较好，每天打基础的东西不多，就两个题，贪多嚼不烂，题目选自剑指offer，有兴趣的可以在github中自己看看哦，链接：https://github.com/CyC2018/CS-Notes

第一题：斐波那契数列

　　题目描述：大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项。 n<=39

　　

　　我的思路：什么是斐波那契数列应该还是知道一点的，公式如上图所示；简单的来说就是从第三个数开始，任意一个数等于前面两个数之和，比如0,1,1,2,3,5,8,13,22.......那么最简单的思路就是用递归，看下面代码：

public class Study01 {

    public static int feibo(int n){
        //要有下面这两个if，记住递归的话要有出口，然后会有死循环
        if (n==0) {
            return 0;
        }
        if (n==1 || n==2) {
            return 1;
        }
        return feibo(n-1)+feibo(n-2);
    }
    
    public static void main(String[] args) {
        
        int res = feibo(6);
        System.out.println(res);//8

    }
}

 　　上面的代码写出来了，但是可不可以优化一下，因为递归会导致一些值重复的计算，例如计算feibo（5）=feibo（4）+feibo（3）=[ feibo（3）+ feibo（2）]  + feibo（3）,然后这里计算机会计算两次feibo（3），这里计算机可不会像人一样合并同类项然后计算啊，而一旦计算feibo（n），当n的值很大的时候，在递归计算过程中就会有很多的这种重复计算的数，那么我们有没有办法将这种重复计算的数给剔除呢？只计算一次然后存起来，下一次再计算的话直接去拿就好了；

　　

　　改进1：新建一个数组，我们从n=0开始，将每次算出来的数放到数组中，那么数组中第n个位置的数就是我们需要的结果

//改进方式1
    public static int feiboUp01(int n){
        if (n==0) {
            return 0;
        }
        if (n==1 || n==2) {
            return 1;
        }
        int[] arr = new int[n+1];
        arr[0]=0;
        arr[1]=1;
        arr[2]=1;
        //这个循环每一次都会就算出来一个值填充到数组中，直到算出arr[n]
        for (int i = 3; i <= n; i++) {
            arr[i]=arr[i-1]+arr[i-2];
        }
        return arr[n];
    }
    
    public static void main(String[] args) {
        
        int res = feiboUp01(6);
        System.out.println(res);//8

    }

　　

　　改进二：不知道有没有发现上面这种做法虽然巧妙的利用了数组，但是对于我们来说，除了数组中的最后一个数，其他的数都是没有什么必要的，难道计算一个非常大的n，就要new一个这么大的数组吗？所以我们还可以继续改进一下；

//改进方式2
    public static int feiboUp02(int n){
        if (n==0) {
            return 0;
        }
        if (n==1 || n==2) {
            return 1;
        }
        //这里的三个变量，比如0,1,1,2,3,5，当current为5的时候，pre就是3，prepre就是2
        int prepre=1;
        int pre=1;
        int current = 0;
        //这里有点不好理解，三个数prepre    pre    current
        //经过一次循环，计算current = prepre+pre，这个时候也要将prepre和pre往右移动一个位置，将
        //原来的pre指向现在的current，原来的prepre指向现在的pre
        for (int i = 3; i <= n; i++) {
            current = prepre+pre;
            prepre = pre;
            pre = current;
        }
        return current;
    }
    public static void main(String[] args) {
        
        int res = feiboUp02(6);
        System.out.println(res);

    }

 第二题：我们可以用 2x1 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 2x1 的小矩形无重叠地覆盖一个 2xn 的大矩形，总共有多少种方法？

　　这个问题其实还是斐波那契数列，但是思路很有趣，一般我们想办法计算有多少种方法的时候，可能就去画图计算去了，但是这里却是将一个大的问题拆成子问题，而子问题可以继续拆...

　　如果n=1，只有一种情况，

　　如果n=2，只有两种，两块都横着或者两块都竖着

 　　

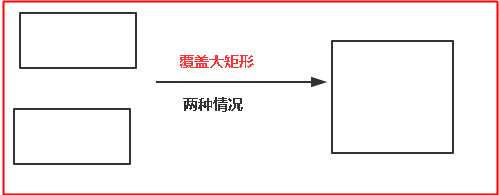
　　假如n=3，那么问题就变成用 3个 2x1 的小矩形无重叠地覆盖一个 2x3 的大矩形，第一种情况，填充的那一块是横着放的，如下所示，那么剩下的需要填充的就是相当于n=2的情况，即2x2的情况；第二种情况就是第一块填充的是竖着放的，那么还需要再填充一块，那么剩下的就是n=1的情况；

             

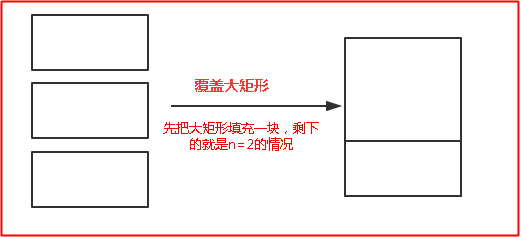
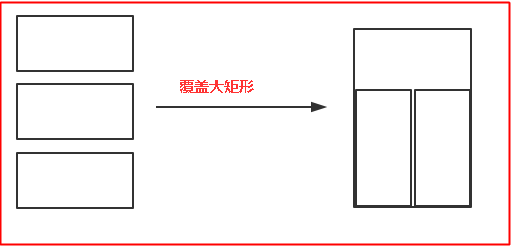
 　　依次类推，当n=5的时候也有两种情况，第一种情况横着填充一块，剩下的就是n=4的那种；第二种情况竖着填充两块，剩下的就是相当于n=3的那种，通用公式如下，就不多说了，代码的话和上面基本一样，就不多说了。。。

 

 　　这两个题目还是很有意思的，可以说一个题目是让你看公式写代码，而另外一个题目其实用的是分治法，所谓的分治法，就是分而治之。就是将原问题划分为n个规模较小，结构与原问题类似的小问题进行处理，递归地解决这些问题，然后再合并求解的过程。