树状数组学习笔记

树状数组学习笔记

P3374 【模板】树状数组 1

//树状数组1

#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

int n, m, t, tree[500007];

int lowbit(int k)
{
	return k & -k;
}

void add(int b, int c)
{
	while(b <= n)
	{
		tree[b] += c;
		b += lowbit(b);
	}
}

int sum(int b)
{
	int ans = 0;
	while(b != 0)
	{
		ans += tree[b];
		b -= lowbit(b);
	}
	return ans;
}

int main() {
	int a, b, c;
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++)
	{
		scanf("%d", &t);
		add(i, t);
	}
	for(int i = 1; i <= m; i++)
	{
		scanf("%d%d%d", &a, &b, &c);
		if(a == 1)
			add(b, c);
		if(a == 2)
			printf("%d
", sum(c) - sum(b - 1));	
	}
	return 0;
} 

结构

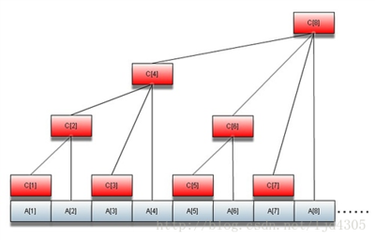
c就是树状数组

单点插入

他们之间的关系如下

[c[1] = a[1] ]

[c[2] = a[1]+a[2] ]

[c[3] = a[3] ]

[c[4] = a[1] + a[2] + a[3] + a[4] ]

好像看不出什么规律

用二进制表示

[c[0001] = a[0001] ]

[c[0010] = a[0010] + a[0001] ]

[c[0011] = a[0011] ]

[c[0100] = a[0100] + a[0010] + a[0011] + a[0001] ]

我们引入lowbit函数

这个函数可以帮我们求出一个数的二进制表示的最后位的1

lowbit求法

int lowbit(int k)
{
	return k & -k;
}

例子

​ $$5 = 0101, 1 = 0001$$

​ $$lowbit(5) = 1$$

void add(int b, int c)
{
	while(b <= n)
	{
		tree[b] += c;
		b += lowbit(b);
	}
}

当我在插入一个数或改变一个数的时候

这个数会影响它后面的每个c数组

所以每次给b加上lowbit(b)来模拟这个数后面的每一个c数组下标

区间求和

int sum(int b)
{
	int ans = 0;
	while(b != 0)
	{
		ans += tree[b];
		b -= lowbit(b);
	}
	return ans;
}

由于c数组是类似于前缀和的东西

所以我们如果求区间a到b的和

输出sum(b) - sum(a - 1)即可

---

P3368 【模板】树状数组 2

//树状数组2
#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

int n, m, op, x, y, z;
int a[500007], p[500007];

int lowbit(int x)
{
	return x & -x;
}

void add(int x, int y)
{
	while(x <= n)
	{
		p[x] += y;
		x += lowbit(x);
	}
}

int chaf(int x)
{
	int ans = 0;
	while(x != 0)
	{
		ans += p[x];
		x -= lowbit(x);
	}
	return ans;
}

int main() {
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++)
		scanf("%d", &a[i]);
	for(int i = 1; i <= m; i++)
	{
		scanf("%d", &op);
		if(op == 1)
		{
			scanf("%d%d%d", &x, &y, &z);
			add(x, z);
			add(y + 1, -z);
		}
		else if(op == 2)
		{
			scanf("%d", &x);
			printf("%d
", a[x] + chaf(x));
		}
	}
	return 0;
}

区间修改

区间修改一般使用差分实现

具体一点是用树状数组维护差分数组

即x到y加z时

add(x, z);
add(y + 1, -z);

单点查询

看代码

---

​ 2019年8月19日还差练习题