在做数字图像处理的时候,特别是PCA降维的时候,很多情况下要遇到协方差矩阵,其实一直糊里糊涂的不知道到底是个什么东西,
以下是我收集的网上资料做的整理和自己的一些理解。
统计学的基本概念
学过概率统计的孩子都知道,统计里最基本的概念就是样本的均值,方差,或者再加个标准差。首先我们给你一个含有n个样本的集合,依次给出这些概念的公式描述,这些高中学过数学的孩子都应该知道吧,一带而过。
均值:

方差:
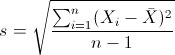
均值方差的意义我就不多说了,均值就是描述样本总体水品的,班级平均分你总归明白的吧。
方差呢就是描述样本稳定性的,比如你的成绩,一会儿全班第一,一会儿不及格,这就是方差很大。张三总是在班级前十,但也没当过第一,这方差就比较小。
那么协方差到底是做什么用的呢?
我们一直在讨论一个随机变量的情况,一个随机变量的均值,一个随机变量的方差,当涉及到两个随机变量的时候,有时候我们要判定他们两个的相关性,协方差的意义就在于此。
我们再回头看方差的定义:

这是描述的一个随机变量,
然后我们看看两个随机变量X,Y,协方差的定义如下:
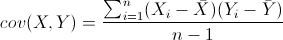
明白了吧,协方差在描述两个随机变量之间的相关度。
基于以上理论,我们明白了协方差的意义。那么协方差矩阵又是做什么的呢?想象一下,两个随机变量X,Y我们可以用协方差表示,那么10个,20个,n个呢。协方差矩阵就产生了。定义n维随机变量Xn=[X1,X2,X3,.....Xn-1,Xn];(其实相当于n个随机变量的集合)
我们用协方差矩阵表示他们互相之间的协方差:
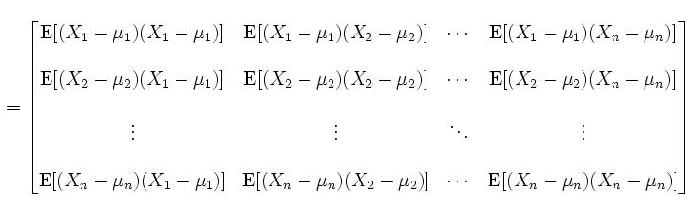
(式中Un表示Xn的均值)
明显这是个对称矩阵,第i行j列,或者j行i列的值,表示Xi与Xj的协方差。
好了,最后,我觉得理解协方差矩阵的关键点在于理解多维随机变量,不同维度之间的协方差,对应起来就是协方差矩阵的元素。