转自:http://www.cnblogs.com/hemiy/p/6155425.html
本人只跑过knn的原始算法,环境是python2.7
正文
---------------------------------------------------------------------------------------
本系列文章为《机器学习实战》学习笔记,内容整理自书本,网络以及自己的理解,如有错误欢迎指正。
源码在Python3.5上测试均通过,代码及数据 --> https://github.com/Wellat/MLaction
---------------------------------------------------------------------------------------
1 算法概述
1.1 算法特点
简单地说,k-近邻算法采用测量不同特征值之间的距离方法进行分类。
优点:精度高、对异常值不敏感、无数据输入假定
缺点:计算复杂度高、空间复杂度高
适用数据范围:数值型和标称型
1.2 工作原理
存在一个训练样本集,并且每个样本都存在标签(有监督学习)。输入没有标签的新样本数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取出与样本集中特征最相似的数据(最近邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,而且k通常不大于20。最后选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
1.3 实例解释
以电影分类为例子,使用k-近邻算法分类爱情片和动作片。有人曾经统计过很多电影的打斗镜头和接吻镜头,下图显示了6部电影的打斗和接吻镜头数。 假如有一部未看过的电影,如何确定它是爱情片还是动作片呢?

①首先需要统计这个未知电影存在多少个打斗镜头和接吻镜头,下图中问号位置是该未知电影出现的镜头数

②之后计算未知电影与样本集中其他电影的距离(相似度),具体算法先忽略,结果如下表所示:
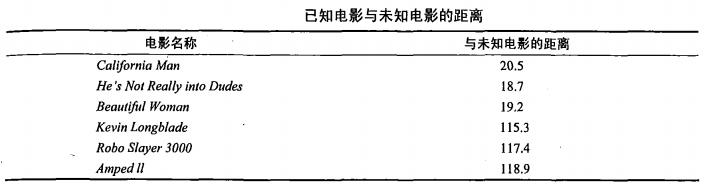
③将相似度列表排序,选出前k个最相似的样本。此处我们假设k=3,将上表中的相似度进行排序后前3分别是:He’s Not Really into Dudes,Beautiful Woman,California Man。
④统计最相似样本的分类。此处很容易知道这3个样本均为爱情片。
⑤将分类最多的类别作为未知电影的分类。那么我们就得出结论,未知电影属于爱情片。
2 代码实现
2.1 k-近邻简单分类的应用
2.1.1 算法一般流程

2.1.2 Python实现代码及注释
1 #coding=UTF8
2 from numpy import *
3 import operator
4
5 def createDataSet():
6 """
7 函数作用:构建一组训练数据(训练样本),共4个样本
8 同时给出了这4个样本的标签,及labels
9 """
10 group = array([
11 [1.0, 1.1],
12 [1.0, 1.0],
13 [0. , 0. ],
14 [0. , 0.1]
15 ])
16 labels = ['A', 'A', 'B', 'B']
17 return group, labels
18
19 def classify0(inX, dataset, labels, k):
20 """
21 inX 是输入的测试样本,是一个[x, y]样式的
22 dataset 是训练样本集
23 labels 是训练样本标签
24 k 是top k最相近的
25 """
26 # shape返回矩阵的[行数,列数],
27 # 那么shape[0]获取数据集的行数,
28 # 行数就是样本的数量
29 dataSetSize = dataset.shape[0]
30
31 """
32 下面的求距离过程就是按照欧氏距离的公式计算的。
33 即 根号(x^2+y^2)
34 """
35 # tile属于numpy模块下边的函数
36 # tile(A, reps)返回一个shape=reps的矩阵,矩阵的每个元素是A
37 # 比如 A=[0,1,2] 那么,tile(A, 2)= [0, 1, 2, 0, 1, 2]
38 # tile(A,(2,2)) = [[0, 1, 2, 0, 1, 2],
39 # [0, 1, 2, 0, 1, 2]]
40 # tile(A,(2,1,2)) = [[[0, 1, 2, 0, 1, 2]],
41 # [[0, 1, 2, 0, 1, 2]]]
42 # 上边那个结果的分开理解就是:
43 # 最外层是2个元素,即最外边的[]中包含2个元素,类似于[C,D],而此处的C=D,因为是复制出来的
44 # 然后C包含1个元素,即C=[E],同理D=[E]
45 # 最后E包含2个元素,即E=[F,G],此处F=G,因为是复制出来的
46 # F就是A了,基础元素
47 # 综合起来就是(2,1,2)= [C, C] = [[E], [E]] = [[[F, F]], [[F, F]]] = [[[A, A]], [[A, A]]]
48 # 这个地方就是为了把输入的测试样本扩展为和dataset的shape一样,然后就可以直接做矩阵减法了。
49 # 比如,dataset有4个样本,就是4*2的矩阵,输入测试样本肯定是一个了,就是1*2,为了计算输入样本与训练样本的距离
50 # 那么,需要对这个数据进行作差。这是一次比较,因为训练样本有n个,那么就要进行n次比较;
51 # 为了方便计算,把输入样本复制n次,然后直接与训练样本作矩阵差运算,就可以一次性比较了n个样本。
52 # 比如inX = [0,1],dataset就用函数返回的结果,那么
53 # tile(inX, (4,1))= [[ 0.0, 1.0],
54 # [ 0.0, 1.0],
55 # [ 0.0, 1.0],
56 # [ 0.0, 1.0]]
57 # 作差之后
58 # diffMat = [[-1.0,-0.1],
59 # [-1.0, 0.0],
60 # [ 0.0, 1.0],
61 # [ 0.0, 0.9]]
62 diffMat = tile(inX, (dataSetSize, 1)) - dataset
63
64 # diffMat就是输入样本与每个训练样本的差值,然后对其每个x和y的差值进行平方运算。
65 # diffMat是一个矩阵,矩阵**2表示对矩阵中的每个元素进行**2操作,即平方。
66 # sqDiffMat = [[1.0, 0.01],
67 # [1.0, 0.0 ],
68 # [0.0, 1.0 ],
69 # [0.0, 0.81]]
70 sqDiffMat = diffMat ** 2
71
72 # axis=1表示按照横轴,sum表示累加,即按照行进行累加。
73 # sqDistance = [[1.01],
74 # [1.0 ],
75 # [1.0 ],
76 # [0.81]]
77 sqDistance = sqDiffMat.sum(axis=1)
78
79 # 对平方和进行开根号
80 distance = sqDistance ** 0.5
81
82 # 按照升序进行快速排序,返回的是原数组的下标。
83 # 比如,x = [30, 10, 20, 40]
84 # 升序排序后应该是[10,20,30,40],他们的原下标是[1,2,0,3]
85 # 那么,numpy.argsort(x) = [1, 2, 0, 3]
86 sortedDistIndicies = distance.argsort()
87
88 # 存放最终的分类结果及相应的结果投票数
89 classCount = {}
90
91 # 投票过程,就是统计前k个最近的样本所属类别包含的样本个数
92 for i in range(k):
93 #