题目传送门
题目描述
暑假期间,小龙报名了一个模拟野外生存作战训练班来锻炼体魄,训练的第一个晚上,教官就给他们出了个难题。由于地上露营湿气重,必须选择在高处的树屋露营。小龙分配的树屋建立在一颗高度为N+1尺(N为正整数)的大树上,正当他发愁怎么爬上去的时候,发现旁边堆满了一些空心四方钢材(如图),经过观察和测量,这些钢材截面的宽和高大小不一,但都是1尺的整数倍,教官命令队员们每人选取N个空心钢材来搭建一个总高度为N尺的阶梯来进入树屋,该阶梯每一步台阶的高度为1尺,宽度也为1尺。如果这些钢材有各种尺寸,且每种尺寸数量充足,那么小龙可以有多少种搭建方法?(注:为了避免夜里踏空,钢材空心的一面绝对不可以向上。)
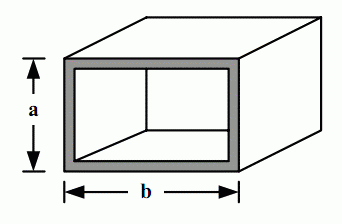
输入格式
一个正整数N,表示阶梯的高度。
输出格式
一个正整数,表示搭建方法的个数。(注:搭建方法个数可能很大。)
样例
样例输入
3
样例输出
5
数据范围与提示
样例说明:
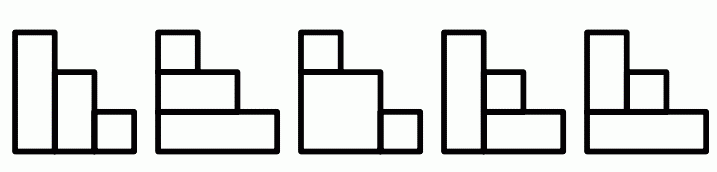
数据范围:
对于全部数据,$N leqslant 100$。
题解
根据个人做题经验,看到样例输入3,样例输出5,优先考虑卡特兰数。
根据数据范围,可以使用分解质因数和高精度两种做法求出卡特兰数。
代码时刻
分解质因数+高精乘低精:
#include<bits/stdc++.h>
using namespace std;
int n;
int pre[2000001],pri[2000001];
int wzc[2000001];
int l=1;
long long ans[100001],flag1,flag2;
void pre_work()
{
ans[1]=1;
for(int i=2;i<=2*n;i++)
{
if(!pri[i])
{
pri[i]=i;
pre[++pre[0]]=i;
}
for(int j=1;j<=pre[0];j++)
{
if(pre[j]>pri[i]||i*pre[j]>2*n)break;
pri[i*pre[j]]=pre[j];
}
}
}
void mul(int x)
{
flag2=0;
for(int i=1;i<=l;i++)
{
flag1=ans[i]*x;
ans[i]=flag1%1000000000000000+flag2;
flag2=flag1/1000000000000000;
}
if(flag2)ans[++l]=flag2;
}
int main()
{
scanf("%d",&n);
pre_work();
for(int i=n+2;i<=2*n;i++)
{
int flag=i;
while(flag>1)
{
wzc[pri[flag]]++;
flag/=pri[flag];
}
}
for(int i=2;i<=n;i++)
{
int flag=i;
while(flag>1)
{
wzc[pri[flag]]--;
flag/=pri[flag];
}
}
for(int i=1;i<=2*n;i++)
for(int j=1;j<=wzc[i];j++)
mul(i);
printf("%lld",ans[l]);
while(--l)printf("%.15lld",ans[l]);
return 0;
}
高精度:
#include<bits/stdc++.h>
using namespace std;
int n,m;
long long a[100000],c[100000];
int mu[5001];
void mul(register int p)
{
register int x=0,j;
for(j=1;j<=a[0];j++)
{
a[j]=a[j]*p+x;
x=a[j]/10;
a[j]%=10;
}
a[j]=x;
while(a[j]>9)
{
a[j+1]=a[j]/10;
a[j]%=10;
j++;
}
while(a[j]==0&&j>1)j--;
a[0]=j;
}
void chu(register int b)
{
register int x=0,s=0,t=0;
memset(c,0,sizeof(c));
for(register int i=1;i<=a[0];i++)
{
x=x*10+a[i];
if(x/b!=0)s++;
if(s==0)continue;
c[++t]=x/b;
x%=b;
}
for(register int i=1;i<=t;i++)
a[i]=c[i];
a[0]=t;
}
int main()
{
a[0]=a[1]=1;
scanf("%d",&n);
for(register int i=n+2;i<=2*n;i++)mul(i);
reverse(a+1,a+a[0]+1);
for(register int i=2;i<=n;i++)chu(i);
for(register int i=1;i<=a[0];i++)printf("%d",a[i]);
}
rp++