题目传送门(内部题23)
输入格式
第一行有$2$个整数$n,m$。
接下来有$n$行,每行$m$个整数,表示$a$数组。
接下来有$n$行,每行$m$个整数,表示$b$数组。
输出格式
一行一个整数表示答案。
样例
样例输入:
3 3
0 6 8
1 6 1
0 6 8
0 1 2
3 4 5
0 6 7
样例输出:
21
数据范围与提示
样例解释:
最优路径$(2,3)
ightarrow (3,2)
ightarrow (3,3)$。
最优答案$5+6+7+|3-2|+|2-3|+|3-3|+|3-2|=21$。
数据范围:
对于所有数据,$1leqslant n,mleqslant 2 imes {10}^3,0leqslant a_ileqslant {10}^6,0leqslant b_ileqslant {10}^6$。
保证至少存在一个地区$a[i][j]>0$,所有$a[i][j]=0$的地区满足$b[i][j]=0$。
题解
首先,为使国王心情更舒畅,我们所要规划的路线一定是在离散化之后$a[i][j]$每次只增加$1$的一条路线,那么你可能会想到建边跑最长路,但是显然这样就$TLE$掉了。
所以我们考虑$DP$,定义$dp[i][j]$表示到达点$(i,j)$的最大吸引度之和。
那么我们可以暴力转移,枚举每一个点,最劣时间复杂度是$Theta(n^2m^2)$,还是不行。
所以考虑进行优化。
考虑对于点$(i,j)$,要从点$(i',j')$转移得来,那么将分为下面四种情况:
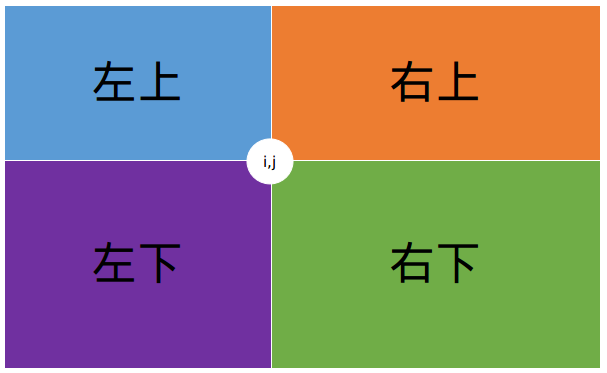
可能从左上,右上,左下,右下四个方向进行转移。
那么你可能会想到用二维树状数组,时间复杂度:$Theta(n imes m imes log n imes log m)$,这样你就拿到了$80$分。
那么考虑满分算法。
分别维护四个最大值:
$(1,1)−(i,j):dp[i'][j']−i−j$的最大值。
$(1,j)−(i,m):dp[i'][j']−i+j$的最大值。
$(i,1)−(n,j):dp[i'][j']+i−j$的最大值。
$(i,j)−(n,m):dp[i'][j']+i+j$的最大值。
转移的时候从这$4$个最大值中转直接转移过来即可。
那你可能会存在疑问,如果$(i',j')$在$(i,j)$的左上方,但是我们却从维护的左下角中的最大之中转移过来了怎么办?
我会告诉你,这种状况是一定不会发生的,仔细计算一下即可发现从右下转移一定没有从左上转移得到的值更大。
到此这道题就轻松解决了。
对于下面我的代码,我把所有有$a[i][j]$的点压入了队列,然后进行排序,所以$dp$只有一维。
时间复杂度:$Theta(n imes m)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
struct node{long long x,y,v,w;}que[4000001];
int n,m;
long long a[2001][2001],b[2001][2001];
long long num,prem[4],maxn[4];
long long dp[4000001];
long long ans;
bool cmp(node a,node b){return a.v<b.v;}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%lld",&a[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
scanf("%lld",&b[i][j]);
if(a[i][j])que[++num]=(node){i,j,a[i][j],b[i][j]};
}
sort(que+1,que+num+1,cmp);
int lft;
dp[1]=que[1].w;
maxn[0]=max(maxn[0],dp[1]+que[1].x+que[1].y);
maxn[1]=max(maxn[1],dp[1]-que[1].x+que[1].y);
maxn[2]=max(maxn[2],dp[1]+que[1].x-que[1].y);
maxn[3]=max(maxn[3],dp[1]-que[1].x-que[1].y);
for(int i=2;i<=num;i++)
{
if(que[i].v!=que[i-1].v)
{
lft=i;
break;
}
dp[i]=que[i].w;
maxn[0]=max(maxn[0],dp[i]+que[i].x+que[i].y);
maxn[1]=max(maxn[1],dp[i]-que[i].x+que[i].y);
maxn[2]=max(maxn[2],dp[i]+que[i].x-que[i].y);
maxn[3]=max(maxn[3],dp[i]-que[i].x-que[i].y);
}
for(int i=lft;i<=num;i++)
{
if(que[i].v!=que[i-1].v)
for(int j=0;j<4;j++)
{
prem[j]=maxn[j];
maxn[j]=0;
}
dp[i]=max(max(prem[0]-que[i].x-que[i].y,prem[1]+que[i].x-que[i].y),max(prem[2]-que[i].x+que[i].y,prem[3]+que[i].x+que[i].y))+que[i].w;
maxn[0]=max(maxn[0],dp[i]+que[i].x+que[i].y);
maxn[1]=max(maxn[1],dp[i]-que[i].x+que[i].y);
maxn[2]=max(maxn[2],dp[i]+que[i].x-que[i].y);
maxn[3]=max(maxn[3],dp[i]-que[i].x-que[i].y);
}
for(int i=1;i<=num;i++)
ans=max(ans,dp[i]);
cout<<ans<<endl;
return 0;
}
rp++