题目传送门(内部题51)
输入格式
第一行一个整数$t$表示数据组数。
每组数据的第一行有三个整数$s,k,n$。
第二行有$n$个整数$A_1,A_2,...,A_n$,依次表示黑白条的长度。
输出格式
若能通过输出$"TAK"$,否则输出$"NIE"$。
样例
样例输入:
2
2 8 7
2 5 6 3 2 1 2
2 8 4
1 6 7 4
样例输出:
TAK
NIE
数据范围与提示
样例解释:
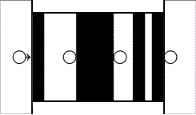
数据范围:
$30\%$的数据,$nleqslant 1300$;
$50\%$的数据,$nleqslant 22,000$;
$100\%$的数据,$2leqslant nleqslant 500,000,1leqslant s<kleqslant {10}^9,1leqslant A_ileqslant {10}^9,1leqslant tleqslant 10$。
数据有梯度。输入文件较大请使用读入优化。
题解
其实就是一个贪心,主要是策略很难想。
首先来处理脚的长度,我们可以将所有的黑块都延长$s$,所有的白块左端点向右移动$s$,这样就相当与忽略了脚的长度。
然后会有一些特判的情况,对于我的贪心策略,我们只需要用到当一个黑块长度大于$k$时,肯定跳不过去,所以直接输出$"NIE"$即可。
现在来讲对于一般情况,我是如何判断的。
首先,将所有的黑块的左端点和右端点分别$mod k$,那么我们是不能在这段区间进行起跳的;如果出现$mod k$完之后右端点小于左端点,那么区间$[0,r]$和区间$[l,k-1]$是不能起跳的。
之后我们只需要将所有的不能跳的区间排个序,然后我们只需要找到一个可以起跳的点即可。
细节比较多,慢慢调吧……
时间复杂度:$Theta(nlog n)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
struct rec{long long l,r;}e[10000000];
long long s,k,n;
long long sum[5000001];
long long lft[5000001],rht[5000001],wsq;
int top;
bool flag;
bool cmp(rec a,rec b){return a.l==b.l?a.r<b.r:a.l<b.l;}
int main()
{
int T;scanf("%d",&T);
while(T--)
{
scanf("%lld%lld%lld",&s,&k,&n);
top=flag=wsq=0;
for(int i=1;i<=n;i++)
{
long long a;
scanf("%lld",&a);
if(i&1)a+=s;
else{a-=s;a%=k;}
if(a>k)flag=1;
sum[i]=sum[i-1]+a;
if(i&1)
{
lft[i]=sum[i-1]+1;
rht[i]=sum[i]-1;
}
}
if(((n&1)&&sum[n]<=k)||((!(n&1))&&sum[n-1]<=k)){puts("TAK");continue;}
if(flag){puts("NIE");continue;}
for(int i=1;i<=n;i+=2)
{
lft[0]=lft[i]%k;
rht[0]=rht[i]%k;
if(rht[0]<lft[0])
{
e[++top]=(rec){0,rht[0]};
e[++top]=(rec){lft[0],k-1};
}
else e[++top]=(rec){lft[0],rht[0]};
}
sort(e+1,e+top+1,cmp);
if(e[1].l){puts("TAK");goto nxt;}
for(int i=1;i<=top;i++)
{
if(wsq+1<e[i].l){puts("TAK");goto nxt;}
wsq=max(wsq,e[i].r);
}
if(wsq<k-1){puts("TAK");continue;}
puts("NIE");
nxt:;
}
return 0;
}
rp++