题目描述
在比特镇一共有$n$家商店,编号依次为$1$到$n$。每家商店只会卖一种物品,其中第$i$家商店的物品单价为$c_i$,价值为$v_i$,且该商店开张的时间为$t_i$。
$Byteasar$计划进行$m$次购物,其中第$i$次购物的时间为$T_i$,预算为$M_i$。每次购物的时候,$Byteasar$会在每家商店购买最多一件物品,当然他也可以选择什么都不买。如果购物的时间早于商店开张的时间,那么显然他无法在这家商店进行购物。
现在$Byteasar$想知道,对于每个计划,他最多能购入总价值多少的物品。请写一个程序,帮助$Byteasar$合理安排购物计划。
注意:每次所花金额不得超过预算,预算也不一定要花完,同时预算不能留给其它计划使用。
输入格式
第一行包含两个正整数$n,m$,表示商店的总数和计划购物的次数。
接下来$n$行,每行三个正整数$c_i,v_i,t_i$,分别表示每家商店的单价、价值以及开张时间。
接下来$m$行,每行两个正整数$T_i,M_i$,分别表示每个购物计划的时间和预算。
输出格式
输出$m$行,每行一个整数,对于每个计划输出最大可能的价值和。
样例
样例输入:
5 2
5 5 4
1 3 1
3 4 3
6 2 2
4 3 2
3 8
5 9
样例输出:
10
12
数据范围与提示
样例解释:
第一个计划可以在商店$2,3,5$各购买一件物品,总花费为$1+3+4=8$,总价值为$3+4+3=10$。
第二个计划可以在商店$1,2,3$各购买一件物品,总花费为$5+1+3=9$,总价值为$5+3+4=12$。
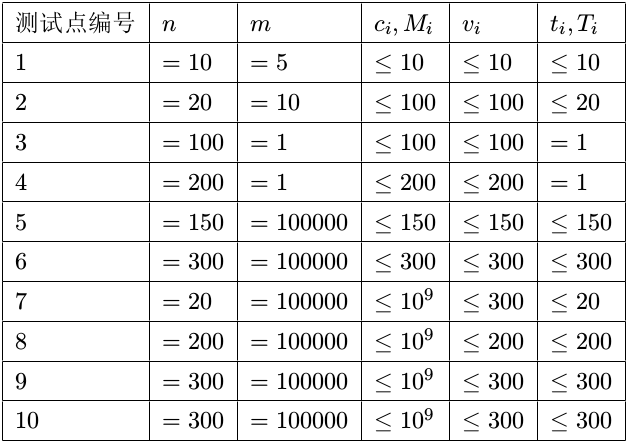
数据范围:
对于$100\%$的数据,$1leqslant t_i,T_ileqslant n$。
题解
对于正常的背包$DP$,我们都是设$dp[i][j]$表示选到第$i$个,背包空间为$j$所能获得的最大价值。
而对于这道题,背包空间很大,但是价值很小,所以我们不妨设$dp[i][j]$表示选到第$i$个,得到价值为$j$所消耗的最小背包空间。
对于时间,我们可以将物品和询问按时间排序,统一计算答案,然后在二分提取询问即可。
时间复杂度:$Theta(n^2v+mlog m)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
struct rec{int c,v,t;}e[301];
struct node{int t,m,id;}q[100001];
int n,m;
int dp[100000];
int ans[100001];
bool cmp1(rec a,rec b){return a.t<b.t;}
bool cmp2(node a,node b){return a.t<b.t;}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d%d%d",&e[i].c,&e[i].v,&e[i].t);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&q[i].t,&q[i].m);
q[i].id=i;
}
sort(e+1,e+n+1,cmp1);
sort(q+1,q+m+1,cmp2);
memset(dp,0x3f,sizeof(dp));
dp[0]=0;
int j=1;
for(int i=1;i<=m;i++)
{
while(j<=n&&e[j].t<=q[i].t)
{
for(int k=n*300;k>=e[j].v;k--)
dp[k]=min(dp[k],dp[k-e[j].v]+e[j].c);
for(int k=n*300;k;k--)
dp[k]=min(dp[k],dp[k+1]);
j++;
}
ans[q[i].id]=upper_bound(dp+1,dp+n*300+1,q[i].m)-dp-1;
}
for(int i=1;i<=m;i++)
printf("%d
",ans[i]);
return 0;
}
rp++