题目背景
$Maxtir$最喜欢最大值。
题目传送门(内部题128)
输入格式
第$1$行输入四个正整数$n,m,q$。
第$2$至$n+1$行中,第$i+1$行输入魔法晶石$i$的三种属性$(x_i,y_i,p_i)$。
接下来$q$行,每行两个正整数$l_i,r_i$,数据保证$[l_i,r_i]$互不包含。
输出格式
输出一行一个正整数$ans$表示答案。
样例
样例输入:
3 3 2
1 1 500000004
2 2 333333336
3 3 1
1 2
2 3
样例输出:
4
数据范围与提示
样例解释:
$500000004equivfrac{1}{2}mod(10^9+7),333333336equivfrac{1}{2}mod(10^9+7)$
最终的魔法阵中的晶石序列可能是
$(otimes,otimes,3),(otimes,2,3),(1,otimes,3),(1,2,3)$四种,他们的概率分别是$frac{1}{3},frac{1}{6},frac{1}{3},frac{1}{6}$
两次吸取的能量分别是$(0,3),(2,3),(1,3),(2,3)$,最终的答案是$3 imesfrac{1}{3}+5 imesfrac{1}{6}+4 imesfrac{1}{3}+5 imesfrac{1}{6}=4$
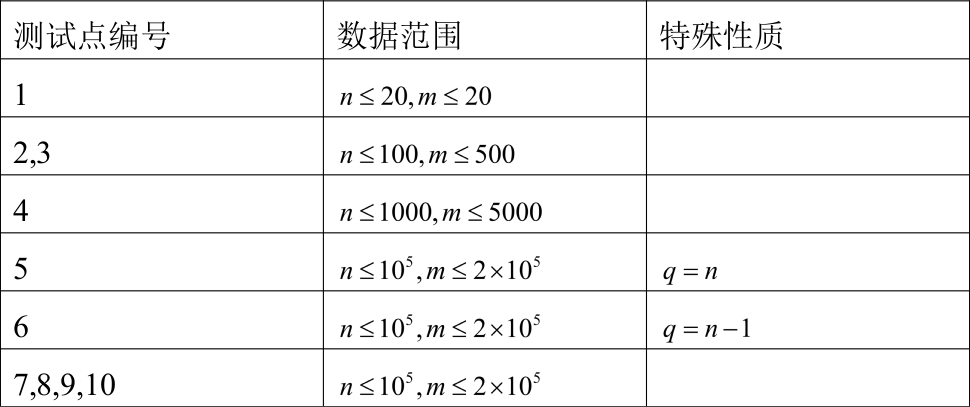
数据范围:
对于$100\%$的数据,满足$0leqslant y_ileqslant 10^9,1leqslant qleqslant n,0leqslant p_i<10^9+7$
题解
先从$30\%$的部分分入手($10\%$的暴力真的没什么技术含量)。
因为每个魔法阵要取最小值,所以不妨将魔法晶石从大到小排序。
一个魔法晶石能做贡献当且仅当它出现且比它小的都没有出现(当前魔法阵)。
所以考虑这种状态出现的概率,也就是求$P(maxlimits_{i=l}^rv_igeqslant x)$;化一下式子,即可得到$1-prodlimits_{i=l}^r1-P(v_igeqslant x)$。
所以我们可以把小于$x$的数不选的概率乘起来再减去所有数都不选的概率,即$P(v_igeqslant x)$。
考虑怎么优化,每次更改的贡献就是$1-P(v_igeqslant y) ightarrow 1-P(v_igeqslant x)$。
但是我们可以只考虑$q=prodlimits_{i=l}^r1-P(v_igeqslant x)$,这样就可以$Theta(log n)$修改了。
想办法利用性质区间互不包含。
将所有区间按左端点排序,就可以实现点和区间的转化了利用线段树优化即可。
时间复杂度:$Theta(mlog q)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
#define L(x) x<<1
#define R(x) x<<1|1
using namespace std;
const int mod=1000000007;
struct rec{int x,y,p;}f[200001];
struct node{int nxt,to;}e[400001];
int head[200001],cnt;
int n,m,q;
int l[200001],r[200001];
long long b[200001];
long long tr[400001],lz[400001];
pair<int,int> p[200001];
long long ans;
bool cmp(rec a,rec b){return a.y<b.y;}
void add(int x,int p)
{
e[++cnt].nxt=head[x];
e[cnt].to=1LL*e[head[x]].to*(1-p)%mod;
head[x]=cnt;
}
long long qpow(long long x,long long y)
{
long long res=1;
while(y)
{
if(y&1)res=res*x%mod;
x=x*x%mod;y>>=1;
}
return res;
}
void pushup(int x){tr[x]=(tr[L(x)]+tr[R(x)])%mod;}
void build(int x,int l,int r)
{
lz[x]=1;
if(l==r){tr[x]=1;return;}
int mid=(l+r)>>1;
build(L(x),l,mid);
build(R(x),mid+1,r);
pushup(x);
}
void pushdown(int x)
{
tr[L(x)]=lz[x]*tr[L(x)]%mod;
tr[R(x)]=lz[x]*tr[R(x)]%mod;
lz[L(x)]=lz[x]*lz[L(x)]%mod;
lz[R(x)]=lz[x]*lz[R(x)]%mod;
lz[x]=1;
}
void change(int x,int l,int r,int L,int R,int w)
{
if(r<L||R<l)return;
if(L<=l&&r<=R){tr[x]=tr[x]*w%mod;lz[x]=lz[x]*w%mod;return;}
int mid=(l+r)>>1;
pushdown(x);
change(L(x),l,mid,L,R,w);
change(R(x),mid+1,r,L,R,w);
pushup(x);
}
void change(int x)
{
if(r[x]<l[x])return;
int res=qpow(1-(e[head[x]].to-b[x])%mod,mod-2);
head[x]=e[head[x]].nxt;
change(1,1,q,l[x],r[x],(1-e[head[x]].to+b[x])*res%mod);
}
int main()
{
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=m;i++)scanf("%d%d%d",&f[i].x,&f[i].y,&f[i].p);
for(int i=1;i<=q;i++)scanf("%d%d",&p[i].first,&p[i].second);
sort(f+1,f+m+1,cmp);cnt=n;
for(int i=1;i<=n;i++){e[i].to=1;head[i]=i;}
for(int i=1;i<=m;i++)add(f[i].x,f[i].p);
for(int i=1;i<=n;i++)b[i]=e[head[i]].to;
int fl=1,fr=0;
for(int i=1;i<=n;i++)
{
while(fl<=fr&&p[fl].second<i)fl++;
while(p[fr+1].first<=i&&fr<q)fr++;
l[i]=fl;r[i]=fr;
}
build(1,1,q);
for(int i=m,j;i;i=j)
{
for(j=i;f[i].y==f[j].y&&j;j--)change(f[j].x);
ans=(ans+tr[1]*(f[i].y-f[j].y))%mod;
}
ans=(1LL*f[m].y*q-ans)%mod;
printf("%d
",(ans+mod)%mod);
return 0;
}
rp++