553. Optimal Division

Given a list of positive integers, the adjacent integers will perform the float division. For example, [2,3,4] -> 2 / 3 / 4.

However, you can add any number of parenthesis at any position to change the priority of operations. You should find out how to add parenthesis to get the maximum result, and return the corresponding expression in string format. Your expression should NOT contain redundant parenthesis.

Example:

Input: [1000,100,10,2]
Output: "1000/(100/10/2)"
Explanation:
1000/(100/10/2) = 1000/((100/10)/2) = 200
However, the bold parenthesis in "1000/((100/10)/2)" are redundant, 
since they don't influence the operation priority. So you should return "1000/(100/10/2)". 
Other cases:
1000/(100/10)/2 = 50
1000/(100/(10/2)) = 50
1000/100/10/2 = 0.5
1000/100/(10/2) = 2

Note:

1. The length of the input array is [1, 10].
2. Elements in the given array will be in range [2, 1000].
3. There is only one optimal division for each test case.

题目含义：给定一组正数并依次做除法，你可以添加任意数量的括号，使得结果最大。返回加了括号以后的字符串

思路：

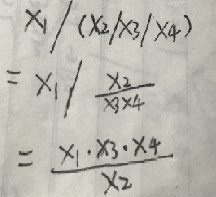
存在这样一个基本事实：X1/X2/X3/……/Xn = X1/X2*Y，也就是说对于X1/X2/X3/……/Xn，无论怎样加括号，总是可以表示成X1/X2*Y的形式。若要使得X1/X2/X3/……/Xn的值最大，则Y值应该最大。当Y=X3*x4……*Xn时，可以得到最大值。

　　当Y为最大值时，X1/X2*Y = X1*X3*X4……*Xn/X2 = X1/（X2/X3/X4……/Xn）。

    public String optimalDivision(int[] nums) {
        StringBuilder builder = new StringBuilder();
        builder.append(nums[0]);
        for (int i = 1; i < nums.length; i++) {
            if (i == 1 && nums.length > 2) {
                builder.append("/(").append(nums[i]);
            } else {
                builder.append("/").append(nums[i]);
            }
        }

        return nums.length > 2 ? builder.append(")").toString() : builder.toString();        
    }