1. Github项目地址:https://github.com/ZiJiaW/SudokuGame
GUI在BIN目录下的SudokuGUI.rar中,解压后打开SudokuGame.exe即可。
2. PSP表格:
| PSP2.1 | Personal Software Process Stages | 预估耗时 | 实际耗时 |
| Planning | 计划 | 2h | 2h |
| .Estimate | 估计这个任务需要多少时间 | 1h | 1h |
| Development | 开发 | 35h | 37h |
| .Analysis | 需求分析 | 2h | 3h |
| .Design Spec | 生成设计文档 | 1h | 0.5h |
| .Design Review | 设计复审 | 1h | 1.5h |
| .Design | 代码规范 | 0.5h | 0.5h |
| .Coding | 具体设计 | 5h | 6h |
| .Code Review | 具体编码 | 20h | 23h |
| .Test | 代码复审 | 2.5h | 2.5h |
| Reporting | 测试 | 3h | 2h |
| .Test Report | 报告 | 1h | 1h |
| .Size Measurement | 测试报告 | 1h | 1h |
| .Coding Standard | 计算工作量 | 0.5h | 0.5h |
| .Postmeortem &ProcessImprovementPlan | 事后总结,并提出过程改进计划 | 0.5h | 1h |
| 合计 | 40h | 43h |
3. 看教科书和其它资料中关于Information Hiding, Interface Design, Loose Coupling的章节,说明在结对编程中是如何利用这些方法对接口进行设计的
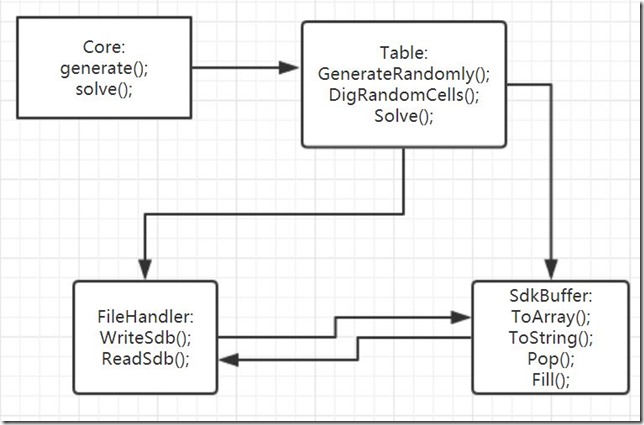
Information Hiding顾名思义就是信息隐藏,也就是说对于函数的使用者来说,不必考虑函数的内部实现就可以顺利地使用它,在结对编程中这是十分必要的,我觉得就是一种Interface Design,两人甚至多人合作下能够很好的分工靠的就是良好的函数封装。LosseCoupling就是松耦合,要求各个类的接口不甚复杂,这样互相配合的时候不需要更多的考虑,简单来说就是两个函数之间的依赖程度,比如一个函数要调用的三个函数之中有一个函数做了修改,那么另外两个函数能够不需要修改正常工作,就达到了松耦合的基本目的:降低代码修改的难度。我们对类的外部接口的设计完全采用信息隐藏的手段,所有涉及到底层实现的函数和变量均为私有的,这样调用者不需要考虑函数细节。对于模块的松耦合,我们的Core模块主要调用Table模块进行数独的生成,下面是两个模块的类设计:
// Core _declspec(dllexport) int sum(int a, int b); _declspec(dllexport) void generate(int number, int mode, int result[][81]); _declspec(dllexport) void generate(int number, int lower, int upper, bool unique, int result[][81]); _declspec(dllexport) bool solve(int puzzle[], int solution[]); _declspec(dllexport) void generate(int number, int result[][81]); // Table extern const unsigned int BufferSize; class Table { private: int cells[9][9]; public: /* 1.This class is used to generate or solve sudokus in large amount. 2.Use Generate to generate and it overrides with different destinations.Solve also overrides. 3.Solve(SdkBuffer*) will modify the input to tell you the result.If an sudoku is not solvable,it will remain as it was.The Solve function will return the number of sudokus tha can be solved. */ Table(); void Generate(unsigned int total, SdkBuffer* sdb); void GenerateRandomly(unsigned int total, SdkBuffer * sdb); void Generate(unsigned int total, FileHandler* fh); void GenerateRandomly(unsigned int total, FileHandler* fh); int Solvable(SdkBuffer* sdb, int index); unsigned int Solve(SdkBuffer* pBoard); //Modified:Solve(SdkBuffer* src,SdkBuffer* dst)==> Solve(SdkBuffer* pBoard); void Solve(FileHandler* src, FileHandler*dst); void DigRandomCells(SdkBuffer* pBoards,unsigned int lower, unsigned int upper,bool isAnswerUnique); ~Table(); private: /* */ void setZero(); void digSpecNum(int[][9],unsigned int num); void digSpecNumUniquely(int[][9], unsigned int num); unsigned int startSolving(unsigned int maxAnswer,SdkBuffer*pResult); void solve(int subt, int num,unsigned int &total,unsigned int &top,SdkBuffer* pResult); int* lookUp(int rst, int cst, int num); };
可以看到Table类的对外函数均是高度封装的,这样Core调用的时候是很方便的,同样对于Table的内部实现来说,主要使用dig方法,这些私有方法的实际长度均很短,也就是说要改变其中一个函数是很方便的事,其他的调用基本不需要改变。以及下面的随机生成数独的代码也体现了松耦合的思想。
4. 计算模块接口的设计与实现过程
1. 需求分析
- -c,-s的要求不变
- 新增-n要求,可带参数组合:-n –r –u; –n –r; –n –u; –n -m;
- -n参数范围1-10000
- -r参数格式:lower~upper 范围20~55
- -m参数范围1-3
- -u不带参数
2. 设计实现
由于我们俩在个人项目中生成数独的方法都是回溯,因此是不满足考虑用户体验的随机生成的,因此在-n的实现中,我们采用了随机生成第一行排列的方法,生成这样的数独终局再进行挖空满足-r要求,这里会出现数量一大就生成重复排列的问题,于是设置了判重函数,下面给出代码解释这里的运作模式:
bool IsDiffer(int line[9], int(*record)[9], int nowsize) { for (int i = 0; i < nowsize; i++) { bool r = true; for (int j = 0; j < 9; j++) { r &= line[j] == record[i][j]; } if (r) return false; } return true; } void Shuffle(int line[9], int(*record)[9], int nowsize) { int r, mid; do { for (int i = 8; i >= 0; i--) { r = rand() % (i + 1);//0-i mid = line[i]; line[i] = line[r]; line[r] = mid; } } while (!IsDiffer(line, record, nowsize)); } void Table::GenerateRandomly(unsigned int total, SdkBuffer* sdb) { srand(clock()); int firstLine[] = { 1,2,3,4,5,6,7,8,9 }; int(*record)[9] = new int[total][9]; setZero(); for (unsigned int i = 0; i < total; i++) { Shuffle(firstLine,record,i); for (int j = 0; j < 9; j++) { cells[0][j] = firstLine[j]; record[i][j] = firstLine[j]; } startSolving(1, sdb); } delete[] record; }
这里实现了三个函数以实现松耦合的设计模式,第一个函数IsDiffer用于判断line是否和记录中生成的排列重复,重复则返回false;第二个函数Shuffle用于生成一个和之前没有重复的排列,利用do-while循环进行判断,其中生成随机排列的算法是用的交换法;最后GenerateRandomly函数调用Shuffle实现生成随机数独终局。
这样我们就生成了可供挖空的并且解不重复的数独终局若干个;对于不指定-u的-r指令来说,十分简单,只需要按顺序取数独终局然后随机进行挖空就可;对于指定生成唯一解的-r要求,经过我们的分析讨论没有什么好方法,只能通过每次挖空都是用solve函数判断是否有多解,在这里我们实现了一个指定最大生成解数量的solve重载,指定最大生成解为2,判断返回值即可确定一个局是否唯一解,代码十分trivial,就不贴了,并没有高深的算法。
接下去我们考虑如何生成一定难度的数独题目,首先考虑用户体验,我们决定所有生成的数独题目都是唯一解的,这也是标准数独的要求,非唯一解的数独都是不标准的,而且解得过程中无法确定化,必须猜解;因此最简单的生成难度就是指定挖空数量范围,使用-r,-u参数就可以完成。但是实际上,挖空数量多的数独并不一定比挖空数量少的数独难(我俩解了几个数独亲身体验了一下),因此考虑在挖了一定数量的空以后在判断这样一个数独是否是我们要求的难度,我们需要一个难度评估模块;
那么这个模块怎么评估难度呢?我们一开始认为可以通过解数独的过程中回溯的次数来评估,然后否决了这个方式,因为这和正常人解数独的过程是不同的,正常人不会采用反人类式的试填,而是会通观大局,先寻找最好填的,即某格只有一个候选数,或是某数在某行只在一个位置作为候选数出现了,前者在数独策略中称为NakedSingle,后者为HiddenSingle,我们觉得可以通过让计算机使用人解数独的策略来解数独,判断各种策略使用的比例,数量,以及这些策略能否解出数独来判断难度。
于是我们实现了下面这个类:
class DifficultyEvaluation { public: DifficultyEvaluation(); ~DifficultyEvaluation(); Difficulty Evaluate(int p[][9]); void GetPuzzle(int p[][9]); private: int puzzle[9][9]; // candidate[i][j][num]==1 means num is candidate to puzzle[i][j]. // candidate[i][j][0]==k means puzzle[i][j] has k candidates. int candidate[9][9][10]; // 唯余法排除:某位置出现某数,则同行/宫/列其他位置该数排除候选 void UpdateSingle(); // 宫内排除:宫内某数只出现在某行/列,则该行/列其他位置该数排除候选 void UpdateCell(); // 行/列/宫显性数对排除法: // 行/列/宫某两个位置只出现两个相同的候选数,则若行列内则排除同行列的其余位置这两个数的候选 // 若这两个位置同宫,则还可排除宫内与两个位置同行列的其余位置这两个数的候选 void UpdateNakedPair(); // 行/列/宫隐性数对排除法: // 某两个数只出现在某行/列/宫的两个位置,则两位置其余候选数排除 void UpdateHiddenPair(); // X-Wing排除法: // 若某数在某两行/列中只出现在该两行/列的两个相同位置,则构成X-Wing,排除四边形边上所有位置的该数候选 void UpdateXWing(); void CandidateDelete(int row, int col, int num); void PuzzleInit(int p[][9]); bool IsFinished(); void Fill(int row, int col, int num); bool FillNakedSingle(); bool FillHiddenSingle(); bool TryToFill(int &updateCount, int &fillCount1, int &fillCount2); };
由于时间有限,我们只实现了以上的几种解题策略,大致的评估算法如下:
1. 两种填数策略(NakedSingle, HiddenSingle)用于根据现有候选数表进行填数,如果成功填数,则用数独规则更新候选数表,再次尝试;
2. 如果填数失败,依次使用更高级的候选数表更新方法排除候选数,如上面声明的几个Update函数,每Update一次尝试一次填数,成功的做法同2;
3. 如果一次循环中用尽了所有更新方法都没办法填一个数,我们认为这个数独题目是Hard难度;
4. 对于现有方法能解出的数独,我们通过判断各种方法生效的次数和两种填数法使用的比例界定难度;
我们认为HiddenSingle难于NakedSingle,实际上我们使用网上的简单难度数独进行测试,发现可以直接全部使用规则排除和NakedSingle解出来;
而找到一些中等难度的数独可能需要十几次的NakedSingle解出,而一些Hard难度的题一部分可以通过高级策略解出,还有一部分我们实现的方法解不出。
因此根据这个大纲我们实现了数独难度评估模块,每次挖出一个数独后传入Evaluate函数进行判断,如果不满足条件则重新生成一个。实际上这样的方法如果穷尽所有解数独的策略,我们就可以不使用回溯(包括DLX)解数独了……软件SudokuExplainer(http://diuf.unifr.ch/pai/people/juillera/Sudoku/Sudoku.html)就能通过确定的方法给出解任何唯一解数独的每一个步骤并评估难度。我们在实现的过程中多次用这个软件玩数独==
这样做的缺点是生成数独的速度会特别慢,比如生成中等难度的数独100个需要5s,Hard难度的数独100个需要18s……感觉要炸。
以上是完成了命令行参数输入部分,对于core的接口,因为上面的实现使用的类遵循松耦合的设计思路,我们只需要调用SdkBuffer的方法将存储的数独终局输出到数组而不是文件中即可,十分方便。
5. 画出UML图显示计算模块部分各个实体之间的关系(画一个图即可)
6. 计算模块接口部分的性能改进
具体按照上面的思路实现完成后,我们发现实现的-r参数在生成唯一解数独时速度过慢,特别是挖超过50个空并且要求唯一解的时候,经过我们讨论,我们的生成方法是每次随机挖一个空,然后对这个数独进行求解,若求解出来有多个解,则将这个空填上,再从剩余的位置随机挖;这里有一个问题就是一旦我们的程序挖出一个唯一解的x空数独,这x个空是不可能被回填的,这就有可能出现对于给定的x个空,任意多挖一个空都会导致数独多解,进入死循环。
因此,我们考虑了一个算法,如果生成的数独多解,我们把这些数独的前十个(小于10就把所有解)存入数组,判断这些数独挖的空中填的数差别最大(重复数最少)的一个格子,将这个格子填上解中该格子出现次数最少的数,这样可以减少这个数独的解,这是StackOverFlow上一个人提到的方法。这样改进后我们就解决了这个问题。对于生成指定难度的数独,我们的生成速度也很慢,这是由于我们除了要生成唯一解的数独以外,还要将这一数独放入评估程序进行评估,两重筛选,但是由于这次作业重视用户体验,我们认为这是可以接受的,实际上在数独游戏调用dll的时候我们只需要生成一个数独就可以了。
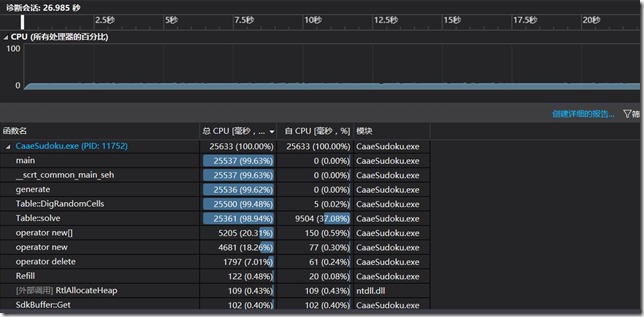
在这上面我们花费了大约3个多小时的时间,下面是一张性能分析图,参数为-n 1000 –r 40~55 -u
可以看到solve函数占比最多,这是因为每次挖空都需要解数独来判断是否是唯一解,在这里暂时没有什么好的解决方法。
7. 看Design by Contract, Code Contract的内容:描述这些做法的优缺点, 说明你是如何把它们融入结对作业中
CodeContract即代码契约,就是要两个人约定函数,类的接口设计,并说明注意事项,例如:
- 可以接受和不可接受的参数类型以及取值范围,以及它们的意义
- 返回值的范围和类型及其意义
- 可能出现的异常和错误以及其意义
- 函数的副作用,比如改变了什么指针的值
- 函数使用的先决条件是什么
- 等等
这样约定接口设计的优点在于,函数调用者使用的时候不需要考虑函数的具体实现就能够根据其用法说明来顺利地调用(当然前提是这个函数写对了),缺点在于按这种方式编程在过程中会比较繁琐,对于一些功能简单的函数也这么写的话会显得杂乱(有的函数一看函数名就能够了解它的意思了),在实际的结对编程中,我们简化了维基百科上的要求,在比较复杂的函数之前加了注释告诉调用者函数做了什么,返回值是什么,接受参数等等,对于比较简单简短的函数则省略这一过程。
8. 计算模块部分单元测试展示
首先是命令行参数的单元测试,例如:
TEST_METHOD(TestMethod5) { // -r 23~29 -u -n 124 int argc = 6; char *argv[] = { "sudoku.exe", "-r", "23~29", "-u" ,"-n","124" }; ArgumentHandler ah; ah.ParseInput(argc, argv); bool r = ah.GetCount() == 124 & ah.GetState() == State::GEG_RU& ah.GetLower() == 23 & ah.GetUpper() == 29 & ah.GetPathName() == NULL& ah.GetDifficulty() == Difficulty::UNS; Assert::AreEqual(r, true); }
这样测试ArgumentHandler是否能完成参数分析的工作,上面的这个测试用例将参数输入的顺序打乱,还有一系列的参数输入都与之类似,这里就不放代码了;
接下去是对于Core中solve函数的正确性测试,例如:
// test API generetor TEST_METHOD(TestMethod11) { int p[9][9] = { { 0,0,0,0,0,0,8,0,0 }, { 0,1,0,2,3,5,4,0,0 }, { 0,0,9,0,6,0,0,5,3 }, { 0,6,0,3,0,0,0,4,0 }, { 0,9,5,0,8,0,1,3,0 }, { 0,7,0,0,0,2,0,8,0 }, { 9,5,0,0,2,0,3,0,0 }, { 0,0,3,1,7,6,0,9,0 }, { 0,0,7,0,0,0,0,0,0 } }; int puzzle[81]; Transform(p, puzzle); int solution[81]; bool r = solve(puzzle, solution); r &= IsTrueAnswer(puzzle, solution); r &= IsValid(solution); Assert::AreEqual(r, true); }
给出一个数独题,解之,判断其是否是有效的解;
之后是对于API中generate函数的测试,主要是对生成的数独终局的判重和生成的数独题目的判重和唯一解性的测试:
TEST_METHOD(TestMethod13) { int size = 1000; int(*result)[81] = new int[size][81]; generate(size, result); bool r = IsDiffer(result, size); for (int i = 0; i < size; i++) r &= IsValid(result[i]); delete[] result; Assert::AreEqual(r, true); } TEST_METHOD(Test14) { // -n 100 -r 23~29 int size = 1000; int(*result)[81] = new int[size][81]; generate(size, 23, 29, false, result); bool r = IsInRange(23, 29, result, size); int solution[81]; for (int i = 0; i < size; i++) { r &= solve(result[i], solution); r &= IsValid(solution); } Assert::AreEqual(r, true); }
上面测试生成数独终局的判重和生成随机挖空数独的测试,下面是生成唯一解数独的测试:
TEST_METHOD(Test15) { // -n 100 -r 40~50 -u int size = 100; int(*result)[81] = new int[size][81]; generate(size, 40, 50, true, result); bool r = IsInRange(40, 50, result, size); int solution[81]; for (int i = 0; i < size; i++) { r &= solve(result[i], solution); r &= IsValid(solution); } Table table; for (int k = 0; k < size; k++) { for (int i = 0; i < 81; i++) { table.cells[i / 9][i % 9] = result[k][i]; } r &= table.startSolving(2, NULL) == 1; } Assert::AreEqual(r, true); }
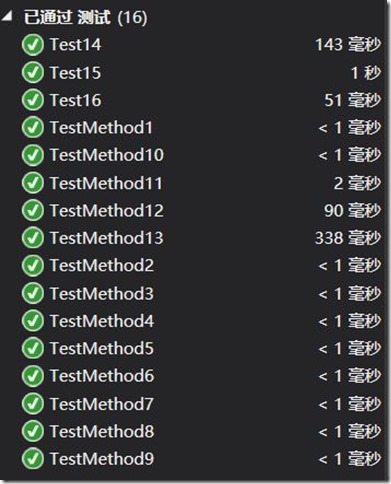
下面是单元测试运行的结果和代码覆盖率:
9. 计算模块部分异常处理说明
异常处理模块分两部分,一部分在ArgumentHandler之中对命令行参数进行判断,我这里设置了18种不同的异常,下面给出参数分析函数(其中进行了异常处理):
void ArgumentHandler::ParseInput(int argc, char** args) { if (argc < 3) { cout << "The number of arguments is not correct!" << endl; return; } if (strcmp(args[1], "-c") == 0) { state = State::GEN; try { if (argc != 3) { throw invalid_argument("Argument "-c" shouldn't be used with other arguments!"); } else if (!IsDigit(args[2])) { throw invalid_argument("The argument of "-c" should be a positive integer!"); } sscanf_s(args[2], "%d", &count); if (count > maxCounts||count<=0) { throw invalid_argument("The argument of "-c" should be in range [1,1000000]!"); } } catch (invalid_argument err) { state = State::INV; cout << err.what() << endl; } } else if (strcmp(args[1], "-s") == 0) { state = State::SOV; try { if (argc != 3) { throw invalid_argument("Argument "-s" shouldn't be used with other arguments!"); } pathname = args[2]; } catch (invalid_argument err) { state = State::INV; cout << err.what() << endl; } } else { state = GEG_M; int nUsed = 0; int mUsed = 0; int rUsed = 0; int uUsed = 0; for (int i = 1; i < argc; ++i) { if (strcmp(args[i], "-n") == 0) { nUsed++; try { if (i + 1 == argc) { throw invalid_argument("Required argument of "-n" missing!"); } if (!IsDigit(args[i + 1])) { throw invalid_argument("The argument of "-n" should be a positive integer!"); } sscanf_s(args[i + 1], "%d", &count); if (count > maxN||count<=0)//test int.max+1 { throw invalid_argument("The argument of "-n" should be in range [1,10000]!"); } i++; } catch (invalid_argument err) { cout << err.what() << endl; state = State::INV; break; } } else if (strcmp(args[i], "-m") == 0) { mUsed++; try { if (i + 1 == argc) { throw invalid_argument("Required argument of "-m" missing!"); } if (args[i+1][1]!='�') { throw invalid_argument("The argument of "-m" should be only a digit!"); } switch (args[i + 1][0]) { case '1': difc = Difficulty::EASY; break; case '2': difc = Difficulty::NORMAL; break; case '3': difc = Difficulty::HARD; break; default: throw invalid_argument("The argument of "-m" should be only 1, 2 or 3!"); break; } i++; } catch (invalid_argument err) { cout << err.what() << endl; state = State::INV; break; } } else if (strcmp(args[i], "-u") == 0) { uUsed++; unique = true; } else if (strcmp(args[i], "-r") == 0) { rUsed++; try { if (i + 1 == argc) { throw invalid_argument("Required argument of "-r" missing!"); } if (!JudgeR(args[i + 1]) || (sscanf_s(args[i + 1], "%d~%d", &lower, &upper) != 2)) { throw invalid_argument("The argument of "-r" should be in format: lower~upper, and lower/upper must be a positive integer!"); } if (lower < minR || lower > maxR || upper < minR || upper > maxR || lower > upper) { throw invalid_argument("The two arguments of "-r" should be in range [20, 55] , and the first number must be no more than the second number!"); } i++; } catch (invalid_argument err) { cout << err.what() << endl; state = State::INV; break; } } else { state = State::INV; cout << "We only support the arguments as follows: -c, -s, -n, -r, -m, -u! And -c/-s can only be used alone!" << endl; break; } } if (state == State::GEG_M) { if (nUsed > 1 || uUsed > 1 || mUsed > 1 || rUsed > 1) { cout << "Every argument should be used only once!" << endl; state = State::INV; } else if (mUsed&rUsed || mUsed&uUsed) { cout << "Argument -m shouldn't be used with -r or -u!" << endl; state = State::INV; } else if (!nUsed || (nUsed & !mUsed & !rUsed & !uUsed)) { cout << "Argument -n must be used at least once, and it should be used together with -m/-r/-u!" << endl; state = State::INV; } else if(rUsed>0 && uUsed>0) { state = GEG_RU; } else if (rUsed > 0) { state = GEG_R; } else if (uUsed > 0) { state = GEG_U; } } } }
具体的异常类型在上面的代码中可以很好的看出来,因为每个异常的具体说明都是对用户的错误提示,在catch块中进行了输出,之后设置程序运行模式为INV(invalid),在退出参数处理模块后,main函数就会自动退出。
另一个异常处理在Core模块中,当用户调用动态链接库的输出函数时使用了不恰当的参数的时候,应该有Core模块抛出异常,下面以Core模块中的其中一个generate的重载来说明这里面的异常处理:
void generate(int number, int lower, int upper, bool unique, int result[][81]) { if (number < 0) { throw invalid_argument("The argument of "-n" shouldn`t be less than zero"); } else if (number > gMaxGenRanAmount) { throw invalid_argument("The argument of "-n" shouldn`t be bigger than 10000"); } else if (lower < gGenRangeLower || lower >gGenRangeUpper || upper < gGenRangeLower || upper >gGenRangeUpper) { throw invalid_argument("The argument of "-r" should be in the range of [20,55]"); } else if (lower > upper) { throw invalid_argument("The argument of "-r" should be like lower~upper."); } else if (result == NULL) { throw invalid_argument("The argument of result shouldn`t be NULL"); } ////////////////////////////后面省略 }
在这里面,我们判断了输入的number是不是在1-10000之间,以及lower和upper是否满足20-55的要求,以及result这样一个用于输出的二维数组是否是无效的。其他几个API接口函数都类似这样进行了处理。
10. 界面模块的详细设计过程
在界面模块方面,我们可能用了比较冷门的技术…小伙伴蔡帜同学向我安利了Cocos2dx,这是一个2D游戏引擎(因为他觉得Qt太丑了),他以前用这个引擎写过东西,但是由于种种原因,最后是我这个什么都不会的人写的GUI,于是上演了一周速成cocos的戏码……使用的版本是cocos2dx 3.15,原生态纯C++导入到VS进行编写。
我们首先讨论设计了UI的大致结构,这一部分内容可以移步我的github项目里的DesignUIStructure.txt中查看,一个很粗略的设计,在设计之前我看了两整天的有关cocos的技术博客,之前还花了半天时间配环境,所以时间很紧迫。界面模块主要由三个场景(Scene)组成:
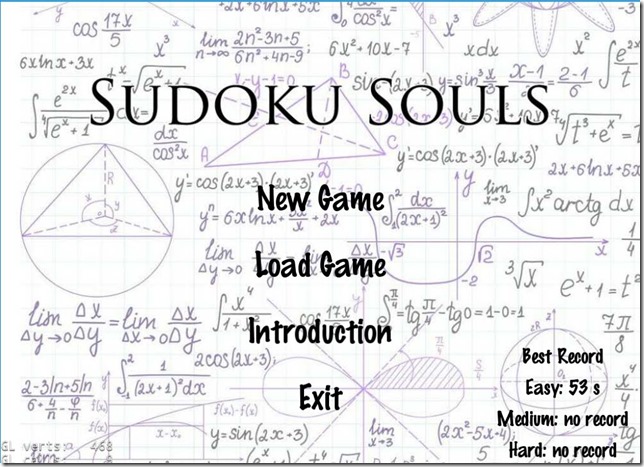
1. 开始界面,包含菜单栏,以及显示当前各个难度最佳记录
点击NewGame将会弹出对话框让你选择难度,当然也有取消按钮,选择难度后进入游戏场景;
点击LoadGame将会载入上一次保存的存档,并进入游戏场景继续上一次的游戏;
点击Introduction将会进入游戏介绍,包含规则介绍和方法介绍;
右下角为显示的当前最佳记录;点击Exit退出游戏;
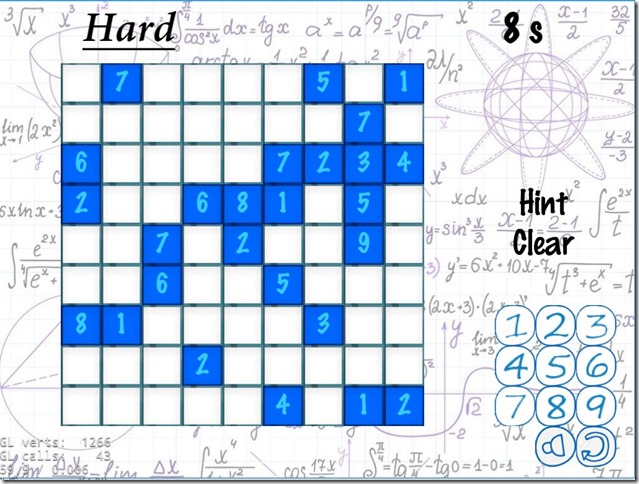
2. 游戏界面
可以看到左上角显示当前难度,右上角为计时,网格右边为提示和清空按钮;
点击Hint将会在当前选择的格子处给出填数的提示;
点击Clear将清空所有已填数字(当你混乱的时候可以使用);
右下角是9个填数按钮,点击后将在当前选择的格子处填上相应数字;
点击右下角喇叭按钮,将关闭背景音乐,同时样子变成第二个图的样子;
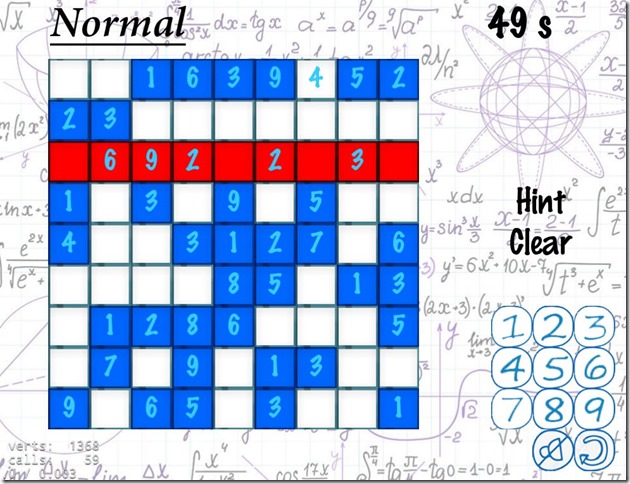
在游戏界面为了提高用户体验,我们有自动检错功能,如图二;
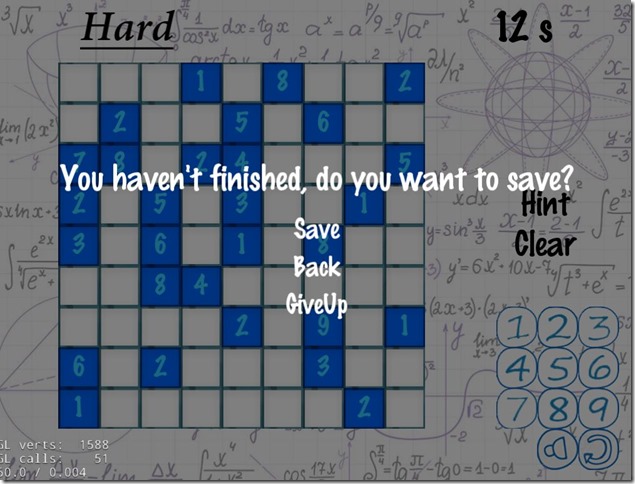
点击右下角返回按钮,将弹出对话框询问是否保存,同时有返回游戏按钮和放弃按钮,如图三;
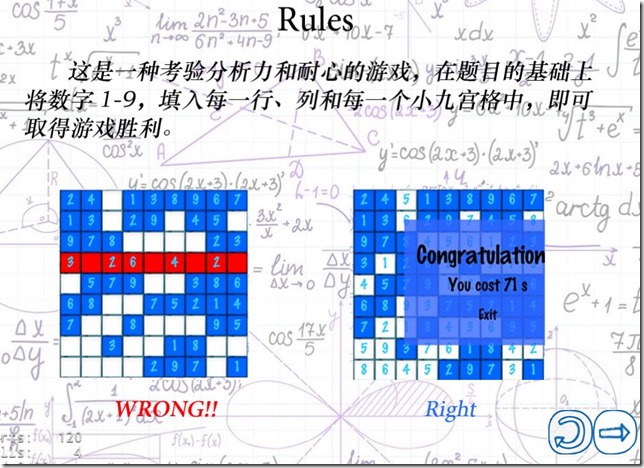
3.介绍界面
介绍的第一张图给出了规则和对应的游戏截图,点击右下角返回按钮返回开始界面;
点击右箭头将会进入下一张介绍,点击左箭头返回上一张(这里的界面切换用的滑动,以配合箭头的设计);
在任何一张介绍中用户都能返回主菜单;
本次UI是我从零开始学习并编写的,上面的游戏中使用的素材(棋盘,背景,介绍文字和图片,按钮)是小伙伴花了六七个小时P出来的。
下面以游戏场景的部分代码(github中UISourceCode目录下)为例介绍部分实现过程:
void GameScene::NumbutCallBack(Ref* pSender, Control::EventType type) { if (selected != -1 && !ShareGlobal()->grid[selected / 9][selected % 9].isGiven) { int i; for (i = 0; i < 9; i++) { ControlButton* t = (ControlButton*)this->getChildByTag(300 + i); if (t == pSender) break; } Label* grid = (Label*)this->getChildByTag(100 + selected); grid->setString(std::string(1, char('0' + i + 1))); ShareGlobal()->grid[selected / 9][selected % 9].num = i + 1; // 若上次改变了颜色,则恢复之 if (lastCheck != -1) { if (lastCheck < 9) { // 行恢复 for (int i = 0; i < 9; i++) { Sprite* s = (Sprite*)this->getChildByTag(200 + 9 * lastCheck + i); int isGiven = ShareGlobal()->grid[lastCheck][i].isGiven; if (isGiven) s->setColor(Color3B(0, 102, 255)); else s->setColor(Color3B(255, 255, 255)); } // 恢复后重置lastcheck lastCheck = -1; } else if (lastCheck < 19) { // 列恢复 lastCheck -= 10; for (int i = 0; i < 9; i++) { Sprite* s = (Sprite*)this->getChildByTag(200 + 9 * i + lastCheck); int isGiven = ShareGlobal()->grid[i][lastCheck].isGiven; if (isGiven) s->setColor(Color3B(0, 102, 255)); else s->setColor(Color3B(255, 255, 255)); } // 恢复后重置lastcheck lastCheck = -1; } else { // 宫恢复 lastCheck -= 20; int rs = 3 * (lastCheck / 3); int cs = 3 * (lastCheck % 3); for (int i = rs; i < rs + 3; i++) { for (int j = cs; j < cs + 3; j++) { Sprite* s = (Sprite*)this->getChildByTag(200 + 9 * i + j); int isGiven = ShareGlobal()->grid[i][j].isGiven; if (isGiven) s->setColor(Color3B(0, 102, 255)); else s->setColor(Color3B(255, 255, 255)); } } // 恢复后重置lastcheck lastCheck = -1; } } // 检测是否又不符合数独规则的行列宫,改变相应子结构的颜色 // 只改变第一个发现的子结构,待用户解决后,才会提示另外的错误 int line = ShareGlobal()->CheckLine(); int column = ShareGlobal()->CheckColumn(); int cell = ShareGlobal()->CheckCell(); if (line != -1) { for (int i = 0; i < 9; i++) { Sprite* s = (Sprite*)this->getChildByTag(200 + 9 * line + i); s->setColor(Color3B(255, 0, 0)); } lastCheck = line; } else if (column != -1) { for (int i = 0; i < 9; i++) { Sprite* s = (Sprite*)this->getChildByTag(200 + 9 * i + column); s->setColor(Color3B(255, 0, 0)); } lastCheck = 10 + column; } else if (cell != -1) { int rs = 3 * (cell / 3); int cs = 3 * (cell % 3); for (int i = rs; i < rs + 3; i++) { for (int j = cs; j < cs + 3; j++) { Sprite* s = (Sprite*)this->getChildByTag(200 + 9 * i + j); s->setColor(Color3B(255, 0, 0)); } } lastCheck = 20 + cell; } // 如果上面的没有问题并且用户填完了,弹出对话框示意结束 else if (ShareGlobal()->IsFinished()) { // 获取屏幕宽度和高度 auto visibleSize = Director::getInstance()->getVisibleSize(); Vec2 origin = Director::getInstance()->getVisibleOrigin(); // 设置对话框颜色,位置,透明度 Director::getInstance()->getEventDispatcher()->pauseEventListenersForTarget(this, true); auto colorLay = LayerColor::create(Color4B(51, 102, 255, 200)); colorLay->ignoreAnchorPointForPosition(false); colorLay->setAnchorPoint(Vec2(0.5, 0.5)); colorLay->changeHeight(visibleSize.height / 2); colorLay->changeWidth(visibleSize.width / 2); colorLay->setPosition(Vec2(origin.x + visibleSize.width / 2, origin.y + visibleSize.height / 2)); this->addChild(colorLay, 3); // 显示文本 auto label = Label::createWithTTF("Congratulations!", "fonts/Marker Felt.ttf", 70); label->setPosition(Vec2(origin.x + visibleSize.width / 4, origin.y + visibleSize.height / 4+80)); label->setColor(Color3B(0, 0, 0)); colorLay->addChild(label, 4); // 用时 std::string stime("You cost "); char ctime[6]; itoa(time, ctime, 10); stime += ctime; stime += " s"; auto tlabel = Label::createWithTTF(stime.c_str(), "fonts/Marker Felt.ttf", 50); tlabel->setPosition(Vec2(origin.x + visibleSize.width / 4, origin.y + visibleSize.height / 4 -10)); tlabel->setColor(Color3B(0, 0, 0)); colorLay->addChild(tlabel, 4); // 记录最佳时间 if (ShareGlobal()->degree == 1 && (ShareGlobal()->bestRecordEasy > time || ShareGlobal()->bestRecordEasy == -1)) { // 如果没有记录或是好于最佳记录 CCUserDefault::sharedUserDefault()->setIntegerForKey("bestRecordEasy", time); } if (ShareGlobal()->degree == 2 && (ShareGlobal()->bestRecordMedium > time || ShareGlobal()->bestRecordMedium == -1)) { // 如果没有记录或是好于最佳记录 CCUserDefault::sharedUserDefault()->setIntegerForKey("bestRecordMedium", time); } if (ShareGlobal()->degree == 3 && (ShareGlobal()->bestRecordHard > time || ShareGlobal()->bestRecordHard == -1)) { // 如果没有记录或是好于最佳记录 CCUserDefault::sharedUserDefault()->setIntegerForKey("bestRecordHard", time); } // 返回主菜单的按钮 auto closeLabel = Label::createWithTTF("Exit", "fonts/Marker Felt.ttf", 40); closeLabel->setColor(Color3B(0, 0, 0)); auto closeItem = MenuItemLabel::create(closeLabel, [=](Ref* pSender) {// 销毁图层,恢复监听,返回主菜单 colorLay->removeFromParent(); Director::getInstance()->getEventDispatcher()->resumeEventListenersForTarget(this, true); auto scene = HelloWorld::createScene(); Director::getInstance()->replaceScene(TransitionCrossFade::create(0.4, scene)); }); closeItem->setPosition(Vec2(origin.x + visibleSize.width / 4, origin.y + visibleSize.height / 4 - 100)); auto menu = Menu::create(closeItem, NULL); menu->setPosition(Vec2::ZERO); colorLay->addChild(menu, 5); } } }
这是游戏界面中最核心的填数代码,即右下角9个迷你键盘的回调函数,包含每次填数的自动检测:
每次填数时都会首先将上次填数时造成的颜色变换(填数错误的红色,以及选择格子的颜色变化),这里上次的错误提示位置我用lastCheck这个类私有变量来记录;
然后利用层内ControlButton对象的Tag判断点击的数字,在当前选择的空格(selected进行记录)上填入该数字,判断是否有填数错误,如果有的话将错误的那一行/列/宫涂红;
若没有错误则判断是否填的是最后一个格子,是的话显示对话框,打印出”Congratulations”字样,告诉用户完成时间,并自动刷新最佳记录,同时给出返回按钮,直接使用lambda函数定义其回调函数为销毁该对话框的图层,恢复下方图层的事件监听并返回主菜单界面;
static Global* m_global = NULL; Global* ShareGlobal() { if (m_global == NULL) { m_global = new Global(); } return m_global; }
class Global { public: Global(); ~Global(); typedef struct table { int num; bool isGiven; }Table; Table grid[9][9]; bool Check(); bool IsFinished(); int degree; void GenerateGame(); // 返回 -1 表示没有发现错误,返回 0-8 表示某行列宫存在错误 int CheckLine(); int CheckColumn(); int CheckCell(); // 初始化时记录时间 int time; // 最佳记录 int bestRecordEasy; int bestRecordMedium; int bestRecordHard; // 生成当前数独的解,用于提示功能 void GenerateSolution(); int solution[9][9]; };
对于一些所有界面都可能需要用到的参数,我设置了一个Global类来进行保存,设置一个Global类的静态变量m_global供各个界面引用与修改,具体定义请看上面的代码,例如上面的代码中使用Global类的函数ShareGlobal()调用其返回的类对象的成员函数check和isfinished来判断填数错误和完成度,此外鼠标点击的填数动作也会改变该全局变量的grid,在保存的时候只需要将grid保存成字符串即可,而在下次Load旧游戏的时候就只需要重新初始化m_global就可以了,global类的成员在上面有清晰的注释,不难理解,都是需要在屏幕上显示的或是游戏过程中需要使用的元素。
11. 界面模块与计算模块的对接
界面模块主要使用了上面的core模块的两个函数,一个是生成指定难度的数独题目,另一个是解数独的程序,用于进行提示。这两个函数的调用我都放在上面提高的Global类中进行,下面是相关代码:
void Global::GenerateGame() { int result[1][81]; generate(1, degree, result); for (int i = 0; i < 81; i++) { grid[i / 9][i % 9].num = result[0][i]; grid[i / 9][i % 9].isGiven = result[0][i] != 0 ? true : false; } } void Global::GenerateSolution() { int puzzle[81]; int result[81]; for (int i = 0; i < 81; i++) { puzzle[i] = grid[i / 9][i % 9].num; } solve(puzzle, result); for (int i = 0; i < 81; i++) { solution[i / 9][i % 9] = result[i]; } }
Global类中的grid保存生成的数独题目和格子是不是已填的(数独题的已知格子),这样在读取存档的时候也能知道哪些格子是用户填的,类成员solution保存当前的数独题目的解,这两个函数是在进入游戏界面时就会调用的,在退出时将会保存当前的grid,在下次读取存档时将存档中的grid读下来放进grid,再次调用solve生成解。实现的功能就是提示和生成数独,这样实现的游戏功能截图见上面的分析,提示功能请自行体验:D
12. 描述结对的过程,提供非摆拍的两人在讨论的结对照片
上课选结对伙伴的时候我们俩都没找到,互相看见了就结对了…结对过程还算顺利吧,各自完成约定的工作,就是中间有的时候会有点拖,导致最后时间有点紧,中间一直在新主楼讨论问题,下面是我拍的一张小伙伴敲代码的照片:
本次作业的分工大致是我做了GUI,两个人一起讨论Core的实现,我完成了其中的参数处理模块和难度评估模块,搭档完成了其他模块的改进和拼接。
13. 说明结对编程的优点和缺点
优点:
- 思路比较清晰,两个人一起讨论一起写代码,出现的问题会少一点
- Debug过程会比较顺畅,两个人一起可以很快定位BUG所在的位置
- 互相学习对方写代码的优点和改正双方的缺点
缺点:
- 需要同步双方的进度,速度快的一方体验会差
- 一些小问题常常纠结不下,实际上一个人写很快就解决了
- 拖延症什么的……
14. 在你实现完程序之后,在附录提供的PSP表格记录下你在程序的各个模块上实际花费的时间
见2
15. 感想
虽然没有要求写感想但是我还是习惯性写了……首先这次作业其实完成的不是很从容,后期由于种种原因比较拖,之后的测试感觉上去可能会比较崩,因为我们的算法比较繁琐,特别是生成指定难度的数独,因为没有考虑常规思路而是实现了许多解数独的策略来让计算机尝试,生成下来可能会比较慢,比如生成10000个高难度数独就会远超1min,但是我在写GUI调用我们的core的时候其实只用生成一个就好了…实际上我们实现的时候由参考文中提到的SudokuExplainer这个软件,它号称解所有的数独都不需要猜,我们看了里面对于数独难度的划分就是按照策略的不同来划分的,当然这个软件实现了几乎所有的解数独策略,用这个软件生成一个较难的数独实际上比我的GUI生成一个数独慢呢,想来也是这么试出来的吧……最后其实我是国庆结束后的周日才开始从零开始学的cocos,能在一周时间内写出来一个能看的游戏我其实已经很满意了,成绩什么的就那样吧~~~
PS:课上好像说要加对小伙伴的建议,我只想说,拖延症该改改了~~