树、二叉树、查找算法总结

思维导图

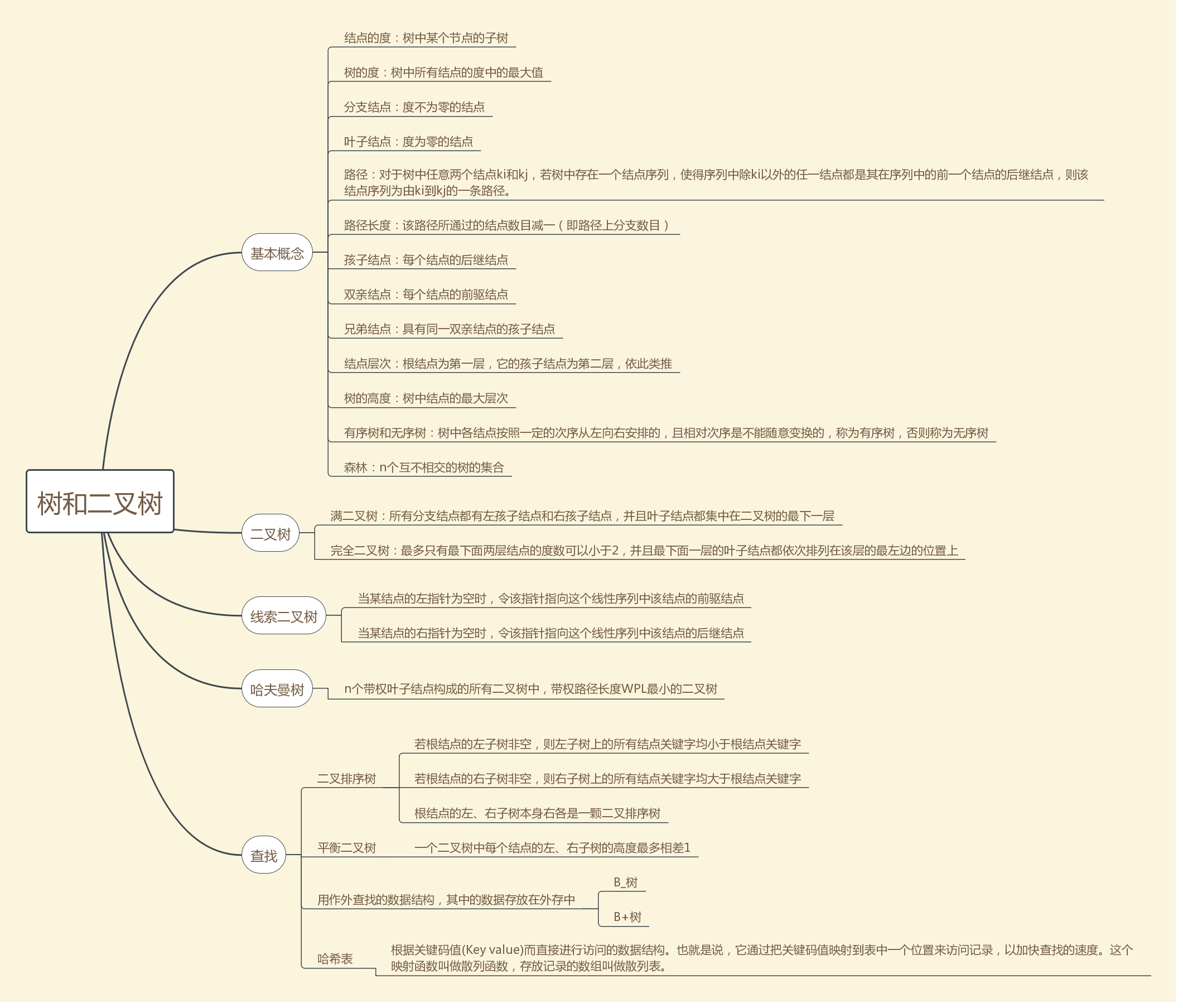
重要概念

二叉树的性质

1. 非空二叉树上的叶子结点数等于双分支结点数加1
2. 非空二叉树的第i层上最多有2^(i-1)个结点(i>=1)
3. 高度为h的二叉树最多有2^h - 1个结点(h>=1)
4. 具有n个(n>0)结点的完全二叉树的高度为

[ lceil log_{2}{(n+1)} ceil ]

或

[ lfloor log_{2}{n} floor +1 ]

查找

1. 若整个查找过程都在内存中进行，则称之为内查找；反之，若查找过程需要访问外存，则称之为外查找。
2. 若在查找的同时对表做修改操作（如插入和删除），则相应的查找表称为动态查找表。若在查找中不涉及表的修改操作，则相应的查找表称为静态查找表。
3. 在查找运算中时间主要花费在关键字的比较上，把平均需要和给定值k进行比较的关键字次数称为平均查找长度（ASL）。

线性表的查找

1. 顺序查找：比较简单
2. 折半查找：又称二分查找，它是一种效率较高的查找方法。但是，折半查找要求线性表是有序表，即表中的元素按关键字有序。

哈希表查找性能

1. 与装填因子α有关。所谓装填因子是指哈希表中已存入元素数n与哈希地址空间大小m的比值，即α=n/m。α越小，冲突的可能性越小；相反，则更大。
2. 与所采用的哈希函数有关。若哈希函数选择得当，就可以使哈希地址尽可能均匀地分布在哈希地址空间上，从而减少冲突的发生；否则，若哈希函数选择不当，就可能使哈希地址集中于某些区域，从而加大冲突的发生。
3. 当出现哈希冲突时需要采取解决哈希冲突的方法，所以哈希查找性能也与解决冲突的方法有关。

哈希表的构造方法

1. 直接定址法
2. 除留余数法
3. 数字分析法

哈希冲突解决方法

1. 开放定址法：出现哈希冲突时在哈希表中找到一个新的空闲位置存放元素。
   1. 线性探测法
   2. 平方探测法
2. 拉链法：把所有的同义词用单链表链接起来的方法。
   与开放定址法相比，拉链法有以下几个优点：
   1. 拉链法处理冲突简单，且无堆积现象，即非同义词绝不会发生生冲突，因此平均查找长度较短；
   2. 由于拉链法中各单链表上的结点空间是动态申请的，故它更适合于造表前无法确定表长的情况；
   3. 开放定址法为减少冲突要求装填因子α较小，故当数据规模较大时会浪费很多空间，而拉链法中可取α>=1，且元素较大时拉链法中增加的指针域可忽略不计，因此节省空间；
   4. 在用拉链法构造的哈希表中，删除结点的操作更加易于实现。

拉链法也有缺点：指针需要额外的空间，故当元素规模较小时开放定址法较为节省空间，若将节省的指针空间用来扩大哈希表的规模，可使装填因子变小，这又减少了开放定址法中的冲突，从而提高了平均查找速度。

疑难问题及解决方案

刚开始一直想着怎么从u和v往上找，u和v又只有孩子指针，没法往上找。后来从二叉搜索树的性质入手，解决了问题。
对于某一个结点p，如果u->key < p->key 并且 v->key > p->key，则这个结点即为最近公共祖先。如果u和v都在p的左子树或右子树，则继续往相对应的左子树或右子树查找，直到符合u->key < p->key 并且 v->key > p->key为止。

int Find(Tree T,int x)
{
    if (!T) return 0;
    if (T->Key == x)
    {
        return 1;
    }
    if (x > T->Key)
    {
        return Find(T->Right, x);
    }
    if (x < T->Key)
    {
        return Find(T->Left, x);
    }
}
int LCA( Tree T, int u, int v )
{
    if (!T)
    {
        return ERROR;
    }
    if (!Find(T, u) || !Find(T, v))
    {
        return ERROR;
    }else if (u == v)
    {
        return u;
    }
    if (u > T->Key && v > T->Key)
    {
        return LCA(T->Right, u, v);
    }
    if (u < T->Key && v < T->Key)
    {
        return LCA(T->Left, u, v);
    }
    if ( (u > T->Key && v < T->Key) || (u < T->Key && v > T->Key) )
    {
        return T->Key;
    }
}