836：矩形重叠（C++）

题目地址：https://leetcode-cn.com/problems/rectangle-overlap/

题目描述

矩形以列表 [x1, y1, x2, y2] 的形式表示，其中 (x1, y1) 为左下角的坐标，(x2, y2) 是右上角的坐标。如果相交的面积为正，则称两矩形重叠。需要明确的是，只在角或边接触的两个矩形不构成重叠。给出两个矩形，判断它们是否重叠并返回结果。

题目示例

示例 1：

输入：rec1 = [0,0,2,2], rec2 = [1,1,3,3]
输出：true

示例 2：

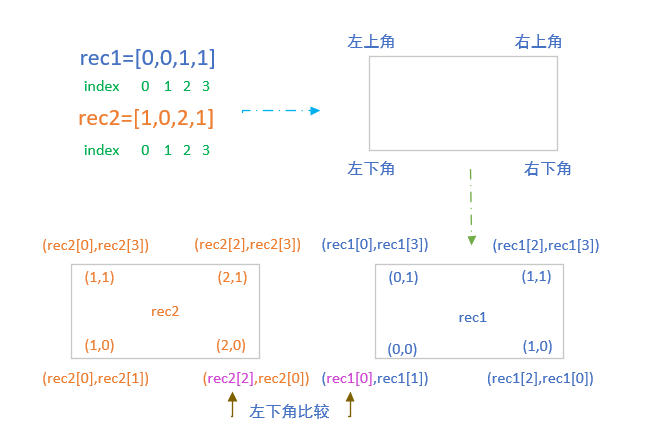
输入：rec1 = [0,0,1,1], rec2 = [1,0,2,1]
输出：false

说明：两个矩形 rec1 和 rec2 都以含有四个整数的列表的形式给出；矩形中的所有坐标都处于 -10^9 和 10^9 之间。

解题思路

位置判断法：我们利用反向思考的方法，思考什么条件下两个矩形不会重叠，即不产生矩阵重建的条件是什么？然后对不满足重叠的条件取反，即可得到重叠。通过画图，可以很容易发现，不产生重叠的位置总共有四个，分别是上侧、下侧、左侧和右侧。为了便于理解，我用下面图例来阐述，比较发现当满足以下几个条件时，不产生重叠，即

• rec1[2] <= rec2[0]  //矩形rec1右侧无重叠

• rec2[3] <= rec1[1]  //矩形rec1下侧无重叠

• rec1[3] <= rec2[1]  //矩形rec1上侧无重叠

• rec2[2] <= rec1[0]  // 矩形rec1左侧无重叠

投影法：从数学角度来看，矩形重叠会产生重叠区域，那么，重叠区域可以用投影线段来衡量，在水平方向上的投影矩阵rec1是(rec1[0]，rec1[2])，而矩阵rec2是(rec2[0]，rec2[2])，竖直方向的投影两个矩阵rec1和rec2分别是(rec1[1]，rec1[3])和(rec2[1]，rec2[3])。我们发现，当水平方向上满足min(rec1[2]，rec2[2]) > max(rec1[0]，rec2[0])时，产生水平交集，同样的，当竖直方向上满足min(rec1[3]，rec2[3]) > max(rec1[1]，rec2[1])时，产生竖直交集。

程序源码

class Solution {
public:
    bool isRectangleOverlap(vector<int>& rec1, vector<int>& rec2) {
        // 位置法
        return !(rec1[2] <= rec2[0] || //右侧
                 rec2[3] <= rec1[1] || //下侧
                 rec1[3] <= rec2[1] || //上侧
                 rec2[2] <= rec1[0]);  //左侧
        /* 投影法
         return (min(rec1[2], rec2[2]) > max(rec1[0], rec2[0]) &&
                 min(rec1[3], rec2[3]) > max(rec1[1], rec2[1]));
        */
    }
};