绵阳东辰国际test201910.21

爆零警告，昨天晚上睡得晚，考试的时候困死我了

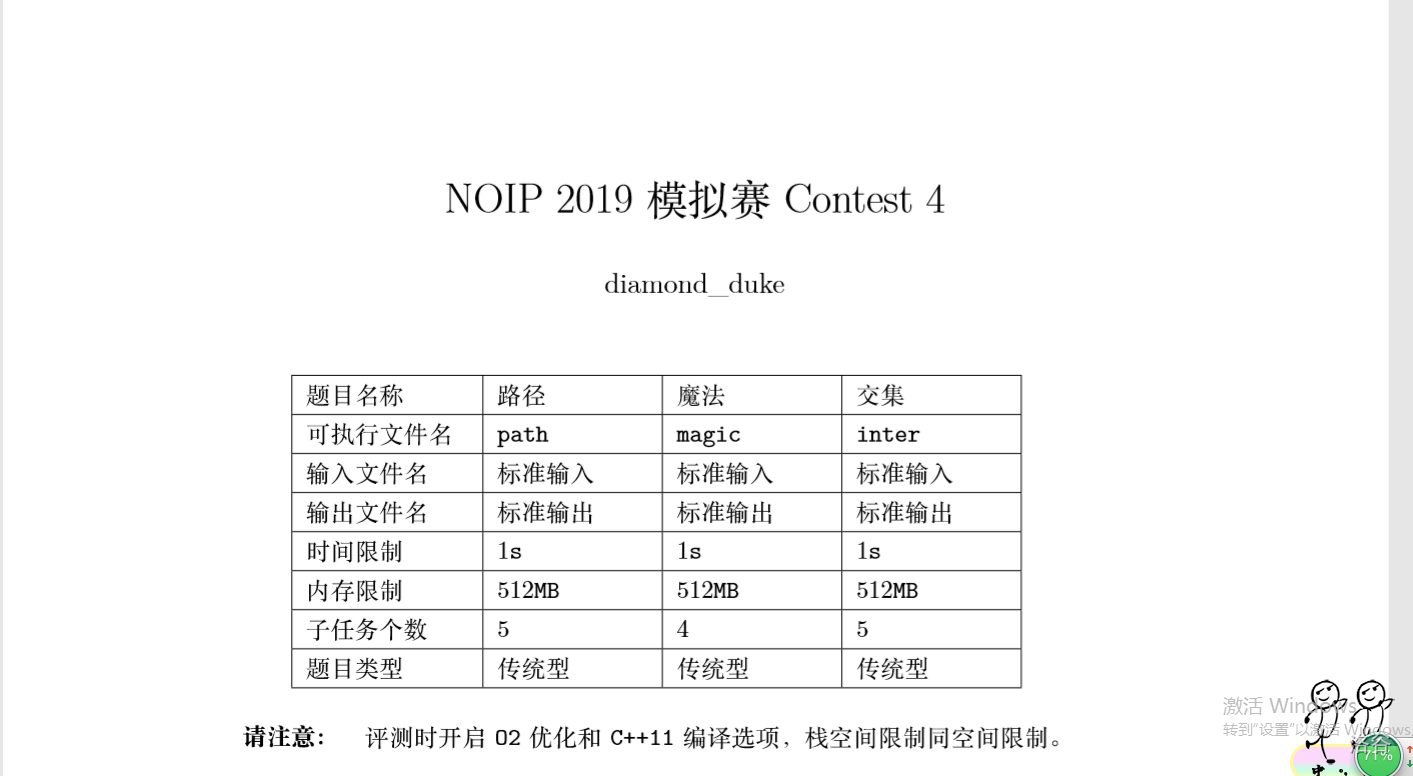
分析：

哈密尔顿环：每个点只经过一次的路线，有哈密尔顿环的图叫哈密尔顿图

先考虑只是一条链

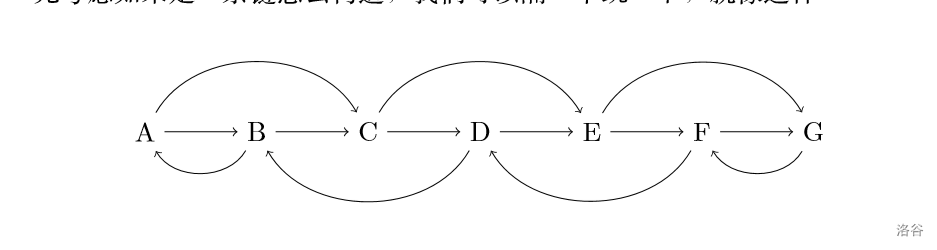
很容易想到隔一个跳一次，这样无论链有多长一定是从A出发，B回来

所以直接拓展到树上即可：

如 果当前节点深度是奇数，那么我们在DFS前输出这个点，

否则在DFS完所有孩子之 后再输出这个点。

part code：

il void dfs(int u,int fa){
      dp[u]=dp[fa]+1;
      if(dp[u]&1){printf("%d
",u);}
      for(ri i=head[u];i;i=edg[i].next){
      int to=edg[i].to;
      if(to==fa)continue;
      dfs(to,u);
      }
      if(!(dp[u]&1)){printf("%d
",u);}
}

什么跳两次的滚出

总结：有很多的dfs题代码很简单，却很容易陷阱去，导致思路开花，应该往简单的方向想

不禁想到一句诗：众里寻他千百度，那人却在灯火阑珊处

分析：

首先用kmp或者哈希对每个 Ti，求出它在 S 中的匹配位置

那么这些位置 中至少得要删掉一个

考虑如果两个区间的R相等时，这时就只用管L最大的

证明

为什么因为先满足L较大的，其他的同R的肯定都满足了

而先满足L较小的，L较大的不一定满足，所以这样一定是最优的

于是对于每个 i，我们可以求出一个 Li

如果没有的直接从前面dp转移过来就可以

然后很明显就要dp了

设dp[i]前i个位置都满足，且最后一个删的是i的最小值

Li是单调递增的

所以维护单调递增队列dp

code by CHiTongZi

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
char S[N], T[N];
int n, m, a[N], d[N];
inline void calc ()
{
	static int nxt[N];
	int cur = 0, len = strlen (T + 1);
	for (int i = 2; i <= len; ++i)
	{
		while (cur && T[cur + 1] != T[i]) cur = nxt[cur];
		nxt[i] = cur + (T[cur + 1] == T[i]);
		cur += T[cur + 1] == T[i];
	}

	cur = 0;
	for (int i = 1; i <= n; ++i)
	{
		while (cur && T[cur + 1] != S[i]) cur = nxt[cur];
		if (T[cur + 1] == S[i]) cur++;
		if (cur == len) d[i] = max (d[i], i - len + 1), cur = nxt[cur];
	}
}
int q[N], p[N], dp[N], tail = 1, head = 1;
inline void insert (int vv, int k)
{
	while (tail >= head && q[tail] >= k) tail--;
	q[++tail] = k;
	p[tail] = vv;
}
inline int query (int lp)
{
	while (tail >= head && p[head] < lp) head++;
	return q[head];
}
int main ()
{
	memset (d, -1, sizeof d);
	scanf ("%d%d", &n, &m);
	scanf ("%s", S + 1);
	for (int i = 1; i <= n; ++i)scanf ("%d", &a[i]);
	for (int i = 1; i <= m; ++i)scanf ("%s", T + 1), calc();
	int rpoint = -1;
	for (int i = 1; i <= n ; ++i)
	{
		if (rpoint >= d[i])d[i] = -1;
		rpoint = max (rpoint, d[i]);
	}
	for (int i = 1; i <= n; ++i)
	{
		insert (i, a[i] + dp[i - 1]);
		if (d[i] == -1) dp[i] = dp[i - 1];
		else dp[i] = query (d[i]);
	}
	printf ("%d
", dp[n]);
	return 0;
}

分析：
问题转化：在 u 的子树中选 k 个点使它们两两 LCA 是 u 的方案数，对 v 也求同样的东西，

再把两者相乘就是最后的答案了

有可能u,v 存在祖孙关系，

不妨设 u 是 v 的祖先，那么 u 的子树就要改为以 v 的 方向作为根方向前提下的子树

然后就乱搞就行了

code：

#include<bits/stdc++.h>
#define del(a,i) memset(a,i,sizeof(a))
#define ll long long
#define inl inline
#define il inl void
#define it inl int
#define ill inl ll
#define re register
#define ri re int
#define rl re ll
#define mid ((l+r)>>1)
#define lowbit(x) (x&(-x))
#define INF 0x3f3f3f3f
using namespace std;
template<class T>il read(T &x){
	int f=1;char k=getchar();x=0;
	for(;k>'9'||k<'0';k=getchar()) if(k=='-') f=-1;
	for(;k>='0'&&k<='9';k=getchar()) x=(x<<3)+(x<<1)+k-'0';
	x*=f;
}
template<class T>il _print(T x){
	if(x/10) _print(x/10);
	putchar(x%10+'0');
}
template<class T>il print(T x){
	if(x<0) putchar('-'),x=-x;
	_print(x);
}
ll mul(ll a,ll b,ll mod){long double c=1.;return (a*b-(ll)(c*a*b/mod)*mod)%mod;}
it qpow(int x,int m,int mod){
	int res=1,bas=x%mod;
	while(m){
		if(m&1) res=(1ll*res*bas)%mod;
		bas=(1ll*bas*bas)%mod,m>>=1;
	}
	return res%mod;
}
const int MAXN = 1e5+5,mod = 998244353;
int n,m,L,u,v,k,head[MAXN],num_edge,dp[MAXN][505];
struct Edge{
	int next,to;
	Edge(){}
	Edge(int next,int to):next(next),to(to){}
}edge[MAXN<<1];
il add_edge(int u,int v){
	edge[++num_edge]=Edge(head[u],v),head[u]=num_edge;
	edge[++num_edge]=Edge(head[v],u),head[v]=num_edge;
}
it add(int x,int y){return x+y>=mod?x+y-mod:x+y;}
it mul(int x,int y){return 1ll*x*y%mod;}
int f[MAXN][18],dep[MAXN],sz[MAXN],deg[MAXN];
il DFS(int u,int fa){
	sz[u]=1,f[u][0]=fa,dep[u]=dep[fa]+1;
	for(ri i=1;i<=17;++i) f[u][i]=f[f[u][i-1]][i-1];
	for(ri i=head[u];i;i=edge[i].next){
		if(edge[i].to==fa) continue;
		DFS(edge[i].to,u);
		sz[u]+=sz[edge[i].to];
	}
}
it LCA(int u,int v){
	if(dep[u]<dep[v]) swap(u,v);
	for(ri i=17;i>=0;--i) if(dep[f[u][i]]>=dep[v]) u=f[u][i];
	if(u==v) return u;
	for(ri i=17;i>=0;--i)
		if(f[u][i]!=f[v][i])
			u=f[u][i],v=f[v][i];
	return f[u][0];
}
it jump(int u,int lca){//找到u到lca这条路径上除了lca外深度最小的点
	for(ri i=17;i>=0;--i)
		if(dep[f[u][i]]>dep[lca])
			u=f[u][i];
	return u;
}
il calc(int u){//dp[u][i]表示在u的子树中选择其中i颗上的点的方案数。
	dp[u][0]=1;
	for(ri i=head[u];i;i=edge[i].next){
		if(edge[i].to==f[u][0]) continue;
		for(ri j=deg[u];j;--j)
			dp[u][j]=add(dp[u][j],mul(dp[u][j-1],sz[edge[i].to]));
	}
	for(ri i=deg[u];i;--i)
		dp[u][i]=add(dp[u][i],mul(dp[u][i-1],n-sz[u]));
}
int fac[MAXN],ifac[MAXN],inv[MAXN];
il init(){
	for(ri i=1;i<=n;++i) calc(i);
	fac[0]=ifac[0]=inv[1]=1;
	for(ri i=1;i<=L;++i) fac[i]=mul(fac[i-1],i);
	ifac[L]=qpow(fac[L],mod-2,mod);
	for(ri i=L-1;i;--i) ifac[i]=mul(ifac[i+1],i+1);
	for(ri i=2;i<=n;++i) inv[i]=mul(mod-mod/i,inv[mod%i]);
}
it C(int n,int m){return mul(fac[n],mul(ifac[n-m],ifac[m]));}
int ans[MAXN],tmp[MAXN];
it solve(int u,int k,int t){
	for(ri i=1;i<=deg[u];++i) ans[i]=0;//ans表示在背包中去掉大小为t的部分后的答案
	for(ri i=1;i<=deg[u];++i) tmp[i]=dp[u][i]; //tmp表示原来的答案
	//由于背包问题具有交换性（加入背包顺序可以改变），所以我们可以看做t是最后被加入背包的
	//因为我们有tmp[i]=ans[i]+ans[i-1]*sz，且在加入最后一个之前dp[deg[u]]=0，所以我们可以倒着推出ans[i]
	//即ans[i-1]=(tmp[i]-ans[i])/sz
	for(ri i=deg[u];i;--i){
		ans[i-1]=mul(tmp[i],inv[t]);
		tmp[i]=0,tmp[i-1]=add(tmp[i-1],mod-ans[i-1]);
	}
	ri res=0;
	for(ri i=0;i<=min(deg[u],k);++i) res=add(res,mul(mul(fac[i],ans[i]),C(k,i)));
	return res;
}
int main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	read(n),read(m),read(L);
	for(ri i=1;i<n;++i) read(u),read(v),add_edge(u,v),++deg[u],++deg[v];
	DFS(1,0);
	init();
	for(ri i=1;i<=m;++i){
		read(u),read(v),read(k);
		if(dep[u]<dep[v]) swap(u,v);
		ri lca=LCA(u,v);
		if(lca!=v) print(mul(solve(u,k,n-sz[u]),solve(v,k,n-sz[v]))),puts("");
		else{
			ri t=jump(u,lca);
			print(mul(solve(u,k,n-sz[u]),solve(v,k,sz[t]))),puts("");
		}
	}
	return 0;
}