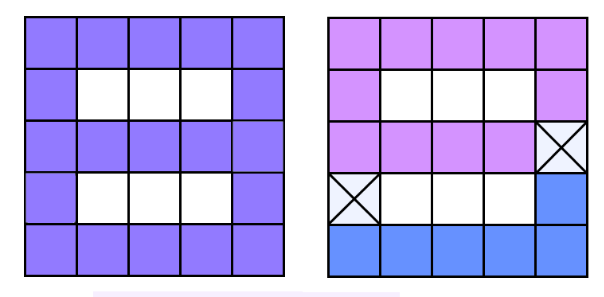
看起来非常神,但仅仅有三种情况 -1 , 1 ,2.....
You've gotten an n × m sheet of squared paper. Some of its squares are painted. Let's mark the set of all painted squares as A. Set A is connected. Your task is to find the minimum number of squares that we can delete from set A to make it not connected.
A set of painted squares is called connected, if for every two squares a and b from this set there is a sequence of squares from the set, beginning in a and ending in b, such that in this sequence any square, except for the last one, shares a common side with the square that follows next in the sequence. An empty set and a set consisting of exactly one square are connected by definition.
The first input line contains two space-separated integers n and m (1 ≤ n, m ≤ 50) — the sizes of the sheet of paper.
Each of the next n lines contains m characters — the description of the sheet of paper: the j-th character of the i-th line equals either "#", if the corresponding square is painted (belongs to set A), or equals "." if the corresponding square is not painted (does not belong to set A). It is guaranteed that the set of all painted squares A is connected and isn't empty.
On the first line print the minimum number of squares that need to be deleted to make set A not connected. If it is impossible, print -1.
5 4 #### #..# #..# #..# ####
2
5 5 ##### #...# ##### #...# #####
2
In the first sample you can delete any two squares that do not share a side. After that the set of painted squares is not connected anymore.
The note to the second sample is shown on the figure below. To the left there is a picture of the initial set of squares. To the right there is a set with deleted squares. The deleted squares are marked with crosses.
/**
* Created by ckboss on 14-10-8.
*/
import java.util.*;
public class CuttingFigure {
static int n,m;
static int[] dir_x = {0,0,1,-1};
static int[] dir_y = {1,-1,0,0};
static boolean[][] vis = new boolean[55][55];
static char[][] map = new char[55][55];
static boolean inmap(int x,int y){
return (x>=0&&x<n)&&(y>=0&&y<m);
}
static void dfs(int x,int y){
vis[x][y]=true;
for(int i=0;i<4;i++){
int X=dir_x[i]+x;
int Y=dir_y[i]+y;
if(inmap(X,Y)&&vis[X][Y]==false&&map[X][Y]=='#'){
dfs(X,Y);
}
}
}
static int CountNum(int x,int y){
for(int i=0;i<55;i++) Arrays.fill(vis[i],false);
if(inmap(x,y)) vis[x][y]=true;
int cnt=0;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(vis[i][j]==false&&map[i][j]=='#'){
dfs(i,j);
cnt++;
}
}
}
return cnt;
}
public static void main(String[] args){
Scanner in = new Scanner(System.in);
n=in.nextInt(); m=in.nextInt();
int nb=0;
in.nextLine();
for(int i=0;i<n;i++){
String line = in.nextLine();
for(int j=0;j<m;j++){
map[i][j]=line.charAt(j);
if(map[i][j]=='#') nb++;
}
}
if(nb<3){
System.out.println("-1");
return ;
}
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(CountNum(i,j)==1){
continue;
}
else {
System.out.println("1");
return ;
}
}
}
System.out.println("2");
}
}