1.词法分析
编译器的扫描或词法分析( lexical analysis)阶段可将源程序读作字符文件并将其分为若干个记号。
1.扫描处理
扫描程序的任务是从源代码中读取字符并形成由编译器的以后部分(通常是分析程序)处理的逻辑单元。
记号通常定义为枚举类型的逻辑项。例如,记号在C中可被定义为:
typedef enum
{ IF, THEN, ELS,EPLUS, MINUS, NUM, ID, ...}
TokenType;
扫描程序是一种格式匹配,所以需要研究扫描过程中的格式说明和识别方法,其中最主要的是正则表达式和有穷自动机。
2.正则表达式
正则表达式表示字符串的格式。正则表达式r完全由它所匹配的串集来定义。这个集合称为由正则表达式生成的语言( language generated by the regular expression),写作L(r)。此处的语言只表示“串的集合”,它与程序设计语言并无特殊关系(至少在此处是这样的)。
正则表达式r还包括字母表中的字符,但这些字符具有不同的含义:在正则表达式中,所有的符号指的都是模式。
2.1 正则表达式的定义
参考:https://www.runoob.com/regexp/regexp-syntax.html
现在通过讲解每个模式所生成的不同语言来描述正则表达式的含义。
1) 基本正则表达式 它们是字母表中的单个字符且自身匹配。空串用( epsilon )来表示,元符号ε(黑体)是通过设定L( ε) = {ε }来定义的,表示不包含任何字符的串。偶尔还需要写出一个与任何串都不匹配的符号,它的语言为空集(empty set),写作{ }。我们用符号Φ来表示,并写作L( Φ) = {}。请注意{ }和{ε}的区别:{ }集不包括任何串,而{ε}则包含一个没有任何字符的串。
2) 正则表达式运算 在正则表达式中有3种基本运算:① 从各选择对象中选择,用元字符|(竖线)表示。②连结,由并置表示(不用元字符)。③重复或“闭包”,由元字符*表示。
3) 从各选择对象中选择 如果r 和s 是正则表达式,那么正则表达式r | s 可匹配被r 或s 匹配的任意串。从语言方面来看,r | s 语言是r 语言和s 语言的联合(union),或L (r | s) = L (r)∪ (s)。
4) 连结 正则表达式r 和正则表达式s 的连结可写作rs,它匹配两串连结的任何一个串,其中第1个匹配r,第2个匹配s。
5) 重复 正则表达式的重复有时称为Kleene闭包((Kleene) closure),写作r *,其中r 是一个正则表达式。正则表达式r * 匹配串的任意有穷连结,每个连结均匹配r。
6) 运算的优先和括号的使用 在这3个运算中, *优先权最高,连结其次,| 最末。因此,a | b c * 就可解释为a | ( b ( c* )),而a b | c * d 却解释为( a b )| (( c* ) d )。
2.2 正则表达式的扩展
(1) 一个或多个重复
假若有一个正则表达式r,r 的重复是通过使用标准的闭包运算来描述,并写作r *。它允许r 被重复0次或更多次。0次并非是最典型的情况,一次或多次才是,这就要求至少有一个串匹配r,但空串却不行。例如在自然数中需要有一个数字序列,且至少要出现一个数字。如要匹配二进制数,就写作( 0 | 1 ) *,它同样也可匹配不是一个数的空串。当然也可写作
( 0 | 1 ) ( 0 | 1 ) *
但是这种情况只出现在用+代替*的这个相关的标准表示法被开发之前: r +表明r 的一个或多个重复。因此,前面的二进制数的正则表达式可写作:
( 0 | 1 ) +
(2) 任意字符
为字母表中的任意字符进行匹配需要一个通常状况:无需特别运算,它只要求字母表中的每个字符都列在一个解中。句号“ .”表示任意字符匹配的典型元字符,它不要求真正将字母表写出来。利用这个元字符就可为所有包含了至少一个b 的串写出一个正则表达式,如下所示:
. * b . *
(3) 字符范围
我们经常需要写出字符的范围,例如所有的小写字母或所有的数字。直到现在都是在用表示法a | b | . . . | z 来表示小写字母,用0 | 1 | . . . | 9来表示数字。还可针对这种情况使用一个特殊表示法,但常见的表示法是利用方括号和一个连字符,如[ a - z ]是指所有小写字母,[ 0 -9 ]则指数字。这种表示法还可用作表示单个的解,因此a | b | c可写成[ a b c ],它还可用于多个范围,如[ a - z A - Z ]代表所有的大小写字母。这种普遍表示法称为字符类( character class)。例如,[ A - Z ]是假设位于A和Z之间的字符B、C等(一个可能的假设)且必须只能是A和Z之间的大写字母(ASCII字符集也可)。但[ A - z ]则与[ A - Z a - z ]中的字符不匹配,甚至与ASCII字符集中的字符也不匹配。
(4) 不在给定集合中的任意字符
正如前面所见的,能够使要匹配的字符集中不包括单个字符很有用,这点可由用元字符表示“非”或解集合的互补运算来做到。例如,在逻辑中表示“非”的标准字符是波形符“ ~”,那么表示字母表中非a 字符的正则表达式就是~ a。非a、b 及c 表示为:
~ ( a | b | c )
在Lex中使用的表示法是在连结中使用插入符“^”和上面所提的字符类来表示互补。
例如,任何非a 的字符可写作[ ^ a ],任何非a、b 及c 的字符则写作:
[ ^ a b c ]
(5) 可选的子表达式
有关串的最后一个常见的情况是在特定的串中包括既可能出现又可能不出现的可选部分。例如,数字前既可有一个诸如+或-的先行符也可以没有。这可用解来表示,同在正则定义中是一样的:
natural = [0-9]+
signedNatural = natural | + natural | - natural
但这会很快变得麻烦起来,现在引入问号元字符r?来表示由r 匹配的串是可选的(或显示r 的0个或1个拷贝)。因此上面那个先行符号的例子可写成:
natural = [0-9]+
signedNatural= (+|-)? natural
3.有限自动机
3.1 NFA:不确定的有限自动机
1.定义


3.2 DFA:确定的有限自动机
1.定义

2.解释:
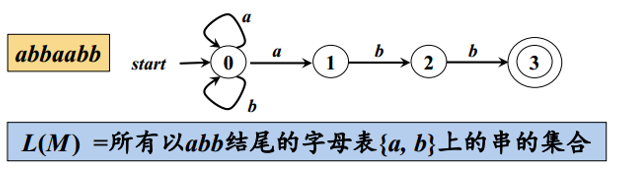
- 初始状态: 只有一个,由start箭头指向
- 终止状态: 可以有多个,用双圈表示
- L(M): 由一个有穷自动机M接收的所有串构成的集合,称为是该FA定义(或接收)的语言
- 最长前缀匹配原则
3.3 用代码实现有穷自定机
1.方法一
{starting in state 1}
if the next character is a letter then
advance the input;
{ now in state 2 }
while the next character is a letter or a digit do
advance the input; { stay in state 2 }
end while;
{ go to state 3 without advancing the input }
accept ;
else
{ error or other cases }
end if;
这个代码使用代码中的位置(嵌套于测试中)来隐含状态,这与由注释所指出的一样。如果没有太多的状态(要求有许多嵌套层)且DFA中的循环较小,那么就合适了。
2.方法二

利用状态变量和嵌套的case测试实现标识符DFA。
3.方法三
将DFA表示为数据结构并写成实现来自该数据结构的行为的“类”代码。转换表( transition table),或二维数组就
是符合这个目标的简单数据结构,它由表示转换函数T值的状态和输入字符来索引:

若给定了恰当的数据结构和表项,就可以在一个将会实现任何DFA的格式中编写代码了。下面的代码图解假设了转换被保存在一个转换数组T中,而T由状态和输入字符索引;先行输入的转换(即:那些在表格中未被括号标出的)是由布尔数组Advance给出,它们也由状态和输入字符索引;而由布尔数组A c c e p t给出的接受状态则由状态索引。下面就是代码图解:
state := 1; ch : = next input character; while not Accept[state] and not error(state) do newstate := T [s t a t e , c h]; if Advance [state,ch] then ch := next input char; state := newstate; end while; if Accept [state] then accept;
此算法称作表驱动( table driven),这是因为它们利用表格来引导算法的过程。表驱动方法有若干优点:代码的长度缩短了,相同的代码可以解决许多不同的问题,代码也较易改变(维护)了。但也有一些缺点:表格会变得非常大,使得程序要求使用的空间也变得非常大。
3.4 从正则表达式到DFA

将正则表达式翻译成DFA的最简单算法是通过中间构造,在它之中,正则表达式派生出一个NFA,接着就用该NFA构造一个同等的DFA。
3.4.1 从正则表达式到NFA
1) 基本正则表达式基本正则表达式格式a、ε或Φ,其中a表示字母表中单个字符的匹配,ε表示空串的匹配,Φ而则表示根本不是串的匹配。
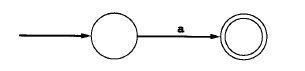
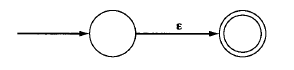
与正则表达式a等同的NFA 与ε等同的NFA
2) 并置我们希望构造一个与正则表达式rs等同的NFA,其中r 和s 都是正则表达式。
r的NFA:

注:圆角矩形的左边圆圈表示初始状态,右边的双圆表示接受状态,中间的3个点表示NFA中未显示出的状态和转换。
rs的NFA:

我们已将r 机的接受状态与s 机的接受状态通过一个- 转换连接在一起。新机器将r 机的初始状态作为它的初始状态,并将s 机的接受状态作为它的接受状态。很明显,该机可接受L (r s) =L (r) L (s) 的关系,它也对应于正则表达式rs。
3) 在各选项中选择我们希望在与前面相同的假设下构造一个与r | s 相对应的NFA。

该机接受语言L (r | s) = L (r)υL (s)。
4) 重复我们需要构造与r *相对应的机器,现假设已有一台与r 相对应的机器。那么就如下进行:
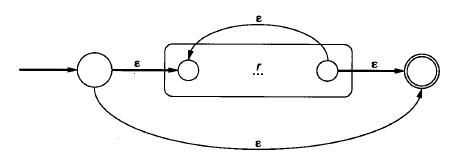
这里又添加了两个新的状态:一个初始状态和一个接受状态。该机中的重复由从r 机的接受状态到它的初始状态的新的-转换提供。
3.4.2 从NFA到DFA
消除ε- 转换涉及到了ε- 闭包的构造。子集构造----消除在单个输入字符上的多重转换涉及跟踪可由匹配单个字符而达到的状态的集合。
1) 状态集合的ε- 闭包
我们将单个状态s 的ε- 闭包定义为可由一系列的零个或多个ε- 转换能达到的状态集合。
2) 子集构造
对给定的NFA--M来构造DFA--$overline{M}$。首先计算M的初始状态的ε-闭包,构成$overline{M}$的初始状态。对于这个集合以及随后的每个集合,计算a字符之上的转化如下:
假设有状态的S集合字母表中的字符a,计算集合Sa={t|对
于S中的一些s,在a上有从s到t的转换}。接着计算$overline{S_{a}}$,它是Sa的闭包。
这就定义了子集构造中一个新状态和一个新转换$S-dfrac{a}{}
ightarrow overline{S_{a}}$。
继续这个过程直至不产生新的状态或转换。
例:

初始状态是$overline{1}=left{1,2,4 ight}$,存在字符a上的由状态2向状态3转换,而在a上没有来自状态1或状态4的转换,因此a上就有从{1,2,4}到 $overline{left{1,2,4 ight}}_{a}$ $=overline{left{ 3 ight}}$ $=left{2,3,4 ight}$的转换。由于再也没有来自一个字符上的1、2或4状态的转换了,因此就可将注意力转向新状态{ 2 , 3 , 4 }。此时在a 上有从状态2到状态3的转换,且也没有来自3或4状态的a- 转换,因此就有从{ 2 , 3 , 4 } 到
$ overline{left{1,2,4 ight}}_{a}=overline{left{3 ight}}=left{2,3,4 ight} $ 的转换,因而也就有从{ 2 , 3 , 4 }到它本身的a- 转换。