编译器实现（三）

1. 上下文无关文法及分析

上下文无关文法的规则是递归的。

识别这些结构的算法使用递归调用或显示管理的分析栈。经常使用的基本结构是一类树（分析树或语法树）。

算法大致可分为两种：自顶向下和由底向上

1.1 分析过程

分析函数将扫描程序生成的记号序列作为输入，并生成语法树作为输出：

1. 编译器中更多是多遍，后面的遍将语法树作为他们的输入。
2. 语法树的结构很大程度依赖语言特定的语法结构。
3. 错位处理，恢复继续分析。

1.2 上下文无关文法

同正则表达式类似，文法规则是定义在一个字母表或符号集之上。

1.2.1 上下文无关文法规则

文法规则：

exp → exp op exp | (exp) | number
op → + | - | *　

　　第1个规则定义了一个表达式结构（用名字e x p）由带有一个算符和另一个表达式的表达式，或一个位于括号之中的表达式，或一个数组成。第2个规则定义一个算符（利用名字o p）由符号+、-或*构成。

还有其他各种变形形式：

1.

2.

3.

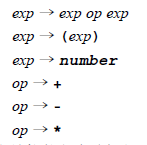
4.

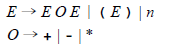
1.2.2 推导及由文法定义的语言

文法规则通过推导确定记号符号的正规串。推导 是在文法规则的右边进行选择的一个结构名字替换序列。推导以一个结构名字开始并以记号符号串结束。在推导的每一个步骤中，使用来自文法规则的选择每一次生成一个替换。

例：由文法规则进行推导

由推导从exp符号中得到的所有记号符号的串集是被表达式的文法定义的语言。

推导的结果集合记为：

　　

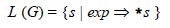
其中G代表表达式文法，s 代表记号符号的任意数组串（有时称为句子 ），而符号⇒*表示由如前所述的替换序列组成的推导（星号用作指示步骤的序列，这与在正则表达式中指示重复很相像）。由于它们通过推导“产生” L (G）中的串，文法规则因此有时也称作产生式 。

终结符，通俗的说就是不能单独出现在推导式左边的符号，也就是说终结符不能再进行推导。
不是终结符的都是非终结符。非终结符可理解为一个可拆分元素，而终结符是不可拆分的最
小元素。如：有α → β ，则α 必然是个非终结符。一般书上把非终结符用大写字母表示，而
终结符用小写字母表示。识别符号就是开始符。由文法产生语言句子的基本思想是：从识别符
号开始，把当前产生的符号串中的非终结符号替换为相应规则右部的符号串，直到最终全由终
结符号组成。这种替换过程称为推导或产生句子的过程，每一步成为直接推导或直接产生。 
例如： 
有文法G2[S]为： 
S->Ap 
S->Bq 
A->a 
A->cA 
B->b 
B->dB 
则表示：S 为开始符，S，A，B 为非终结符，而p,q,a,b,c,d 为终结符

1.3 分析树与抽象语法树

1.3.1 分析树

与推导相对应的分析树是一个作了标记的树，其内部的结点由非终结符标出，树叶节点由终结符标出，每个子节点都表示推导的一个步骤中的相关非终结符的替换。

例：

　　

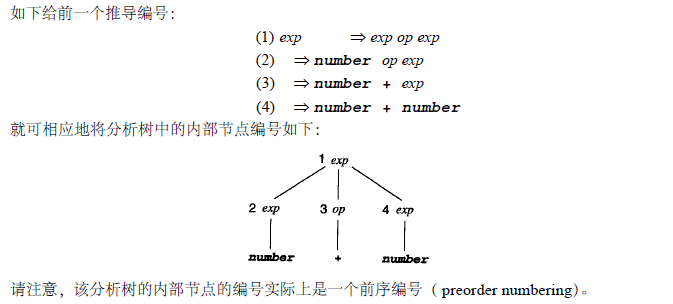
一般而言，分析树可与许多推导相对应。
最左推导
    是指它的每一步中最左的非终结符都要被替换的推导。与其相关的分析树的内部节点的前序编号相对应。
最右推导
    则是指它的每一步中最右的非终结符都要被替换的推导。最右推导则和后序编号相对应。

1.3.2 抽象语法树

分析树包含了比纯粹生成可执行代码所需更多的信息。抽象语法树去除了得到记号序列的分析过程，但包含了转换所需的所有信息，是真正的源代码记号序列的抽象表示。

　　　　　　　　

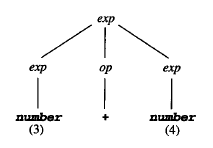
　　　　　分析树　　　　　　　　　

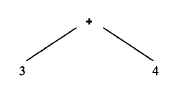
　　　抽象语法树

 1.4 二义性

分析树和语法树唯一地表达着语法结构，它们与表达最左和最右推导一样，但并不是对于所有推导都可以。不幸的是，文法有可能允许一个串有多于一个的分析树。例如在前面作为标准示例的简单整型算术文法中

　　exp → exp op exp | ( exp ) | n u m b e r
　　op → + | - | *
和串3 4 - 3 * 4 2，这个串有两个不同的分析树：

　　

有两个解决二义性的基本方法。

其一是：设置一个规则，该规则可在每个二义性情况下指出哪一个分析树（或语法树）是正确的。这样的规则称作消除二义性规则（disambiguating rule）。这样的规则的用处在于：它无需修改文法（可能会很复杂）就可消除二义性；它的缺点在于语言的语法结构再也不能由文法单独提供了。

另一种方法是将文法改变成一个强制正确分析树的构造的格式，这样就可以解决二义性了。当然在这两种办法中，都必须确定在二义性情况下哪一个树是正确的。这就再一次涉及到语法制导翻译原则了。我们所需的分析（或语法）树应能够正确地反映将来应用到构造的意义，以便将其翻译成目标代码。

优先权和结合性

为了处理文法中的运算优先权问题，就必须把具有相同优先权的算符归纳在一组中，并为每一种优先权规定不同的规则。

　　

else悬挂问题

　　例：文法：由于可选的else的影响，这个文法有二义性。

　　　　　　

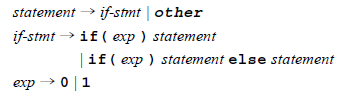
　　对：if (0) if (1) other else other  有两个分析树：

　　　　

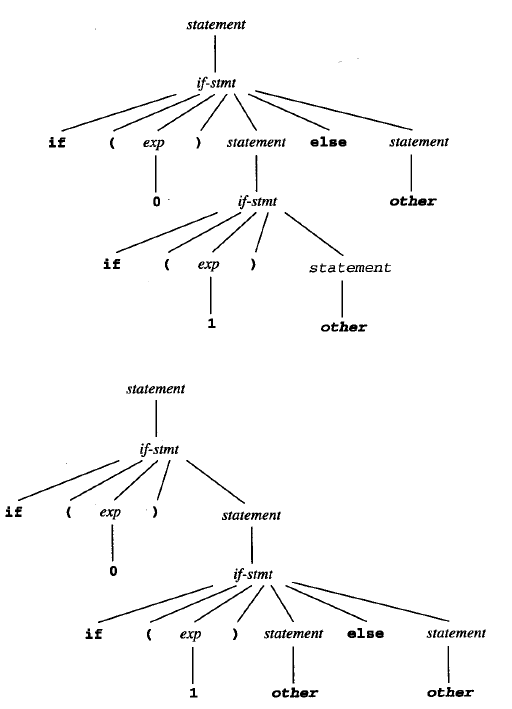
　　解决：

　　　　

　

1.5 扩展的表示法：EBNF和语法图

EBNF：参考：https://blog.csdn.net/cfy_qiangkeming/article/details/83288555

扩展的BNF，包含了重复和可选的结构。

重复：

　　重复是由文法规则中的递归表达，可能使用了左递归或右递归，一般规则：

　　　　

　　其中：α和β是终结符和非终结符的任意串，且在第1个规则中β不以A开始，在第2个规则中β不以A结束。

语法图

　　用作可视地表示E B N F规则的图形表示法称作语法图（ syntax diagram）。它们是由表示终结符和非终结符的方框、表示序列和选择的带箭头的线，以及每一个表示文法规则定义该非终结符的图表的非终结符标记组成。圆形框和椭圆形框用来指出图中的终结符，而方形框和矩形框则用来指出非终结符。

　　

1.6 上下文无关语言的形式特征

1.6.1 形式定义

定义　　上下文无关文法由以下各项组成：
1) 终结符（terminal）集合T。
2) 非终结符（nonterminal）集合N（与T不相交）。3) 产生式（production）或文法规则（grammar rule）A→a的集合P，其中A是N的一个
元素，a是（T ∪ N）*中的一个元素（是终结符和非终结符的一个可为空的序列）。
4) 来自集合N的开始符号（start symbol）。

文法G上的分析树（ parse tree）是一个带有以下属性的作了标记的树：

1) 每个节点都用终结符、非终结符或 标出。

2) 根节点用开始符号S标出。

3) 每个叶节点都用终结符或ε标出。

4) 每个非叶节点都用非终结符标出。

5) 如带有标记A∈N的节点有n 个带有标记X₁, X₂, . . . X_n 的孩子（可以是终结符也可以是非终结符），就有A→X1 , X2 , . . . Xn ∈P（文法的一个产生式）。

若上下文无关文法G有L=L(G)，就将串L的集合称作上下文无关语言。若存在串w∈ L (G)，其中w 有两个不同的分析树（或最左推导或最右推导），那么文法G就有二义性。