按是否涉及数据的内外存交换, 内部排序(记录个数不是很多的小文件) 外部排序(记录个数太多,不能一次将全部记录放入内存)
按策略划分 内部排序:
5、分配排序(桶排序,基数排序);
这里三个平均时间复杂度为n^2的排序(直接插入排序,冒泡,直接选择都是稳定的)。
常用的排序算法的时间复杂度和空间复杂度
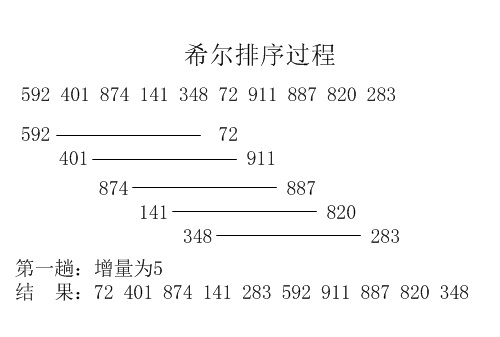
1:希尔排序http://blog.csdn.net/cjf_iceking/article/details/7951481
平均时间复杂度:希尔排序的时间复杂度和其增量序列有关系,这涉及到数学上尚未解决的难题;不过在某些序列中复杂度可以为O(n1.3);
空间复杂度:O(1)
稳定性:不稳定

5:分配排序:http://yaochaosheng.iteye.com/blog/995021
http://blog.csdn.net/kesalin/article/details/6260286
桶排序是在分配排序的基础上为相同元素或在同一个范围内的元素分配同一个桶,因此每个桶可以看做一个变长的链表
基数排序是将元素分等级从最次级到最高级不断进行递进的排序过程。
分配排序的基本思想:排序过程无须比较关键字,而是通过用额外的空间来"分配"和"收集"来实现排序,它们的时间复杂度可达到线性阶:O(n)。简言之就是:用空间换时间,所以性能与基于比较的排序才有数量级的提高!
排序算法基本操作:
比较关键字大小;改变指向记录的指针或者 移动记录本身。
待排序文件常用存储方式:
1)顺序表,对记录本身进行物理重排
2)链表,无需移动记录,修改指针。链式排序。
3)用顺序方式存储待排序的记录,但同时建立一个辅助表(包含关键字和指向记录位置的指针 组成的索引表)。
只对辅助表 进行物理重排。使用与难于在链表上实现,又需避免移动记录的排序方法。