JS实现最小生成树之克鲁斯卡尔（Kruskal）算法

 

克鲁斯卡尔算法打印最小生成树：

　　构造出所有边的集合 edges，从小到大，依次选出筛选边打印，遇到闭环（形成回路）时跳过。

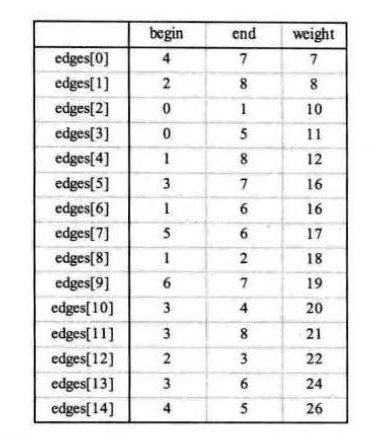
JS代码：

//定义邻接矩阵
let Arr2 = [
    [0, 10, 65535, 65535, 65535, 11, 65535, 65535, 65535],
    [10, 0, 18, 65535, 65535, 65535, 16, 65535, 12],
    [65535, 18, 0, 22, 65535, 65535, 65535, 65535, 8],
    [65535, 65535, 22, 0, 20, 65535, 65535, 16, 21],
    [65535, 65535, 65535, 20, 0, 26, 65535, 7, 65535],
    [11, 65535, 65535, 65535, 26, 0, 17, 65535, 65535],
    [65535, 16, 65535, 65535, 65535, 17, 0, 19, 65535],
    [65535, 65535, 65535, 16, 7, 65535, 19, 0, 65535],
    [65535, 12, 8, 21, 65535, 65535, 65535, 65535, 0],
]

let numVertexes = 9, //定义顶点数
    numEdges = 15; //定义边数

// 定义图结构  
function MGraph() {
    this.vexs = []; //顶点表
    this.arc = []; // 邻接矩阵，可看作边表
    this.numVertexes = null; //图中当前的顶点数
    this.numEdges = null; //图中当前的边数
}
let G = new MGraph(); //创建图使用

//创建图
function createMGraph() {
    G.numVertexes = numVertexes; //设置顶点数
    G.numEdges = numEdges; //设置边数

    //录入顶点信息
    for (let i = 0; i < G.numVertexes; i++) {
        G.vexs[i] = 'V' + i; //scanf('%s'); //ascii码转字符 //String.fromCharCode(i + 65);
    }
    console.log(G.vexs) //打印顶点

    //邻接矩阵初始化
    for (let i = 0; i < G.numVertexes; i++) {
        G.arc[i] = [];
        for (j = 0; j < G.numVertexes; j++) {
            G.arc[i][j] = Arr2[i][j]; //INFINITY; 
        }
    }
    console.log(G.arc); //打印邻接矩阵
}

function Edge() {
    this.begin = 0;
    this.end = 0;
    this.weight = 0;
}

function Kruskal() {
    let n, m;
    let parent = []; //定义一数组用来判断边与边是否形成环路
    let edges = []; //定义边集数组

    for (let i = 0; i < G.numVertexes; i++) {
        for (let j = i; j < G.numVertexes; j++) { //因为是无向图所以相同的边录入一次即可，若是有向图改为0
            if (G.arc[i][j] != 0 && G.arc[i][j] != 65535) {
                let edge = new Edge();
                edge.begin = i;
                edge.end = j;
                edge.weight = G.arc[i][j];
                edges.push(edge);
            }
        }
    }

    edges.sort((v1, v2) => {
        return v1.weight - v2.weight
    });

    console.log('**********打印所有边*********');
    console.log(edges);

    for (let i = 0; i < G.numVertexes; i++) {
        parent[i] = 0;
    }

    for (let i = 0; i < edges.length; i++) {
        n = Find(parent, edges[i].begin)
        m = Find(parent, edges[i].end)
        if (n != m) { //假如n与m不等，说明此边没有与现有生成树形成环路
            parent[n] = m;
            console.log("(%s,%s) %d", G.vexs[edges[i].begin], G.vexs[edges[i].end], edges[i].weight);
        }
    }
}


function Find(parent, f) { //查找连线顶点的尾部下标
    while (parent[f] > 0) {
        f = parent[f]
    }
    return f;
}

createMGraph();
console.log('*********打印最小生成树**********')
Kruskal();

打印结果：

代码部分过程解析:

 

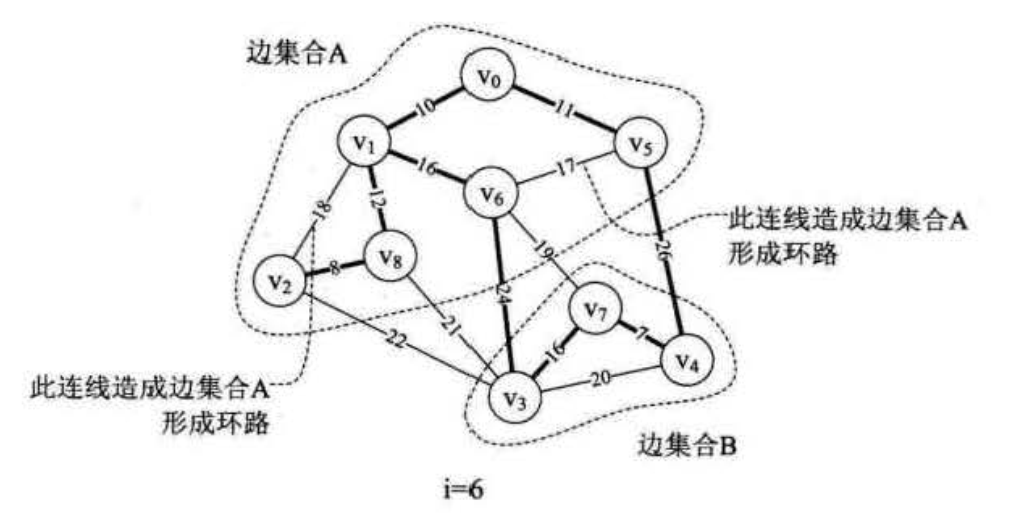
当i=7时，第82行，调用Find函数，会传入参数edges[7].begin=5。此时第94行，parent[5]=8>0,所以f=8，再循环得parent[8]=6。因parent[6]=0 所以Find返回后第82行得到n=6。而此时第83行，传入参数edges[7].end=6得到m=6。此时n=m，不再打印，继续下一循环。这就告诉我们，因为（V5,V6）使得边集合A形成了环路。因此不能将它纳入到最小生成树中。

当i=8时，与上面相同，由于边（V1,V2）使得边集合A形成了环路，因此不将它纳入最小生成树。

克鲁斯卡尔算法主要针对边展开，时间复杂度为 O(elog e)，e为图的边数，普利姆算法的时间复杂度为O(n²)，n为最小生成树的边数。所以，边数少（稀疏图）用克鲁斯卡尔算法，边数多（稠密图）用普利姆算法。

参考文献： 程杰《大话数据结构》