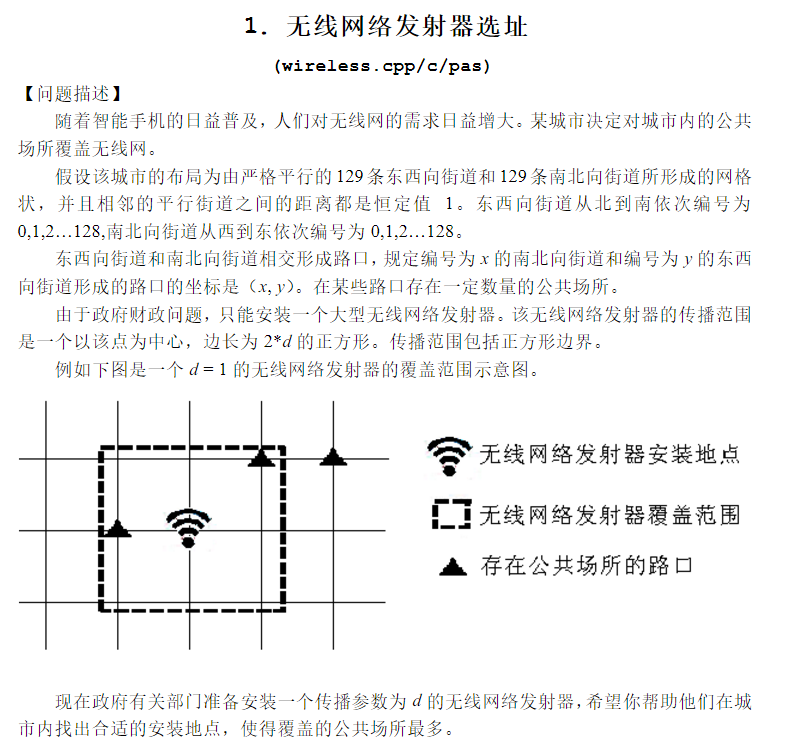
t1是一道大水题,数据范围0-128可以直接暴力枚举,还可以用二维前缀和优化一下,不过两种方法都可以过。
不过千万要注意不能数组越界!!!而且枚举的时候不能耍聪明直接从d开始,要从0开始。
话不多说,上代码
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; int a[200][200],ans; inline int read() { char ch=getchar(); int x=0; while(ch<'0'||ch>'9')ch=getchar(); while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+ch-'0'; ch=getchar(); } return x; } int main() { long long maxx=0; int d=read();int n=read(); for(register int i=1;i<=n;++i) { int x=read(),y=read(),k=read(); a[x][y]=k; } for(register int i=0;i<=128;++i) { for(register int j=0;j<=128;++j) { int cnt=0; int l=max(i-d,0),r=min(i+d,128),s=min(j+d,128),x=max(j-d,0); for(int k=l;k<=r;++k) for(int g=x;g<=s;++g) cnt+=a[k][g]; if(cnt>maxx)maxx=cnt,ans=1; else if(cnt==maxx)ans++; } } printf("%d %lld",ans,maxx); return 0; }

t2是一道奇奇怪怪的题,乍一看没有啥思路,但是细细一想就发现既然要求点可以通往重点,那么可以直接从终点开始跑一遍广搜(注意这个是跑反边),然后把能跑到的点打上标记。最后跑一边SPFA,但是要注意每次找到的点都要判断一下以它为起点的边的终点有没有被打上标记,然后甩开膀子使劲干就行了。
以下是代码
#include<cstdio> #include<cstring> #include<algorithm> #include<queue> #define maxm 200010 #define maxn 10010 using namespace std; int n,m,ecnt,vis[maxn<<2],viss[maxn<<2],head[maxn<<2],headd[maxn<<2],ecntt,dis[maxn<<2]; queue<int>q; struct edge { int u,v,next; }E[maxm],EE[maxm]; void addedge(int u,int v) { E[++ecnt].u=u; E[ecnt].v=v; E[ecnt].next=head[u]; head[u]=ecnt; EE[++ecntt].u=v; EE[ecntt].v=u; EE[ecntt].next=headd[v]; headd[v]=ecntt; } inline int read() { char ch=getchar(); int x=0; while(ch<'0'||ch>'9')ch=getchar(); while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+ch-'0'; ch=getchar(); } return x; } void bfss(int x) { q.push(x); vis[x]=1; viss[x]=1; while(!q.empty()) { int u=q.front(); q.pop(); for(int i=headd[u];i;i=EE[i].next) { int v=EE[i].v; vis[v]=1; if(!viss[v]) { q.push(v); viss[v]=1; } } } } void bfs(int x) { for(int i=1;i<=n;++i)dis[i]=1<<30; q.push(x); viss[x]=1; dis[x]=0; while(!q.empty()) { int u=q.front(); q.pop(); for(int i=head[u];i;i=E[i].next) { int flg=0; int v=E[i].v; if(!vis[v])continue; for(int j=head[v];j;j=E[j].next) { int vv=E[j].v; if(!vis[vv])flg=1; } if(flg)continue; dis[v]=min(dis[v],dis[u]+1); if(!viss[v]) { q.push(v); viss[v]=1; } } } } int main() { freopen("road.in","r",stdin); freopen("road.out","w",stdout); n=read(),m=read(); for(int i=1;i<=m;++i) { int u=read(),v=read(); addedge(u,v); } int s=read(),t=read(); bfss(t); if(!vis[s]) { printf("-1 "); return 0; } memset(viss,0,sizeof(viss)); bfs(s); if(dis[t]==(1<<30)) { printf("-1 "); return 0; } printf("%d ",dis[t]); return 0; }

t3乍一看发现好像可以直接暴力枚举然后加一个check就行了,但是接下来一看数据范围

惊了!!!
这是什么玩意儿。
不过根据同余定理,既然那一长串的东西等于0,那么它mod一个数p也等于0,但是这玩意儿不能反推。那我们可以枚举很多个质数p,并且让这些质数的乘积大于m的1e6就行了,因为如果存在一个数mod所有选的质数都等于0,那么这个数应该是这些质数的公倍数,但是解的范围最大到1e6,所以这个办法可行。
下面是代码
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; typedef long long LL; typedef double db; inline int read() { int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-')f=-1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+ch-'0'; ch=getchar(); } return x*f; } const int MAXN=110; int n,m,pri[]={6529,7451,8363,9281,9829},a[5][MAXN],pre[5][MAXN],val[5][10010],ans1,ans2[1000010]; void readBignum(int j) { int f=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-')f=-1; ch=getchar(); } while(ch>='0'&&ch<='9') { for(int i=0;i<5;++i) a[i][j]=(a[i][j]*10+ch-'0')%pri[i]; ch=getchar(); } for(int i=0;i<5;++i) a[i][j]*=f; return; } int cal(int x) { int ret=0; for(int i=0;i<=n;++i)ret=(ret+a[x][i]*pre[x][i]%pri[x])%pri[x]; if(ret<0)ret+=pri[x]; return ret; } bool check(int x) { for(int i=0;i<5;++i) if(val[i][x%pri[i]])return false; return true; } int main() { //freopen("equation.in","r",stdin); //freopen("equation.out","w",stdout); n=read();m=read(); for(int i=0;i<=n;++i)readBignum(i); for(int i=0;i<5;++i) { for(int j=1;j<pri[i];++j) { pre[i][0]=1; for(int k=1;k<=n;++k)pre[i][k]=(pre[i][k-1]*j)%pri[i]; val[i][j]=cal(i); } } for(int i=1;i<=m;++i)if(check(i))ans2[++ans1]=i; printf("%d ",ans1); for(int i=1;i<=ans1;++i)printf("%d ",ans2[i]); return 0; }