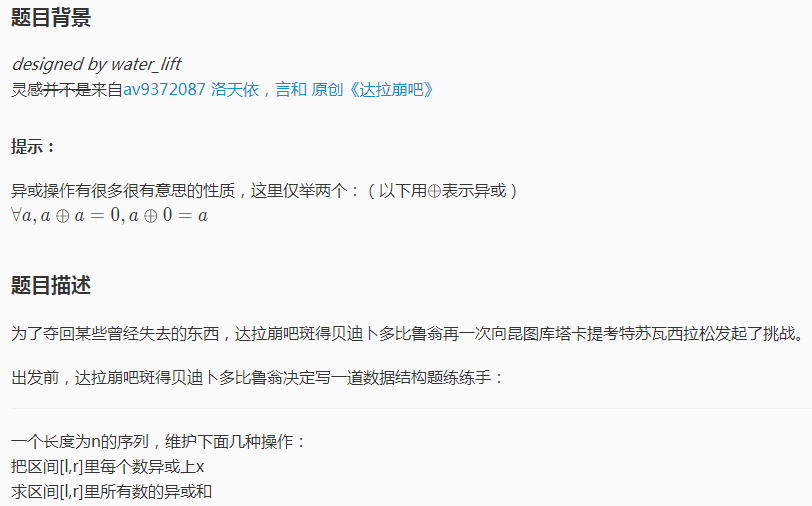
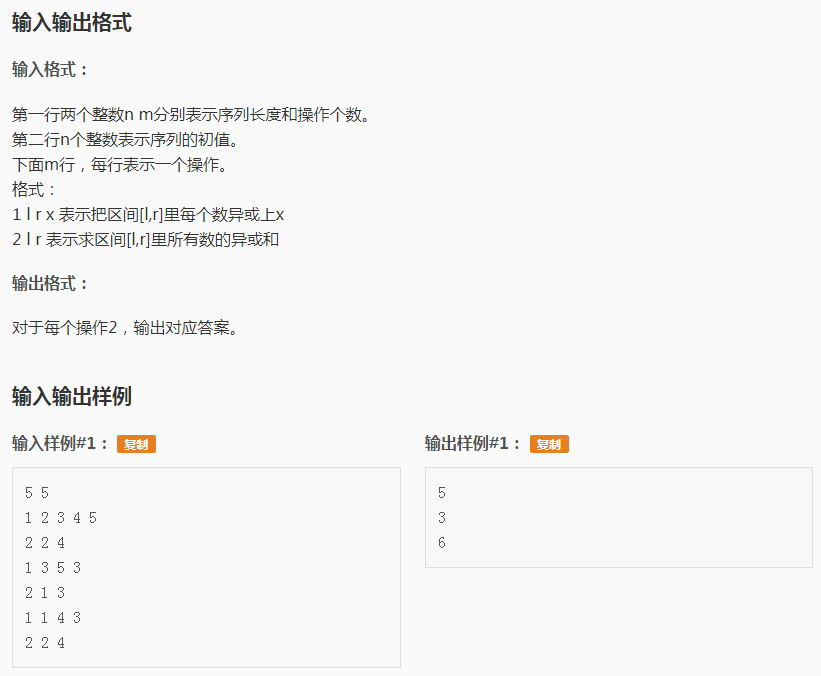
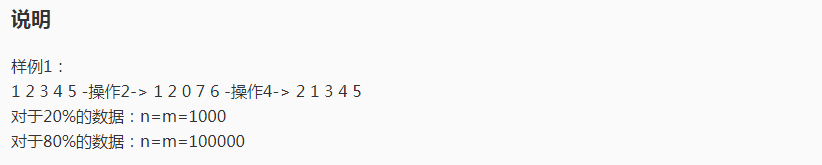
考试的一道附加题~
一看题目描述:把区间[l,r]里每个数异或上x,求区间[l,r]里所有数的异或和,这明显的要用数据结构或RMQ吧。
恩,所以正解就是线段树啦,至于树状数组行与否,不知道~
water_lift:这不是sb题嘛?线段树板子题都不会?把加法操作改成异或操作不就好啦?
其实好像真的是这样的,将加法操作改成了乘法操作;
然后你会发现自己只得了20分的暴力分,没错!相当于没写线段树!
因为线段树区间修改需要用到一个非常重要的东西:
懒标记

为什么要用到这个,直接暴力递归不好吗?
问得好!
假设我们每进行一次加法或减法操作我们就要从根节点一直递归到它儿子再递归回来,这样做好像没什么问题,但是,太耗时!
我们不如将这个区间内的所有元素做上一个懒标记!(顾名思义,懒标记很懒嘛,查到它它才改,不查就不改!真是壮士!)
这个懒标记是干嘛滴呢?假设我们对一个区间进行了n次操作,每次操作都给这个区间加上Ai(i从1~n),不做懒标记的话我们就要递归n次,树一大节点一多直接T得飞起!
所以我们就给这个区间的元素做上懒标记,每次懒标记加上要加上的Ai的值,但是不往下递归,所以到n次操作后这个区间的元素的懒标记就是:A1+A2+A3……+An,这样我们一次递归加上懒标记就好啦。
举个例子:

sum是这个区间内的总和相对于初始化增加了多少,inc是这个区间的每个元素相对于初始化增加了多少。
然后我们可以进行第一步操作:让[2,7]的每个元素增加2
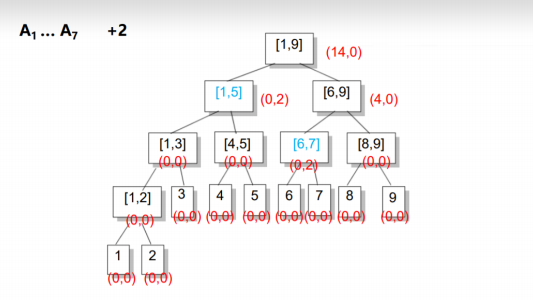
在全部的大区间[1,9]内,由于1~7都在这个区间内,所以总和相对于一开始的是增加了2*7=14,所以sum的值为14;但是[1,9]又不完全被包含在[1,7]内,所以我们不能更新inc值(看inc的定义,8和9不能+2)
因为区间[1,9]内还有元素不用+2,所以我们要继续往下找:
我们找到了区间[1,5]和区间[6,9],我们发现:区间[1,5]全部都在[1,7]内,所以区间[1,5]的inc值就可以更新为2了,sum值就是5*2=10;但是区间[6,9]还有元素不在区间[1,7]的范围内所以我们将这个区间继续往下找,同时将这个区间的sum值更新为4;
[6,9]可以分成[6,7]和[8,9],我们发现:区间[6,7]全部都在[1,7]以内,所以将区间[6,7]的inc值更新为2,sum值为2*2=4。到这步我们就发现[1,7]以内已经全部被找过了,所以我们就找完了!
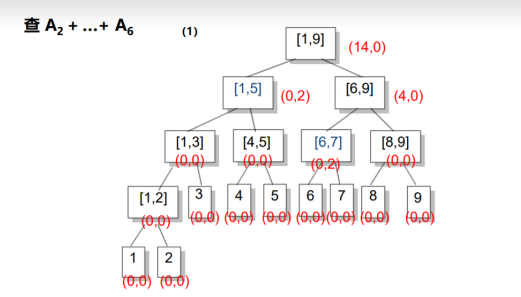
接下来我们查询[1,6]的和:
还是按照原来的思路:从根节点开始找,发现[1,9]并不完全被包含在所查区间内,所以我们就去找它的儿子;
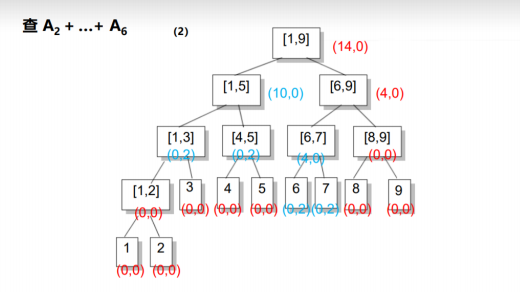
我们找到了[1,5],发现并不完全被包含在[2,6]内,所以我们继续往下找,并将inc值传给它的两个儿子;找到了[1,3]和[4,5],我们发现区间[4,5]全部被包含在内了,所以我们直接返回sum值+原区间和就好啦,sum=inc*len(区间长度)=2*2=4,但是[1,3]并不完全被包含在内,所以我们将[1,3]的inc值传给它的儿子,并继续往下找:
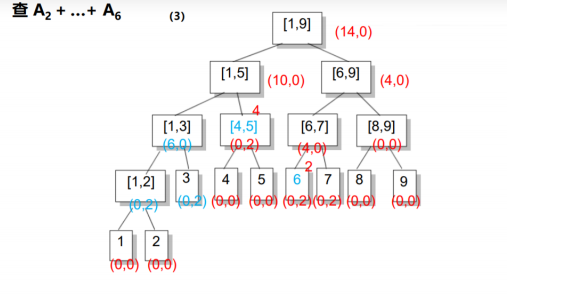
我们找到了[1,2]和区间[3,3](就是3),我们发现3完全被包含在所查区间内了,所以我们直接返回sum值+原区间和就好啦,sum=inc*len(区间长度)=2*1=2;但是区间[1,2]并不完全被包含在内,所以继续从它的儿子里面找,并将inc值传给儿子:
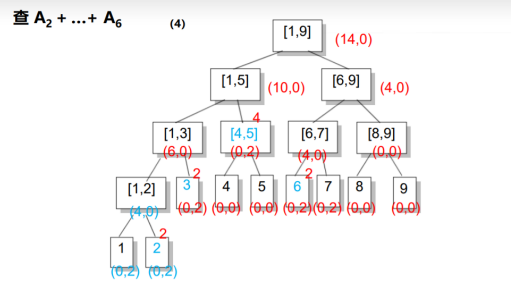
我们找到了1和2,1不在所查区间内就不管它了(不清楚懒标记inc值),我们发现2在所查区间内,所以直接返回sum值+原区间和就好啦,sum的公式就不用说了...
到这里的话,大家应该都会懒标记了QwQ~,毕竟前面讲的辣么详细。
但是还是会TLE几个点,我们继续找原因!
我们看到题目中给出的提示,它有什么用呢?


#include<iostream> #include<cstdio> using namespace std; int n,m,cz,x,y,k; int sum[400001],a[200001],lazy[400001]; //注意开4倍空间比较保险 void init(int node,int x,int y) //预处理一下 { if(x==y) sum[node]=a[x]; //叶子结点,直接赋值 else { int mid=(x+y)>>1; init(node*2,x,mid); //找左儿子 init(node*2+1,mid+1,y); //找右儿子 sum[node]=sum[node*2]^sum[node*2+1]; //更新父亲结点 } lazy[node]=0; } void pushdown(int node,int l,int r) //标记下传过程 { int mid=(l+r)>>1; lazy[node*2]^=lazy[node]; //下传给左儿子 lazy[node*2+1]^=lazy[node]; //下传给右儿子 sum[node*2]^=lazy[node]*((mid-l+1)%2); //更新左儿子的sum,用到了上面讲的优化2:更新奇数次就是更新一次,更新偶数次就是没更新 sum[node*2+1]^=lazy[node]*((r-mid)%2); lazy[node]=0; //注意清空,这里不是标记永久化 } void add(int node,int l,int r,int x,int y,int k) //区间[x,y]的每个数都异或上k { if(l>=x&&r<=y) //当前分解的区间[l,r]被完全包含在[x,y]里的话,直接更新 { sum[node]^=k*((r-l+1)%2); //优化2 lazy[node]^=k; //更新懒标记 return ; } pushdown(node,l,r); //先要标记下传 int mid=(l+r)>>1; if(x<=mid) add(node*2,l,mid,x,y,k); //与左区间有交集就去找左区间 if(y>=mid+1) add(node*2+1,mid+1,r,x,y,k); //与右区间有交集就去找右区间 sum[node]=sum[node*2]^sum[node*2+1]; //再更新父亲结点的sum } int ask(int node,int l,int r,int x,int y) //询问区间[x,y]内的异或和 { if(l>=x&&r<=y) return sum[node]; //被[x,y]包含的话就直接返回 pushdown(node,l,r); int res=0,mid=(l+r)>>1; if(x<=mid) res^=ask(node*2,l,mid,x,y); //与左区间有交集就去找左区间 if(y>=mid+1) res^=ask(node*2+1,mid+1,r,x,y); //与右区间有交集就去找右区间 return res; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&a[i]); init(1,1,n); for(int i=1;i<=m;i++) { scanf("%d%d%d",&cz,&x,&y); if(cz==1) { scanf("%d",&k); //[x,y]异或上k add(1,1,n,x,y,k); } else printf("%d ",ask(1,1,n,x,y)); //询问[x,y]的异或和 } return 0; }