这一次是交流测试?边交流边测试(滑稽
挖地雷

这个题是一个递推问题。
首先我们看第一个格子,因为它只影响了它的上面和右上面这两个地方是否有雷。
我们可以分3种情况讨论:
1. 第一个格子的数字是2;
2. 第一个格子的数字是1;
3. 第一个格子的数字是0;
显然对于第1种情况和第3种情况,我们可以确定前两个空的埋雷情况:
第1种情况就是前两个空都埋雷了,第3种情况就是钱两个空都没有埋雷;
第二种情况我们需要再往下细分:第一个空埋雷,第二个空不埋雷;第一个空不埋雷,第二个空埋雷;
我们根据样例来分析递推情况:
首先根据第一个格子的数字是2,我们可以推断出前两个空肯定是有雷的:
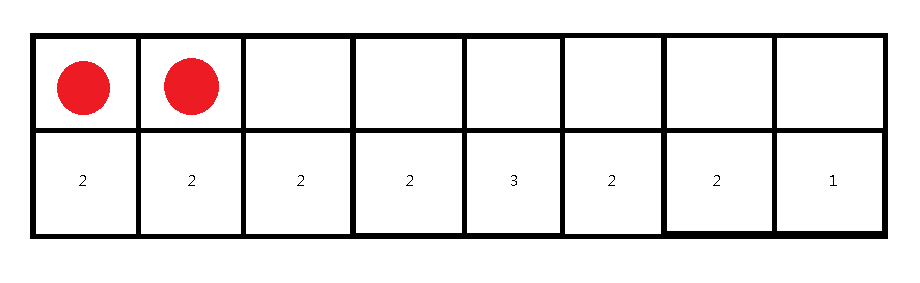
接下来我们考虑第二个格子上的数字对埋雷情况造成的影响,考虑到我们在考虑第 i 个格子上的数字时,第 1~i 个空已经确定下来了(是否埋雷),所以对于第2个格子及以后,它真正能确定的空也就是第 i + 1 个,根据样例可知,第三个空是不埋雷的:
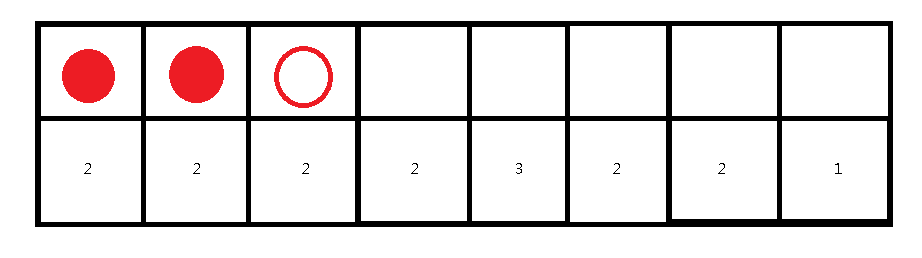
接下来考虑第三个格子上的数字对埋雷情况造成的影响,前三个空已经确定了,所以只能确定第四个空的情况,根据样例可知,第四个空是埋雷的:

以此类推,当我们考虑第 i 个格子上的数字对答案造成的影响的时候,实际上只能确定第 i + 1 个空的情况,对于具体的是否埋雷,我们还要看第 i - 1 ,i 个空的埋雷情况与第 i 个格子的数字的关系,轻松得到如下关系:
我们设 tot 是第 i - 1 ~ i 个空埋了多少个雷,vis [ i ] 表示第 i 个空是否埋雷,a [ i ] 表示第 i 个格子的数字是多少,则 tot 可以用下面一段代码求出:
for(int i=k-1;i<=k;i++) //当前考虑第k个格子上的数字对答案的影响 if(vis[i]) tot++;
有了这个 tot 有什么用呢?它决定着第 i + 1 个空是否埋雷,特别的,还能判断是否有解!
若 a [ k ] - tot = 1,说明第 i + 1个空需要埋雷;
若 a [ k ] - tot = 0,说明第 i + 1个空不需要埋雷;
若 a [ k ] - tot >=2,说明无解; //一个格子最多放一个雷,你却还有两个以上的雷需要放,肯定无解
若 a [ k ] - tot < 0;说明无解; //明明只需要放 a [ k ] 个,你光前两个空放的都比 a [ k ] 多了,肯定无解
说句题外话,第四个关系式我当时没想到,然后就 65 了QwQ~
代码也很好写,就是这样的(其实就是套上去的):
if(a[k]-tot==1) vis[k+1]=1; if(a[k]-tot==0) vis[k+1]=0; if(a[k]-tot>=2) return ; //一个格子最多放一个雷,你却还有两个以上的雷需要放,肯定无解 if(a[k]-tot<0) return ; //明明只需要放a[k]个,你光前两个空放的都比a[k]多了,肯定无解 search(k+1); //找下一个格子
还有一个小细节需要考虑到:
我们前面已经说了第 i 个格子的数字的实际影响是第 i + 1个空,所以说我们遍历第 n - 1个格子的时候不就把雷给埋完了?那第 n 个格子有啥子用?
这里我就用第 n 个格子的数字再来判断一下我们的埋雷情况是否合法,当我们遍历到第 n 个格子时,我们需要看一下 vis [ n - 1 ] + vis [ n ] 是否等于 a [ n ] 即可。
So ,我们就可以上完整代码啦:
#include<iostream> #include<cstdio> #include<cstring> using namespace std; int n,bj,tot; int a[10001],vis[10001]; void search(int k) { tot=0; //在k对应的三个格子中,已经埋了多少雷 for(int i=k-1;i<=k;i++) if(vis[i]) tot++; //求tot if(k==n) //当我们遍历第n个格子,进一步判断是否合法 { if(a[n]==tot) bj=1; //如果等于,说明合法 return ; } if(a[k]-tot==1) vis[k+1]=1; if(a[k]-tot==0) vis[k+1]=0; if(a[k]-tot>=2) return ; //一个格子最多放一个雷,你却还有两个以上的雷需要放,肯定无解 if(a[k]-tot<0) return ; //明明只需要放a[k]个,你光前两个空放的都比a[k]多了,肯定无解 search(k+1); //找下一个格子 } int main() { //freopen("bomp.in","r",stdin); //freopen("bomp.out","w",stdout); scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); if(a[i]<0||a[i]>3) //这里好坑的,一定要特判一下 { cout<<"No answer"<<endl; return 0; } } if(a[1]==2) //分情况讨论 { vis[1]=1; vis[2]=1; search(2); } if(a[1]==0) search(2); if(a[1]==1) //细分埋一个雷的情况 { vis[1]=1; //先使第一个空埋雷 search(2); if(!bj) //没找到解再让第二个空埋雷 { memset(vis,0,sizeof(vis)); vis[2]=1; search(2); } } if(bj) { for(int i=1;i<=n;i++) cout<<vis[i]<<" "; } else cout<<"No answer"<<endl; return 0; }