T1 地雷

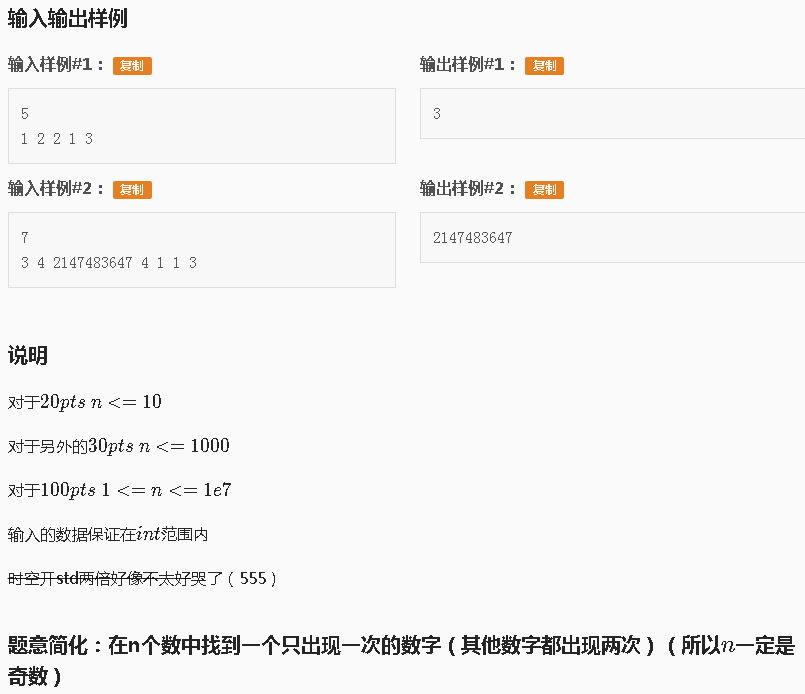
题目很简单呢,就是求哪个数只出现了一次就可以了哦~
我一开始的想法是桶排(这也是最单纯最简单的想法吧~),但是空间开 232 肯定会炸的,而且时间好像也会炸掉。
然后左边的 ych 大佬小声说了一句:“得换个算法。”
嗯,确实要换个算法,然后我就觉得新算法一定是不用开数组,直接输完数据就能出答案的那种!
然后不知道怎么就想到了 zhx 讲博弈论的时候输入的同时将 ……(一些稀奇古怪的东西) 异或起来就是答案,这不正好跟我理想的新算法很像嘛?
异或异或?咦,又想到了六月底那次考试有个叫【音乐会】达拉崩吧 · 上 的毒瘤题,上面给的两条提示:

对呀,两个相同的数异或起来就是 0!
所以我们可以将所有的数都异或起来,只要有两个相同的就变成 0 了,那么最后剩下的不就是那个落单的了嘛?
所以代码就出来了鸭~:
#include<iostream> #include<cstdio> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<1)+(a<<3)+(ch-'0'); ch=getchar(); } return a*x; } int n,x,ans; int main() { n=read(); for(int i=1;i<=n;i++) { x=read(); ans^=x; //求每个数的异或和 } printf("%d",ans); return 0; }
T2【BIO】RGB三角形




题目要求就是先给出一行 n 个有 ' R ' , ' G ' , ' B ' 这三个字符的字符串,然后相邻的两个如果相同,那么新产生的字符也相同;如果相邻两个字符不相同,那么新产生的字符是不同于这两个字符的另一个字符。求最后只剩下一个字符的时候那个字符是多少。
其实这是个结论题,看这个数据范围就是要用结论做的。
首先我们可以证明一个小结论:
当 n = 4 时,最后答案只由两段的字符决定:

证明 (特别鸣谢 qyf):

那么我们就可以得到这样一个大体框架:

然后这样:

一层一层往上推,然后就可以得到一个最后的规律:
如果 n = 3k + 1,则最后的答案就是由两段的字符决定!
有了这个结论,我就可以说我的思路啦:
我先打表求出 1e7 范围内所有的 3 的幂次方,然后找到最大的小于等于 n 的那个 3 的幂次方(设为 3k),然后从 n 个字符中找区间长度为 3k 的所有区间,利用上面的结论把它们变成一个字符,直到长度 <4 为止,剩下的自己暴力求出就好了:


#include<iostream> #include<cstdio> using namespace std; int n,len; long long three[16]={1,3,9,27,81,243,729,2187,6561,19683,59049,177147,531441,1594323,4782969,14348907}; char s[10000001]; char read() { char a=getchar(); if(a!='R'&&a!='G'&&a!='B') a=getchar(); return a; } char check(char a,char b) { if(a==b) return a; if(a=='R'&&b=='G'||a=='G'&&b=='R') return 'B'; if(a=='R'&&b=='B'||a=='B'&&b=='R') return 'G'; if(a=='G'&&b=='B'||a=='B'&&b=='G') return 'R'; } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) s[i]=read(); len=n; for(int i=15;i>=1;i--) { if(len>three[i]) //找到最大的小于len的3的次幂 { for(int j=three[i]+1;j<=len;j++) { s[j-three[i]]=check(s[j-three[i]],s[j]); } len-=three[i]; i++; //还有可能再拆一次 } } //处理长度小于等于3的情况 if(len==1) printf("%c",s[1]); else if(len==2) printf("%c",check(s[1],s[2])); else if(len==3) printf("%c",check(check(s[1],s[2]),check(s[2],s[3]))); return 0; }
T3【qbxt】复读警告



一道动态规划题目~
我们设 f [ i ][ j ] 表示当前是第 i 个数,前面选上的数的和模 key 后等于 j 的方案数;
考虑状态转移方程:
我们看这个状态设置有点像 01背包问题啊,那么状态转移方程就要像 01背包那样考虑:
我们可以考虑当前的数选不选!
1. 如果不选当前数,那么和就没有发生变化,则 f [ i ][ j ] = f [ i-1 ][ j ];
2. 如果选上了当前数,我们设加上当前数 a [ i ] 后的和再模 key 得到的余数是 j,假设未加上当前数 a [ i ] 时的和模 key 的余数是 k,那么显然 j = (k + a [ i ])% key;
那么我们就得到:k = ( j - a [ i ] % key )% key;所以我们要在考虑前 i-1 个数的时候,这个和模 key 必须是 k,加上 a [ i ] 后才能是 j,那么就有转移方程:
f [ i ][ j ] = f [ i-1 ][ k ]
我们发现这好像就是背包的状态转移方程qwq,那么 for 循环两层分别枚举两个维度就好啦:
#include<iostream> #include<cstdio> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<1)+(a<<3)+(ch-'0'); ch=getchar(); } return a*x; } const int mod=1e9+7; int n,key; long long a[1005],f[1005][1005]; //当前考虑到第i个数,和模key为j的方案数 int main() { n=read(); key=read(); for(int i=1;i<=n;i++) a[i]=read(); f[0][0]=1; for(int i=1;i<=n;i++) { for(int j=0;j<key;j++) { int k=((j-a[i])%key+key)%key; f[i][j]=f[i-1][j]+f[i-1][k]; f[i][j]%=mod; } } printf("%lld",f[n][0]%mod); //考虑到第n个数,模key为0(被key整除)的方案数 return 0; }