原题链接 https://www.luogu.org/problem/P3825



闲话时刻
本蒟蒻第 2 道通过的黑题 ,果然还是有人说水。。。
我觉得这个题出的很好,建边的时候细节很多,码量稍大,劝大家切的时候一定要细心了,不然就会像我一样把 “ = ” 打成 “;” 然后调了一天;
题目大意
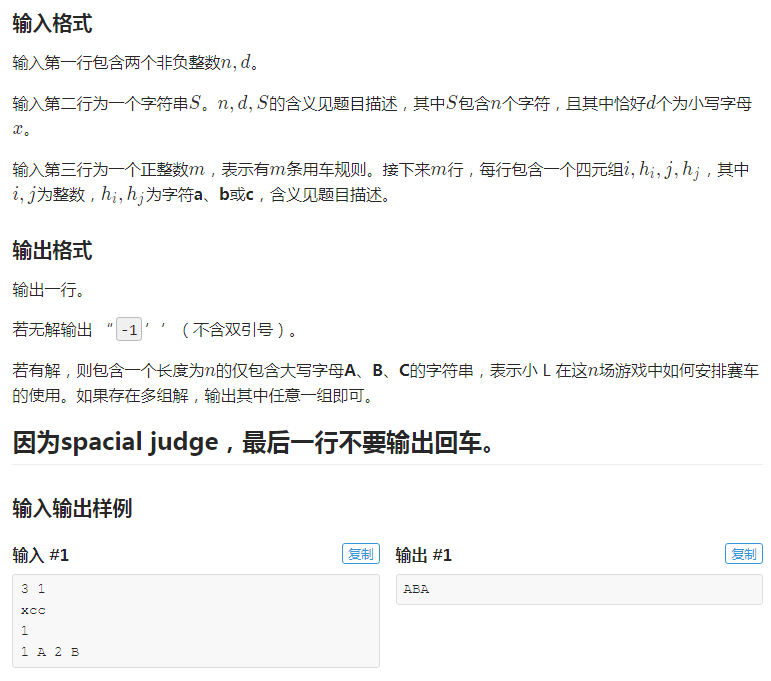
有 n 个点,每个点有三种取值,至多只有 d 个变量可以取到三种取值,其余的都只有一种不能取,还有 m 个关系限制式,问是否有解,有解输出方案数;
题解
还没有掌握好 2 - SAT 的童鞋戳这里;
①. 先考虑 d = 0 的情况:
此时每场游戏只能选择两种不同类型的赛车,发现是一个裸的 2-SAT 问题;
考虑怎么给点编号:
对于一场游戏 s,如果地图是类型 a,那么可选的赛车类型为 ' B ' 和 ' C ',那么 ' B ' 的编号就是 s,' C ' 的编号就是 s+n;如果地图是类型 b,那么可选的赛车类型为 ' A ' 和 ' C ',那么 ' A ' 的编号就是 s, ' C ' 的编号就是 s+n;如果地图的类型是 c,那么可选的赛车类型为 ' A ' 和 ' B ',那么 ' A ' 的编号就是 s,' C ' 的编号就是 s+n;
总的来说就是字母小的编号靠前,字母大的编号靠后;
int get(int k,char s) //在第k个地图上,类型为s的赛车的编号是多少 { //S[k]表示第k个地图的类型 if(S[k]=='a') //只能用赛车'B'和'C' { if(s=='B') return k; return k+n; } if(S[k]=='b') //只能用赛车'A'和'C' { if(s=='A') return k; else return k+n; } if(S[k]=='c') //只能用赛车'A'和'B' { if(s=='A') return k; return k+n; } }
搞定了编号的问题,现在考虑怎么建边:
设一场游戏能使用的两种赛车的类型分别是 i,i ' ;
对于每个特殊要求四元组(a,ha,b,hb),表示如果第 a 场游戏用了类型为 ha 的赛车,第 b 场游戏必须使用类型为 hb 的赛车,我们要分一下三种情况考虑:
<1> 如果第 a 场游戏由于地图的限制本来就不能使用类型为 ha 的赛车,那么我们不需要建任何边,直接 continue;
<2> 如果第 a 场游戏能使用类型为 ha 的赛车,但是第 b 场游戏由于地图的限制不能使用类型为 hb 的赛车,就说明第 a 场游戏是不能使用类型为 ha 的赛车的,不然就无解了,那么我们连边 < ha , ha ' > 表示第 a 场游戏只能用类型为 ha ' 的赛车;
<3> 如果第 a 场游戏能使用类型为 ha 的赛车,并且第 b 场游戏能使用类型为 hb 的赛车,那么我们根据限制连边 < ha , hb > 表示如果我们第 a 场游戏选择了类型为 ha 的赛车,那么第 b 场游戏必须选择类型为 hb 的赛车;反之,如果我们第 b 场游戏没有使用类型为 hb 的赛车,说明第 a 场游戏一定没有选择类型为 ha 的赛车,于是我们再连边 < hb ' , ha ' > ( 逆否命题与原命题等价 );
建完边后,我们对所有点进行一次 tarjan 求强联通分量,然后再判断是否有解,若有解就输出强联通分量较小的那辆赛车就好了(这个不需要多说了吧qwq)
int get(int k,char s) //在第k个地图上,类型为s的赛车的编号是多少 { //S[k]表示第k个地图的类型 if(S[k]=='a') //只能用赛车'B'和'C' { if(s=='B') return k; return k+n; } if(S[k]=='b') //只能用赛车'A'和'C' { if(s=='A') return k; else return k+n; } if(S[k]=='c') //只能用赛车'A'和'B' { if(s=='A') return k; return k+n; } } int fan(int a) //求在一场游戏中编号为a的赛车对应的另一辆赛车是多少 { if(a>n) return a-n; //如果这辆赛车的编号大,则另一辆赛车的编号小 return a+n; //如果这辆赛车的编号小,则另一辆赛车的编号大 } bool work() { clean(); for(int i=1;i<=m;i++) { a=num[i][1];ha=s[i][1]; //如果第a场游戏使用了类型为ha的赛车,则第b场游戏必须使用类型为hb的赛车 b=num[i][2];hb=s[i][2]; if(S[a]==ha+32) continue; //情况<1>:如果第a场游戏本来就不能使用类型为ha的赛车,直接continue int n1=get(a,ha); //求出在第a场游戏的地图上类型为ha的赛车的编号 int n2=get(b,hb); //求出在第b场游戏的地图上类型为hb的赛车的编号 if(S[b]==hb+32) //情况<2>:如果是第b场游戏不能使用类型为hb的赛车 add(n1,fan(n1)); //那么第a场游戏只能使用类型为ha'的赛车了 else //情况<3>:若第a场游戏能用类型为ha的赛车,且第b场游戏能用类型为hb的赛车 { add(n1,n2); //第a场游戏若用类型为ha的赛车,则第b场游戏必须用类型为hb的赛车 add(fan(n2),fan(n1)); //反之若第b场游戏没用类型为hb的赛车,则第a场游戏没有类型为ha的赛车 } } for(int i=1;i<=2*n;i++) //tarjan求强联通分量 { if(!dfn[i]) tarjan(i); } for(int i=1;i<=n;i++) //判无解情况 { if(scc[i]==scc[i+n]) return 0; } return 1; //否则有解 }
②. 然后考虑 d ≠ 0 的情况:
然后部分 3-SAT?表示没见过qwq
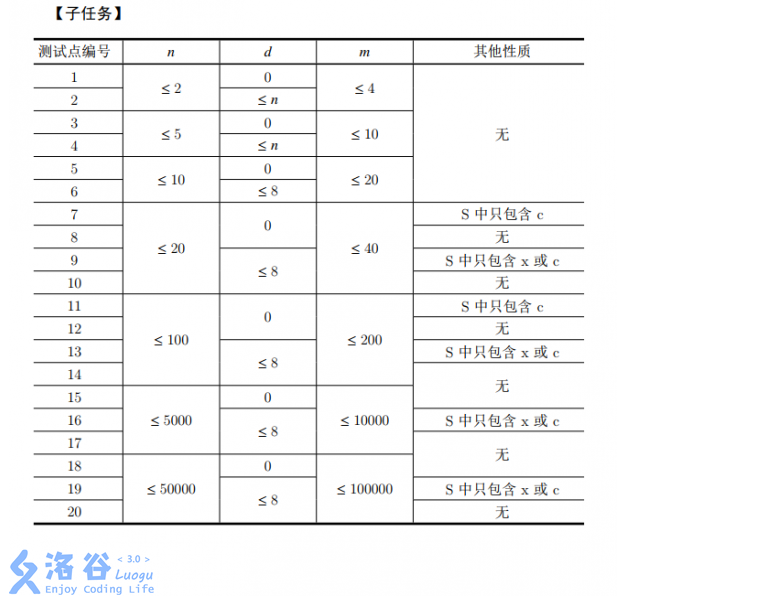
观察到 d 的范围很小,最大只有 8,所以推测最后的复杂度可能是一个 O ( Xd )的复杂度;
考虑可以去枚举每个 x 地图上使用什么哪两个类型的赛车,换而言之我们可以枚举每个 x 地图是 a,b,c 三类地图的哪一类,时间复杂度 O((n+m)* 3d),显然过不去;
考虑怎么优化:
其实我们只要枚举是 a,b,c 类地图中的两种就好了,假如以 a,b 地图为例吧:若是 a 地图就说明在此 x 地图上可以用类型为 ' B ' 和 ' C ' 的两种赛车,若是 b 地图就说明在此 x 地图上可以用类型为 ' A ' 和 ' C ' 的两种赛车,这样三种类型的赛车都在此 x 地图上试过了,不就涵盖了所有的情况了?
dfs 部分的代码:
void dfs(int k) //我们已经枚举到了第k个x型地图了 { if(k>d) //枚举完所有的x型跑道了 { if(work()) bj=1; //跑2-sat看看此时有没有解 return ; } for(int i=0;i<2;i++) //看看把它搞成哪种类型的地图(不能选哪种型号的赛车) { S[where[k]]=i+'a'; //这里将x型地图变成a,b这两种类型的地图 dfs(k+1); if(bj) return ; //有解直接返回 } }
奉上完整代码:
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<cstring> #include<vector> using namespace std; long long read() { char ch=getchar(); long long a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<1)+(a<<3)+(ch-'0'); ch=getchar(); } return a*x; } const int N=1e6; int n,m,d,a,b,bj,top,tim,edge_sum,scc_sum; int st[N],dfn[N],low[N],vis[N],scc[N],head[N],where[10],num[N][3]; char s[N][3],S[N],ha,hb; struct node { int from,next,to; }A[N]; void add(int from,int to) { edge_sum++; A[edge_sum].to=to; A[edge_sum].next=head[from]; A[edge_sum].from=from; head[from]=edge_sum; } void tarjan(int u) { dfn[u]=low[u]=++tim; st[++top]=u; vis[u]=1; for(int i=head[u];i;i=A[i].next) { int v=A[i].to; if(!dfn[v]) { tarjan(v); low[u]=min(low[u],low[v]); } else if(vis[v]) low[u]=min(low[u],dfn[v]); } if(dfn[u]==low[u]) { scc_sum++; while(st[top]!=u) { vis[st[top]]=0; scc[st[top]]=scc_sum; top--; } vis[st[top]]=0; scc[st[top]]=scc_sum; top--; } } void clean() { memset(dfn,0,sizeof(dfn)); memset(low,0,sizeof(low)); memset(scc,0,sizeof(scc)); memset(vis,0,sizeof(vis)); memset(st,0,sizeof(st)); memset(head,0,sizeof(head)); memset(A,0,sizeof(A)); edge_sum=0;scc_sum=0; tim=0;top=0; } int get(int k,char s) //在第k个地图上,类型为s的赛车的编号是多少 { //S[k]表示第k个地图的类型 if(S[k]=='a') //只能用赛车'B'和'C' { if(s=='B') return k; return k+n; } if(S[k]=='b') //只能用赛车'A'和'C' { if(s=='A') return k; else return k+n; } if(S[k]=='c') //只能用赛车'A'和'B' { if(s=='A') return k; return k+n; } } int fan(int a) //求在一场游戏中编号为a的赛车对应的另一辆赛车是多少 { if(a>n) return a-n; //如果这辆赛车的编号大,则另一辆赛车的编号小 return a+n; //如果这辆赛车的编号小,则另一辆赛车的编号大 } bool work() { clean(); for(int i=1;i<=m;i++) { a=num[i][1];ha=s[i][1]; //如果第a场游戏使用了类型为ha的赛车,则第b场游戏必须使用类型为hb的赛车 b=num[i][2];hb=s[i][2]; if(S[a]==ha+32) continue; //情况<1>:如果第a场游戏本来就不能使用类型为ha的赛车,直接continue int n1=get(a,ha); //求出在第a场游戏的地图上类型为ha的赛车的编号 int n2=get(b,hb); //求出在第b场游戏的地图上类型为hb的赛车的编号 if(S[b]==hb+32) //情况<2>:如果是第b场游戏不能使用类型为hb的赛车 add(n1,fan(n1)); //那么第a场游戏只能使用类型为ha'的赛车了 else //情况<3>:若第a场游戏能用类型为ha的赛车,且第b场游戏能用类型为hb的赛车 { add(n1,n2); //第a场游戏若用类型为ha的赛车,则第b场游戏必须用类型为hb的赛车 add(fan(n2),fan(n1)); //反之若第b场游戏没用类型为hb的赛车,则第a场游戏没有类型为ha的赛车 } } for(int i=1;i<=2*n;i++) //tarjan求强联通分量 { if(!dfn[i]) tarjan(i); } for(int i=1;i<=n;i++) //判无解情况 { if(scc[i]==scc[i+n]) return 0; } return 1; //否则有解 } void dfs(int k) //我们已经枚举到了第k个x型地图了 { if(k>d) //枚举完所有的x型跑道了 { if(work()) bj=1; //跑2-sat看看此时有没有解 return ; } for(int i=0;i<2;i++) //看看把它搞成哪种类型的地图(不能选哪种型号的赛车) { S[where[k]]=i+'a'; //这里将x型地图变成a,b这两种类型的地图 dfs(k+1); if(bj) return ; //有解直接返回 } } int main() { n=read();read(); for(int i=1;i<=n;i++) { S[i]=getchar(); if(S[i]=='x') where[++d]=i; //where[i]记录第i个x地图的位置 } m=read(); for(int i=1;i<=m;i++) //输入一定要处理好 scanf("%d %c %d %c",&num[i][1],&s[i][1],&num[i][2],&s[i][2]); dfs(1); //从第一个x型地图开始枚举 if(!bj) //无解的情况 { printf("-1"); return 0; } for(int i=1;i<=n;i++) //有解就输出方案数 { if(S[i]=='a') //如果是a型地图,就不能选择类型为A的赛车 { if(scc[i]<scc[i+n]) printf("B"); //选择强连通分量编号小的最为最后的选择 else printf("C"); } if(S[i]=='b') //如果是b型地图,就不能选择类型为B的赛车 { if(scc[i]<scc[i+n]) printf("A"); //选择强连通分量编号小的最为最后的选择 else printf("C"); } if(S[i]=='c') //如果是c型地图,就不能选择类型为C的赛车 { if(scc[i]<scc[i+n]) printf("A"); //选择强连通分量编号小的最为最后的选择 else printf("B"); } } return 0; }