割点 —— Tarjan 算法

由于对于这一块掌握的十分不好，所以在昨天做题的过程中一直困扰着我，好不容易搞懂了，写个小总结吧 qwq~

割点

概念

在无向连通图中，如果将其中一个点以及所有连接该点的边去掉，图就不再连通，那么这个点就叫做割点 。

比如我们现在有一个图：

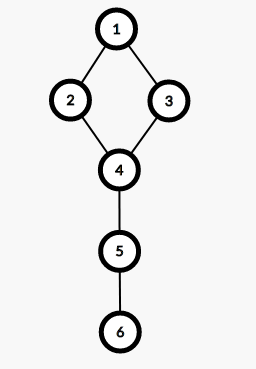
如果我们将 4 号节点及它的所有边全部删去，那么这个图就变得不再联通，所以 4 号点是一个割点：

同理，5 号节点也是一个割点：

怎么求割点 

我们可以用 Tarjan 算法去求割点；

有两个关键的数组：

dfn [ i ] ：表示编号为 i 的点在 dfs 过程中是第几个被遍历到的（时间戳）；

low [ i ]：表示编号为 i 的点的子树中的节点所能到达的最小时间戳是多少； 

这两个数组不需要再多多介绍了吧？想必大家在学 Tarjan 算法的时候都熟练掌握了；

重点说一下怎么求割点：

首先，割点都是定义在无向图中的，所以我们可以任选一个点为根（一般是 1 号节点）开始 Tarjan 算法；

考虑什么样的点才可能是割点呢？

我们上面提到了 4 号节点是一个割点，那是因为删除 4 号节点及其所连的边后，1 2 3 和 5 6 就不连通了，也就是说，除了 4 号结点所连的边外，5 6 号结点没有其余的边连向 1 2 3，也就是说没有返祖边；

既然如此，4 号点之下的点所能到达的最小时间戳一定不超过 dfn [ 4 ] ，不然就到了 4 号点之上了；

那么我们就得到了一个判断一个点是否是割点的条件：

如果一个点 u 满足 low [ u ] >= dfn [ u ]，那么点 u 就是一个割点；

但是……

根节点的 dfn 和 low 值初始值都为 1，之后再怎么更新 low [ root ] 始终都是 1，那这么一搞的话根结点始终是割点？

显然不是啊！

对于根结点，我们要另想办法qwq~

看一棵十分丑陋的树：

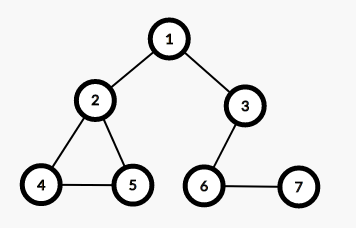
发现如果将 1 结点及其所有的边删掉，那么 2 5 4 和 3 6 7 将不连通，说明此时 1 是一个割点；

发现此时根节点有两棵互不相连的子树；

所以我们可以记录根节点有几棵互不相连的子树，如果大于 1 棵的话，根节点就是一个割点；  

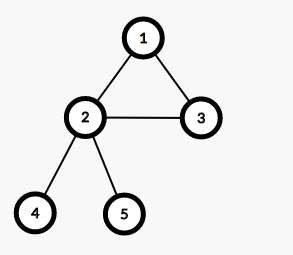
如果有几棵子树是相连的，那么会在 Tarjan 的时候将它们算成一棵子树：

P3388 【模板】割点（割顶）  的代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
int read()
{
    char ch=getchar();
    int a=0,x=1;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        a=(a<<1)+(a<<3)+(ch-'0');
        ch=getchar();
    }
    return a*x;
}
int n,m,tim,top,edge_sum,scc_sum,tot;
int head[1000001],dfn[1000001],low[1000001],vis[1000001],st[1000001],u[1000001],v[1000001],ans[1000001];
queue<int> q;
struct node
{
    int from,to,next;
}a[1000001];
void add(int from,int to)
{
    edge_sum++;
    a[edge_sum].next=head[from];
    a[edge_sum].from=from;
    a[edge_sum].to=to;
    head[from]=edge_sum;
}
void tarjan(int u,int root)
{
    int child=0;                                 //记录根节点有几棵互不相连的子树 
    dfn[u]=low[u]=++tim;                          
    for(int i=head[u];i;i=a[i].next)
    {
        int v=a[i].to;
        if(!dfn[v]) 
        {
            tarjan(v,root);
            low[u]=min(low[u],low[v]); 
            if(low[v]>=dfn[u])                   //如果 
            {
                child++;                         //记录根节点有多少个互不相连的子树 
                if(u!=root||child>1) ans[u]=1;   //如果不是根节点,那么直接就是割点了;如果是根节点,并且互不相连的子树个数超过1棵,则也是割点 
            }
        }
        else low[u]=min(low[u],dfn[v]);    
    }    
}
int main()
{
    n=read();m=read();
    for(int i=1;i<=m;i++)
    {
        u[i]=read();
        v[i]=read();
        add(u[i],v[i]);                          //建双向边     
        add(v[i],u[i]);
    }
    for(int i=1;i<=n;i++)                        //有可能图不是联通的,要多进行几次Tarjan 
    {
        if(!dfn[i]) tarjan(i,i);
    }    
    for(int i=1;i<=n;i++)                        //求割点个数 
    {
        if(ans[i]) tot++;
    }
    printf("%d
",tot);
    for(int i=1;i<=n;i++)
    {
        if(ans[i]) printf("%d ",i);              //输出每个割点 
    }
    return 0;
}

再看个例题：

题目大意 

给定一张无向图，求每个点被封锁之后有多少个有序点对 ( x , y ) ( x != y ,1 <= x , y <= n ) 满足 x 无法到达 y； 

题解

很显然这是一个让你求割点的问题，所以我们根据被封锁的这个点 u 是不是割点来分两种情况讨论：

1. 如果 u 不是割点：

即把 u 和它有关的所有边都去除后图依然联通，那么这个图只有 u  是独立在外面的，由于求的是有序点对，所以除了 u 以外的 n-1 个点作为一个大的连通图对 u 加边，即为 2 ∗ ( n − 1 ) 对；

2. 如果 u 是割点：

假如 u 是割点，那么会把图分为 a 个连通块以及 u 本身，由于 Tarjan 在求割点的过程中是一棵搜索树往下遍历，所以除了它和它的子树外，还会有其他剩余点共同构成另一个连通块；

删掉 u 后肯定有一些子树不与大联通块联通了（满足条件 low [ v ] >= dfn [ u ]），设这些子树的根节点分别为 1，2，3，……，a，这些子树所包含的结点数为 tot = size [ 1 ] + size [ 2 ] + size [ 3 ] + …… + size [ a ]；

那么点 u 的最后答案就是：

ans[u] = size[1] * (n-size[1]-1) + size[2] * (n-size[2]-1) + …… + size[a] * (n-size[a]-1) + tot * (n-tot-1) + 2*(n-1)；   

解释一下式子怎么来的：

首先在求割点的过程中，每次遇到 low [ v ] >= dfn [ u ]，就要把 u 的答案加上 size [ v ] * ( n - size [ v ] - 1 )，这些是子树不能到达外面结点（没有 u）的贡献；

考虑完子树对外的贡献后，同样外面的结点也不能到达这些子树内的结点；

子树内的所有点是 tot，那么外面的点就是 n - tot - 1，那么外面结点对子树内的贡献再加上就是 tot * ( n - tot - 1 ) ；

然后再考虑点 u 的单独的贡献，显然它无法到达任何点，同样任何点也无法到达它，那么答案再加上 2*(n-1)；

最后注意开 long long 哦~

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<vector>
using namespace std;
long long read()
{
    char ch=getchar();
    long long a=0,x=1;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        a=(a<<1)+(a<<3)+(ch-'0');
        ch=getchar();
    }
    return a*x;
}
const int N=1e6;
long long n,m,top,tim,num,root,edge_sum;
long long head[N],yes[N],dfn[N],low[N],st[N],vis[N],size[N],u[N],v[N],ans[N],son[N];
struct node
{
    int next,to,from;
}a[N];
void add(int from,int to)
{
    edge_sum++;
    a[edge_sum].from=from;
    a[edge_sum].to=to;
    a[edge_sum].next=head[from];
    head[from]=edge_sum;
}

void tarjan(int u)                                       //Tarjan求割点            
{
    dfn[u]=low[u]=++tim;
    size[u]=1;                                           //求以点u为根的树的大小 
    long long child=0,tot=0;
    for(int i=head[u];i;i=a[i].next)
    {
        int v=a[i].to;
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
            size[u]+=size[v];
            if(low[v]>=dfn[u])  
            {
                child++;                                 //子树棵数++  
                ans[u]+=size[v]*(n-size[v]-1);           //统计这些子树内的结点对外结点的贡献 
                tot+=size[v];                            //统计这些子树内的结点总数 
                if(u!=root||child>1) yes[u]=1;           //如果u不是根节点,那么直接就是割点了;如果是根节点,并且有超过1棵子树的话,也是割点 
            }
        }
        else low[u]=min(low[u],dfn[v]);
    }
    if(yes[u]) ans[u]+=tot*(n-tot-1)+2*(n-1);            //tot*(n-tot-1)是外结点对子树内结点的贡献,2*(n-1)是点u对所有点的贡献 
}
int main()
{
    n=read();m=read();
    for(int i=1;i<=m;i++)
    {
        u[i]=read();v[i]=read();
        add(u[i],v[i]);
        add(v[i],u[i]);
    }
    root=1;
    tarjan(1);                                           //题目的信息说明了这个图原本是联通的,所以我们求一次Tarjan就好了 
    for(int i=1;i<=n;i++) if(!yes[i]) ans[i]=2*(n-1);    //不是割点的话,答案就是2*(n-1) 
    for(int i=1;i<=n;i++) printf("%lld
",ans[i]);
    return 0;
}

希望CSP不要考到这一块的内容啊qwq

最后祝大家 CSP rp ++