P3396 哈希冲突

原题链接  https://www.luogu.com.cn/problem/P3396

题目大意

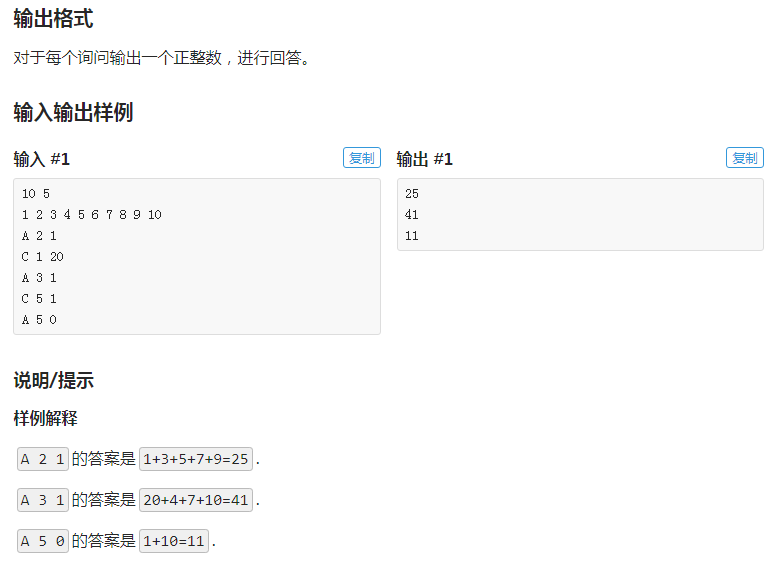
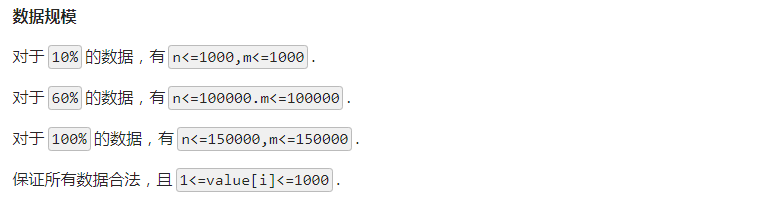
给你一个长度为 n 的序列和 m 个操作，每次操作有两种类型：

1. 询问下标模 x 后为 y 的所有数之和；

2. 修改第 x 个数；

题解

先想想暴力怎么搞：

对于第 1 种操作，我们可以 O（n）的枚举求和，对于第 2 种操作，我们可以 O（1）修改；

    long long ans=0;
    for(int i=y;i<=n;i+=x) ans+=a[i];  //暴力枚举加和 
    printf("%lld
",ans);

总的时间复杂度为 O（nm），n² 过 15w？显然不行；

考虑一下第一种操作为什么跑的慢。

如果模数 x 很小时，我们上面的那层 for 循环的复杂度更接近 O（n）；反之，如果模数 x 很大时，复杂度反而会小；

这就提供了我们一种思路：

只有当 x 比较大的时候我们才暴力，如果 x 很小，我们直接记录答案！

那么 x 什么时候才算大呢？

一般我们钦定 x > √n 的时候我们就暴力；

这种算法有个响当当的名字： 

根号算法

根号算法是一种很常见的算法；
常见的根号思想有：双向搜索，根号分类讨论，根号重建，复杂度平衡，以及一些根号级别的数据结构如分块和莫队；
这些算法一般是多种暴力算法的结合，一般具有较低的思维难度和编码难度；

——ImmortalCO猫

有的时候，我们可以对一个题想出两个暴力，各有各自的长处和短处。

如果我们能对数据范围进行分块处理，或者两个暴力分别算之后拼接在一起，就用两个合在一起的暴力，实现了正解。

通常这个分界点可以取到 n−−√n

所以叫根号算法。

通过根号算法，我们就能实现两种操作时间复杂度的均分了 。

我们用 dp [ i ][ j ] 记录模 i 为 j 的所有下标所对应的数的和；（这里数组只需开到 √n）

O（n√n）预处理出答案：

    for(int i=1;i<=n;i++)  //枚举每个数 
        for(int j=1;j<=sqrt(n);j++)  //枚举模几
            dp[j][i%j]+=a[i]; 

对于第 1 种操作，如果所给的模数 x < √n，那么我们直接输出答案；否则我们暴力枚举；

时间复杂度 O（√n）

        if(C=='A')   //求模x为y的和
        {
            if(x<=sqrt(n)) printf("%lld
",dp[x][y]);  //直接输出 
            else                
            {
                long long ans=0;
                for(int i=y;i<=n;i+=x) ans+=a[i];  //暴力枚举加和 
                printf("%lld
",ans);
            }
        } 

对于第 2 种操作，我们在将第 x 个数更新的同时，也要把 dp 数组更新一遍；

时间复杂度 O（√n）

        for(int i=1;i<=sqrt(n);i++)  //更新第x个数所涉及到的所有的池
            dp[i][x%i]+=y-a[x]; 
        a[x]=y;

总体时间复杂度 O（n√n），这样我们就用几乎暴力的算法过掉了本题qwq

Code：

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int read()
{
    char ch=getchar();
    int a=0,x=1;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        a=(a<<1)+(a<<3)+(ch-'0');
        ch=getchar();
    }
    return a*x;
}
const int N=150005;
int a[N];
long long dp[400][400];  //dp[i][j]:模i为j的所有下标所对应的数的和,只需开到√n 
int n,m,x,y;
char C;
int main()
{
    n=read();m=read();
    for(int i=1;i<=n;i++) a[i]=read();
    for(int i=1;i<=n;i++)  //枚举每个数 
        for(int j=1;j<=sqrt(n);j++)  //枚举模几
            dp[j][i%j]+=a[i]; 
    while(m--)
    {
        cin>>C;
        x=read();y=read();
        if(C=='A')   //求模x为y的和
        {
            if(x<=sqrt(n)) printf("%lld
",dp[x][y]);  //直接输出 
            else     //若x>√n,直接暴力!              
            {
                long long ans=0;
                for(int i=y;i<=n;i+=x) ans+=a[i];  //暴力枚举加和 
                printf("%lld
",ans);
            }
        } 
        else       //把第x个数改成y 
        {
            for(int i=1;i<=sqrt(n);i++)  //更新第x个数所涉及到的所有的池
                dp[i][x%i]+=y-a[x]; 
            a[x]=y;
        }
    } 
    return 0;
}