题目描述
There are (n) towns in Byteotia, connected with only (n-1) roads.
Each road directly links two towns.
All the roads have the same length and are two way.
It is known that every town can be reached from every other town via a route consisting of one or more (direct-link) roads.
In other words, the road network forms a tree.
Byteasar, the king of Byteotia, wants three luxury hotels erected to attract tourists from all over the world.
The king desires that the hotels be in different towns and at the same distance one from each other.
Help the king out by writing a program that determines the number of possible locations of the hotel triplet in Byteotia.
输入格式
The first line of the standard input contains a single integer nn ((1le nle 5 000)), the number of towns in Byteotia.
The towns are numbered from (1) to (n).
The Byteotian road network is then described in (n-1) lines.
Each line contains two integers (a) and (b) ((1le ale ble n)) , separated by a single space, that indicate there is a direct road between the towns (a) and (b).
输出格式
The first and only line of the standard output should contain a single integer equal to the number of possible placements of the hotels.
题意翻译
给定一棵树,在树上选 (3) 个点,要求两两距离相等,求方案数。
输入输出样例
输入
7
1 2
5 7
2 5
2 3
5 6
4 5
输出
5
Solution
一道经典的树形 (dp) 好题,做到就是赚到。
我们从题目限制条件开始分析:
题目要求选出三个点,使得它们两两距离相等,那么这三个点的位置差不多是这样的:
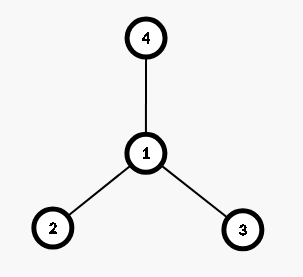
此时 ((2,3,4)) 就是符合条件的一组点。
从图中可以看出,这等价于三个点中深度较大的两点 ((2,3)) 的 (lca(1)) 到三点的距离相等。
这样的话,我们把这个 (lca) 拎出来当根,那么符合条件的三个点一定是同深度的。
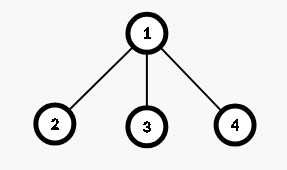
所以说,我们选定一个距离 (d),那么距离根为 (d) 的三个点有可能就是符合要求的点对。
为什么是有可能呢?因为这不能保证 (lca) 是根节点,所以我们要在根的不同的子树中选。也就是说,我们当前枚举的根节点的每条出边指向的点所在的子树上最多只能选一个点。
所以对于一个根节点,我们要枚举每一个子树,然后统计答案,因为要三个点,所以是当前子树中的个数乘上之前选过的里面选了 (2) 个点的情况数了。
状态设置
(f_2[i]) 表示整棵树之前遍历的部分中,深度为 (i) 的所有点中,选出两个点的合法方案数。
(f_1[i]) 表示整棵树之前遍历的部分中,深度为 (i) 的所有点中,选出一个点的合法方案数。
(num[i]) 表示以 (i) 为根的子树中,距离 (i) 为 (d) 的点有多少个。
状态转移
对于当前选三个点的情况,就是多了之前的子树里选两个点,当前子树里选一个点的情况。
对于当前选两个点的情况,就是多了之前的子树里选一个点,当前子树里选一个点的情况。
对于当前选一个点的情况,就是多了当前子树里所选的点的情况。
(ans+=f_2[d]*num[d])
(f_2[d]+=f_1[d]*num[d])
(f_1[d]+=num[d])
那么对于根的每一个子树,我们都 (dfs) 一遍求一下 (num) 数组,然后转移即可。
时间复杂度 (O(n^2))。
Code
#include<iostream>
#include<cstring>
#include<cstdio>
#define db double
#define ll long long
using namespace std;
inline int read()
{
char ch=getchar();
int a=0,x=1;
while(ch<'0'||ch>'9')
{
if(ch=='-') x=-x;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
a=(a<<1)+(a<<3)+(ch^48);
ch=getchar();
}
return a*x;
}
const int N=5005;
const int INF=1e9;
int n,Edge;
int head[N];
ll Max,ans,num[N],f1[N],f2[N];
struct node
{
ll to,nxt;
}a[N<<1];
void add(ll from,ll to)
{
Edge++;
a[Edge].to=to;
a[Edge].nxt=head[from];
head[from]=Edge;
}
void dfs(int u,int fa,ll dep) //求出深度为dep的点有几个
{
Max=max(Max,dep); //顺便求一下最大深度
num[dep]++;
for(int i=head[u];i;i=a[i].nxt)
{
int v=a[i].to;
if(v==fa) continue;
dfs(v,u,dep+1);
}
}
int main()
{
n=read();
for(int i=1;i<n;i++)
{
ll u=read();
ll v=read();
add(u,v);add(v,u);
}
for(int u=1;u<=n;u++)
{
memset(f1,0,sizeof(f1));
memset(f2,0,sizeof(f2));
for(int i=head[u];i;i=a[i].nxt)
{
int v=a[i].to;Max=0;
memset(num,0,sizeof(num));
dfs(v,u,1); //对于根的每一个子树,都要dfs求一下num
for(ll k=1;k<=Max;k++)
{
ans+=f2[k]*num[k]; //选三个点的情况多了前面选两个,当前选一个的情况
f2[k]+=f1[k]*num[k]; //选两个点的情况多了前面选一个,当前选一个的情况
f1[k]+=num[k]; //选一个点的情况多了当前选一个的情况
}
}
}
printf("%lld
",ans);
return 0;
}