P3478 [POI2008]STA-Station题解

P3478 [POI2008]STA-Station题解

原题面

知识点

• 换根DP

大致题意

给出一个 N 个点的树,找出一个点来,以这个点为根的树时,所有点的深度之和最大

分析

换根DP的模板题。

如果您还不会换根DP的话,可以先去看看UltiMadow巨佬的文章:

【日报#278】[学习笔记]换根dp,我一开始也是从那里学的qwq

这里我们设

• (size[i])为以(1)为根节点时节点(i)的子树大小

• (dep[i])为以(1)为根节点时节点(i)的深度大小

• (dp[i])为以(i)为根节点时深度之和的大小

很明显,我们可以通过一遍DFS求出以(1)为根节点时的深度之和

如果一个个的去算的话

照这个数据范围,显然会T飞

这个时候就要用到换根DP了

换根(DP)优化

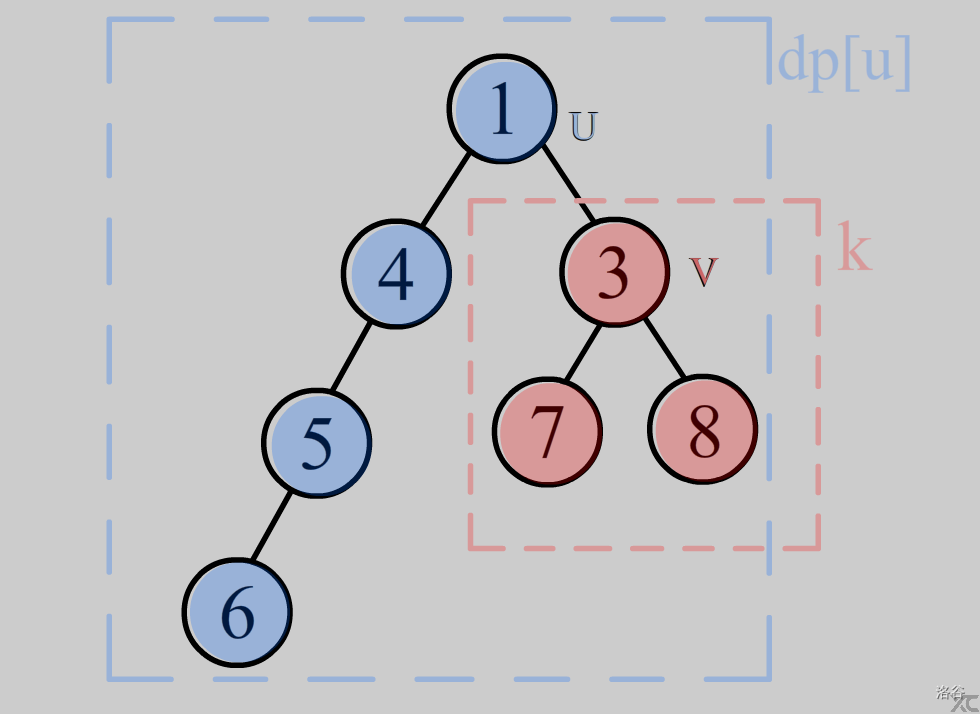
可以看出,当我们把根节点从1换到3时

对子节点3的贡献由两部分组成

1.自己子树的贡献(图中的k)

2.父亲节点(1)的贡献

---

如何转移

• 首先是(k),作为自己子树所产生的贡献肯定要加上

• (dp[u])为以(u)为根节点时的深度总值,在计算时,要减去(v)的子树所产生的贡献,不然就重复计算了,同时

在以 (u)为根时,v节点及其子树内的所有节点的深度都增加了(1),需要减去

(图中红色的节点)

合起来就是(dp[u]-(size[v]+k))

• 除v子树外的其他节点也一样

在以(v)为根时，除(v)节点及其子树外的其他节点的深度都增加了(1)

(图中蓝色的节点)

合起来就是((size[1]-size[v]))

得到转移方程

• (dp[v] = k+(dp[u]-(k+size[v]))+(size[1]-size[v]))

化简一下

• (dp[v] = dp[u]-2size[v]+size[1])

转移方程推出来了,代码部分就不难实现了,两遍dfs,一次dfs统计子树内的节点对当前节点的贡献
一次dfs换根

贴个代码：

#include<bits/stdc++.h>
using namespace std;
const int MAXN  = 100010;
long long dp[MAXN],dep[MAXN],size[MAXN];
int vis[MAXN];
vector <int> son[MAXN];
int n;

void dfs1(int x){
	size[x] = 1;
    vis[x] = 1;
	for(int i=0;i<son[x].size();i++){
		int v = son[x][i];
		if(!vis[v]){
		dep[v] = dep[x] +1;
		dfs1(v);
		size[x]+=size[v];	
		}
			
	}
}
void dfs2(int x){
    vis[x] = 1;
	for(int i=0;i<son[x].size();i++){
		int v = son[x][i];
		if(!vis[v]){
		dp[v] = dp[x] +size[1] - 2*size[v];
		dfs2(v);	
		}
	}
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<n;i++){
		int u,v;
		scanf("%d%d",&u,&v);
		son[u].push_back(v);
		son[v].push_back(u);
	}
	dfs1(1);
	
	for(int i=1;i<=n;i++) dp[1]+=dep[i];
	
	memset(vis,0,sizeof(vis));
	dfs2(1);
	long long ans = -0x3f;
	int jd =999;
	for(int i=1;i<=n;i++){
		if(ans < dp[i]) ans = dp[i], jd = i;
	}
	cout<<jd;
}