SP2713 GSS4 题解

SP2713 GSS4 题解

间隙

双倍经验

前置知识:线段树

如果您还不会线段树的话,推荐去看一下这篇文章,我一开始也是在那里学的

大致题意

给一堆数,有以下两个操作:

• 给出一个区间([L,R]),把该区间内的每个数都开平方

• 给出一个区间([L,R]),查询这个区间的每个数的和

分析

首先看一下这个数据范围,(1e18),直接暴力的话肯定会T飞

求和操作很简单,相信学过线段树的人应该都会

难点在于这个开方操作,我们没法像线段树模板那样打个懒标记来进行下传操作

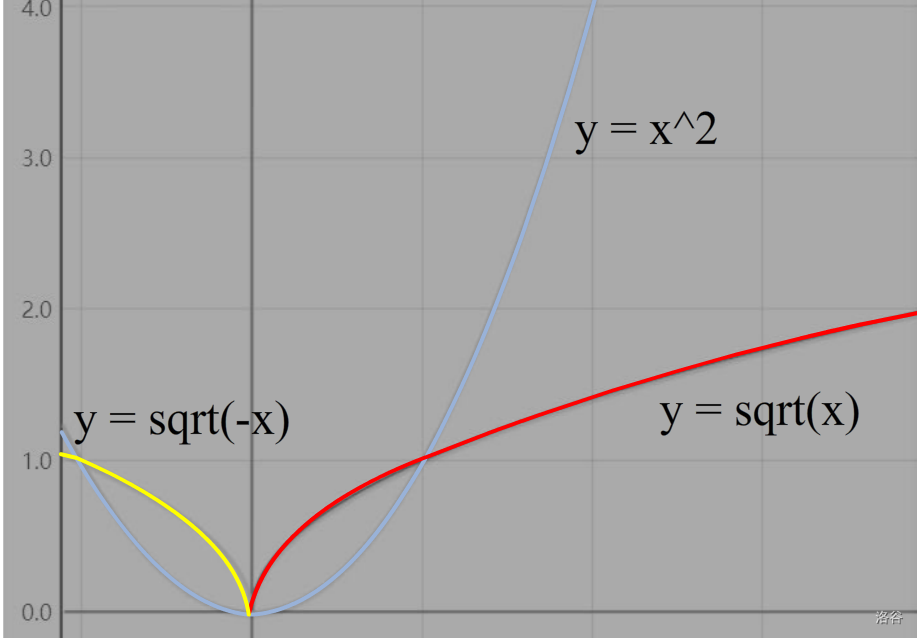
通过观察(sqrt x)函数图像缓慢的增长率或者其他性质不难发现,很多开方操作是不必要的,考虑减枝优化:

• 不难发现,当一个区间内的所有数都是(1)时,再对该区间进行开方操作对该区间内的总值造成不了任何改变((sqrt{1} = 1))

因此代码实现方面只要在区间内总值均为1的情况下加一个小剪枝即可

---

代码实现

思路理解了代码实现难度就不高了,但还是有几个坑点...具体的注释里有写

#include<bits/stdc++.h>
#define lson (node<<1)//左儿子
#define rson (node<<1|1)//右儿子
#define ll long long 
#define int long long //记得开long long
using namespace std;
const int MAXN = 100005;
struct st{
	int l,r;//左右端点
	ll sum;
}tree[MAXN<<2];

ll a[MAXN];
int n,m;
void pushup(int node){
	tree[node].sum = tree[lson].sum + tree[rson].sum;//合并操作
}
void build(int node,int l,int r){//建树
	tree[node].l = l;
	tree[node].r = r;
	if(l==r){
		tree[node].sum = a[l];
		return;
	}
	int mid = (l+r)>>1;
	build(lson,l,mid);
	build(rson,mid+1,r);
	pushup(node);
}
void change(int node,int l,int r){
	int L = tree[node].l,R = tree[node].r;
	if(tree[node].sum==R-L+1) return;//如果总和为区间长度,也就是所有值均为1时,直接剪枝掉
	if(L==R){
		tree[node].sum = sqrt(tree[node].sum);
		return;
	}
	int mid = (L+R)>>1;
	if(l<=mid){
			change(lson,l,r);
	}
	if(r>mid){
			change(rson,l,r);
	}
	pushup(node);
}
ll query(int node,int l,int r){//查询
	int L = tree[node].l,R = tree[node].r;
	if(l<=L&&r>=R){//包含在查询区间内,直接返回sum值
		return tree[node].sum;
	}
	int mid = (L+R)>>1;
	ll ans = 0;
	if(l<=mid){
		ans+=query(lson,l,r);
	}
	if(r>mid){
		ans+=query(rson,l,r);
	}
	return ans;
}
signed main(){
	ios::sync_with_stdio(false);//不加貌似会TLE?
    cin.tie(0);
    cout.tie(0);
	int Case=0;
	while(cin>>n){
	printf("Case #%d:
",++Case);//注意,样例里那个case是要输出的,一开始被这里卡了好久...
	memset(a,0,sizeof(a));//记得要先memset
	memset(tree,0,sizeof(tree));
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	build(1,1,n);
	cin>>m;
	while(m--){
		int mode,left,right;
		cin>>mode>>left>>right;
		if(left > right){
			swap(left,right);
		}
		if(mode==0){
			change(1,left,right);
		}
		else{
			printf("%lld
",query(1,left,right));
		}
	 }
	 puts("");//记得换行
	}
	
}