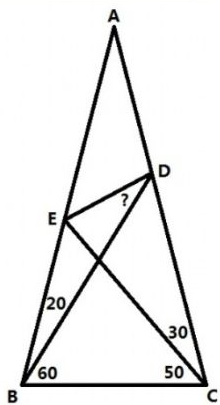
如图所示,
已知AB = AC,∠ABD = 20°,∠ACE = 30°,∠CBD = 50°,∠BCE = 60°
求∠BDE
看上去貌似是个初中级别的题,应该也有初中级别的解法,不过懒得去找|||- -
于是直接进行暴力求解
(1)
∠BAD = 180° - 80° - 80° = 20° =>
∠BAD = ∠ABD =>
AD = BD
(2)
∠BEC = 180° - 80° - 50° = 50° =>
∠BEC =∠BCE =>
BC = BE
(3)
为了简便起见,我们假设
AB = AC = m
另外,由于后续涉及到正弦和余弦计算,故统一改用弧度
∠ADB = π - π/9 - π/9 = 7π/9
设∠EDB = x, 则
∠BED = π - π/9 - x = 8π/9 - x
(4)
对三角形ABC使用正弦定理,可知
sin∠ABC / AC = sin∠BAC / BC
由于AC=m,故
BC = BE
= m * sin(π/9) / sin(4π/9)
(5)
对三角形ABD使用正弦定理,可知
sin∠ADB / AB = sin∠ABD / AD
由于AB = m,故
AD = BD
= m * sin(π/9) / sin(7π/9)
(6)
对三角形BDE使用正弦定理,可知
sin∠BDE / BE = sin∠BED / BD
结合(1)(2)(3)(4)(5),即可以得到
sin (x) / (m * sin(π/9) / sin(4π/9)) =
sin(8π/9 - x) / (m * sin(π/9) / sin(7π/9))
整理一下得到
sin(4π/9)* sin(x) = sin(7π/9)* sin(8π/9 - x)
再利用两角和公式把sin(8π/9 - x)展开,得到
sin(4π/9)* sin(x) = sin(7π/9)* (sin(8π/9)cos(x) - cos(8π/9)sin(x))
把sin(x)的项移到左边,cos(x)的项移到右边,得到
sin(x)* (sin(4π/9)+ cos(8π/9)) = cos(x)sin(7π/9)sin(8π/9)
tan(x) = sin(7π/9)sin(8π/9)/ (sin(4π/9)+ cos(8π/9))
(7)
如果此时直接把结果写成arctan XXX,貌似也不能算错。
不过在这个场景下,结果还可以继续化简。
tan(x) = sin(7π/9)sin(8π/9)/ (sin(4π/9)+ cos(8π/9))
= sin(π - 2π/9)sin(π - π/9)/ (sin(4π/9)+ sin(π - 2π/9)cos(π - π/9))
利用 sin(π - α)= sin(α),以及 cos(π - α)= - cos(α),可以得到
tan(x)= sin(2π/9)sin(π/9)/ (sin(4π/9)- sin(2π/9) cos(π/9))
(8)
以下需要用到一些小技巧,核心思想是把结果尽可能地用π/3或者π/6来表示,
由于π/3(60°)和π/6(30°)的正弦和余弦值是要求背出来的,就能达到化简的目的。
为了简便起见,令α = π/9,则
2α = 2π/9 = π/3 - π/9 = π/3 - α
4π/9 = π/3 + π/9 = π/3 + α
于是(7)中的式子化为:
tan(x)= sin(π/3 - α) sin(α)/ (sin(π/3 + α)- sin(π/3 - α)cos(α))
利用两角和公式将其展开,得到
tan(x)= (√3/2 * sin(α)cos(α)- 1/2 * sin^2(α)) / (√3/2 * cos(α)+ 1/2 * sin(α) - √3/2 * cos^2(α)+ 1/2 * sin(α) cos(α))
其中二次项sin^2(α)、cos^2(α)和 sin(α) cos(α),分别用降幂公式和二倍角公式化成2α形式,再用2α = π/3 - α去代换如下:
sin^2(α) = (1 - cos(2α))/ 2 = (1 - cos(π/3 - α))/ 2 = 1/2 - 1/4 * cos(α) - √3/4 * sin(α)
cos^2(α) = (1 + cos(2α))/ 2 = (1 + cos(π/3 - α))/ 2 = 1/2 + 1/4 * cos(α) + √3/4 * sin(α)
sin(α) cos(α) = sin(2α)/ 2 = sin(π/3 - α)/ 2 = √3/4 * cos(α)- 1/4 * sin(α)
把这三个结果代入,再合并同类项,得到
tan(x) = (3/8 * cos(α)- √3/8 * sin(α) - 1/4 + 1/8 * cos(α)+ √3/8 * sin(α)) / (√3/2 * cos(α)+ 1/2 * sin(α) - √3/4 - √3/8 * cos(α) - 3/8 * sin(α)+ √3/8 * cos(α) - 1/8 * sin(α))
= (1/2 * cos(α)- 1/4) / (√3/2 * cos(α)- √3/4)
= ((1/4) * (2 * cos(α)- 1)) / ((√3/4)*(2 * cos(α)- 1))
非常凑巧,这个除法式子里面,恰好可以上下同时约掉一个2 * cos(α)- 1
于是得到
tan(x) = 1/√3 = √3/3
稍微有点基础的同学们应该一眼就可以看出,
x = π/6 , 也就是30°
======================================================
小结:
此题主要的知识点有:
(1)最基本的初中几何知识;
(2)正弦定理;
(3)两角和公式,包括积化和差、和差化积、二倍角等;
(4)降幂公式;
(5)常见角(如π/3和π/6)的正弦、余弦、正切等值;
(6)遇到正弦、余弦不太好表示的角,想办法将其转化成与常见角的和差关系;