1028. 从先序遍历还原二叉树。 深搜

我们从二叉树的根节点 root 开始进行深度优先搜索。

在遍历中的每个节点处，我们输出 D 条短划线（其中 D 是该节点的深度），然后输出该节点的值。（如果节点的深度为 D，则其直接子节点的深度为 D + 1。根节点的深度为 0）。

如果节点只有一个子节点，那么保证该子节点为左子节点。

给出遍历输出 S，还原树并返回其根节点 root。

示例 1：

输入："1-2--3--4-5--6--7"
输出：[1,2,5,3,4,6,7]

示例 2：

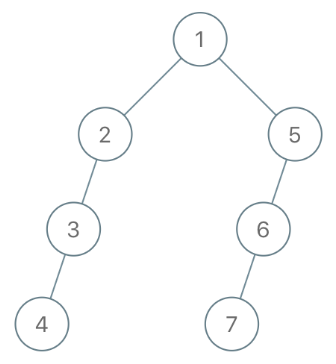
输入："1-2--3---4-5--6---7"
输出：[1,2,5,3,null,6,null,4,null,7]

示例 3：

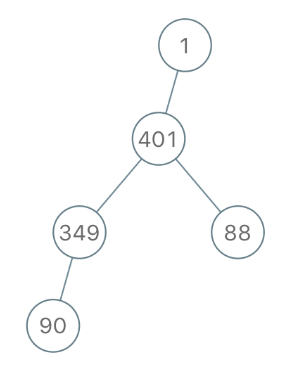
输入："1-401--349---90--88"
输出：[1,401,null,349,88,90]

提示：

原始树中的节点数介于 1 和 1000 之间。
每个节点的值介于 1 和 10 ^ 9 之间。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/recover-a-tree-from-preorder-traversal
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    string s;   //全局变量字符串
    int len;    //字符串长度
    int i = 0;  //全局变量下标
    int depth = 0;  //字符串中某一项的深度值，每次读取都是从0开始
    

    TreeNode* recoverFromPreorder(string str) {
        s = str;
        len = s.size();
        return dfs(0);
    }

    //td为当前节点深度
    TreeNode* dfs(int td) {
        //右移下标到下一项，每多移动一次，即该项深度+1
        while (i < len && s[i] == '-'){
            i++;
            depth++;
        }
        //若当前节点深度与字符串中项的深度不同，说明当前节点为空，返回空指针
        if (td != depth) return nullptr;
        //否则，计算字符串中当前项的值
        int val = 0;
        while (i < len && s[i] != '-'){
            val = val * 10 + s[i++] - '0';
        }
        //生成新的指针，继续进行递归
        TreeNode* root = new TreeNode(val);
        //令depth=0，因为字符串会根据-的数量，计算该节点的深度值
        depth = 0;
        root->left = dfs(td + 1);
        root->right = dfs(td + 1);

        return root;


    }
};